4 Funktio
Opetusvideot funktiosta
Funktio ja funktion kuvaaja
Funktion merkintöjä ja funktion arvon laskeminen
Funktion merkintöjä ja funktion arvon laskeminen
Esimerkkitehtävät
- Laske funktion [[$ f(x) =6x-3 $]] arvo muuttujan arvoilla [[$ x = 1 $]], [[$ x=0 $]] ja [[$ x=-2 $]].
- Millä muuttujan [[$ x $]] arvolla funktio [[$ f(x)=6x-3 $]] saa arvon a) [[$ 9 $]] ? b) [[$ 0 $]] ?
- Kuvassa on funktioiden f ja g kuvaajat.
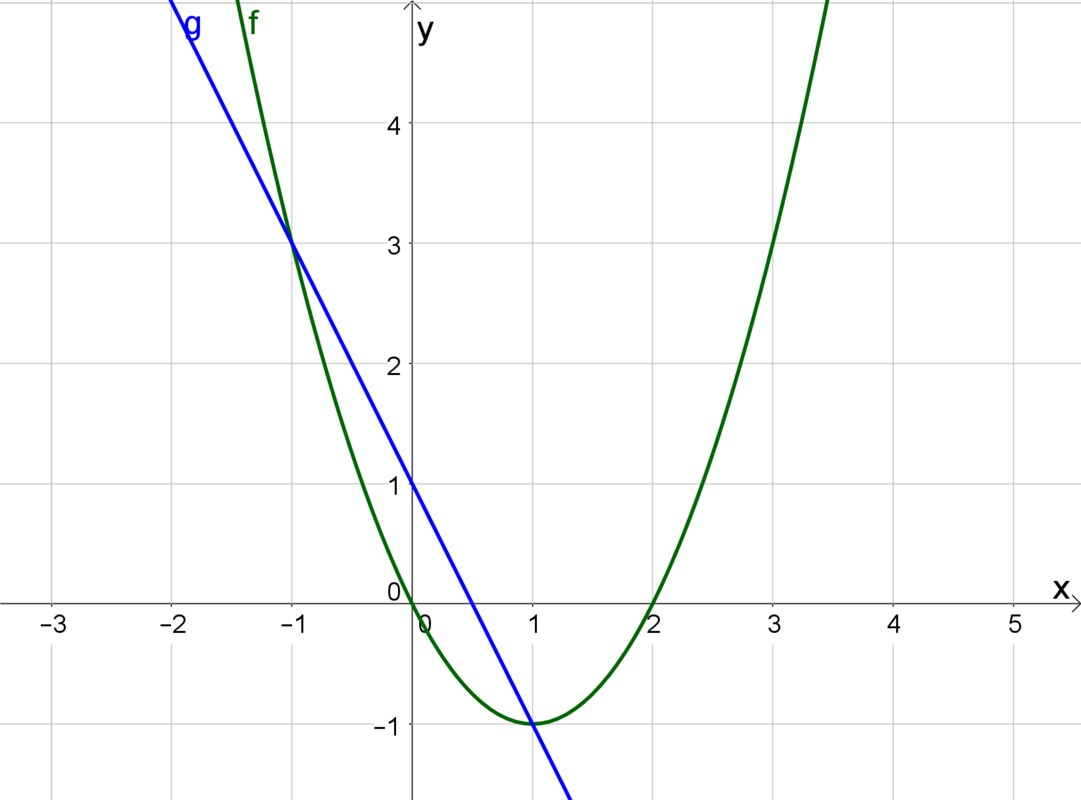
Päättele kuvasta:
- funktion f arvo kohdassa [[$ x = 1 $]]
- funktion f nollakohdat
- funktion g arvo kohdassa [[$ x = 3 $]] ja [[$ x = 0 $]]
- funktioiden f ja g leikkauspisteet
- millä muuttujan [[$ x $]] arvolla funktio f saa positiivisia arvoja?
1. [[$ f(1)= 3 , f(0)=-3 \text{ ja } f(-2) = -15 $]]
2. [[$ a) \quad x = 2 \\ \\ b) \quad x = -\frac{1}{2} $]]
3. [[$ f (1) =-1 \\ \\ \text{Nollakohdat } x = 0 \text{ ja } x = 2 \\ \\ g(3) = \text{ ei voi päätellä kuvasta, } g(0) = 1 \\ \\ \text{Leikkauspisteet } x = -1 \text{ ja } x =1 \\ \\ f(x) > 0 \text{ , kun } x<0 \text{ tai } x > 2 $]]
Funktio, teoriaa
Funktio on sääntö, joka kertoo, millä menetelmällä jostakin luvusta saadaan uusi luku.
Esim.1: Sääntö luku kerrotaan kahdella ja sitten lisätään 5 kuvaa funktiota
[[$$ f(x) = 2x+5 $$]]
Tässä:
Esim.2. jos muuttujalle annetaan arvo [[$ x = 2 $]], saadaan laskettua funktion arvo: [[$ f(2)=2 \cdot 2+5 = 9. $]]
Kun funktion arvo tunnetaan ja kysytään missä kohtaa se saadaan:
Esim. 3. Missä kohdassa funktio saa arvon 3? (kohta = x).
Ratkaisu: [[$$ 2x+5 = 3 \\ 2x=3-5 \\ 2x = -2 \\ x = -1 $$]]
Funktion kuvaaja:
Miten esimerkit näkyvät funktion kuvaajalla koordinaatistossa:
Kohta=x, arvo = y
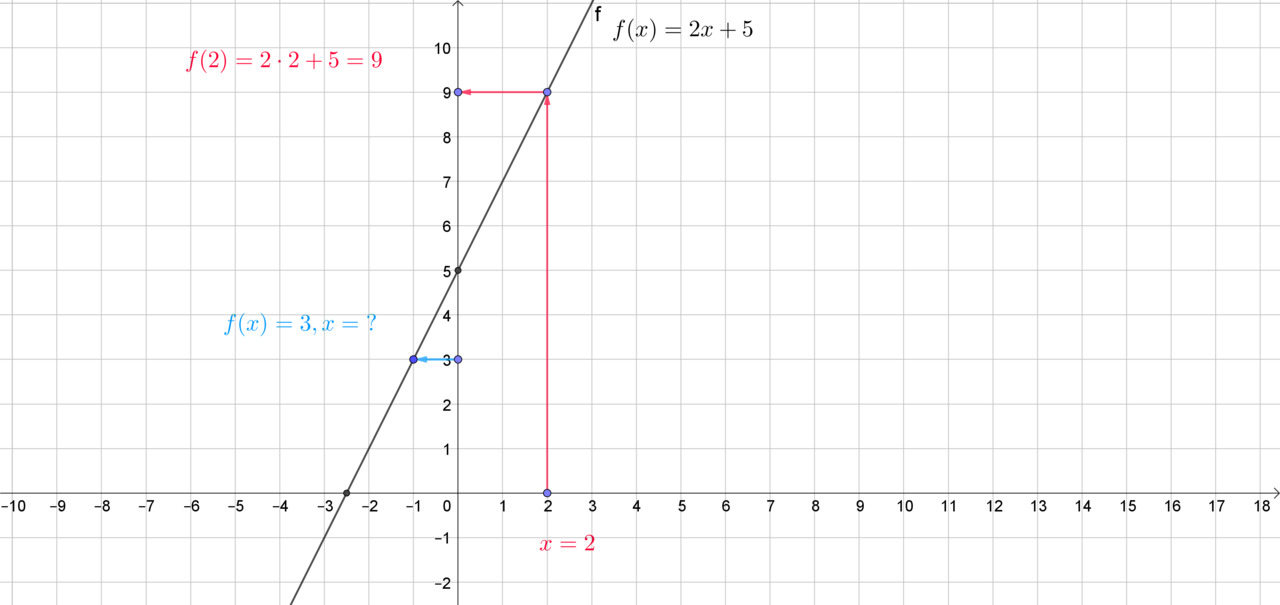
Funktion nollakohta tarkoittaa sitä kohtaa, jossa funktion arvo on nolla; nollakohdassa funktion kuvaaja leikkaa [[$ x $]]-akselin.
Esim. 4: Mikä on funktion [[$ g(x) = 2^x-8 $]] nollakohta?
Ratkaisu: [[$$ 2^x-8=0 \\ 2^x = 8 \\ 2^x = 2^3 \\ x=3. $$]]
Kuvaajan piirtäminen:
Esim. 5. Piirrä funktion [[$ f(x) = 2^x $]] kuvaaja laskemalla pisteitä, jotka kuuluvat kuvaajalle. Harjoittele myös symbolisella laskimella.
Ratkaisu: Taulukoidaan x ja y arvoja, kun [[$ y = 2^x $]]:
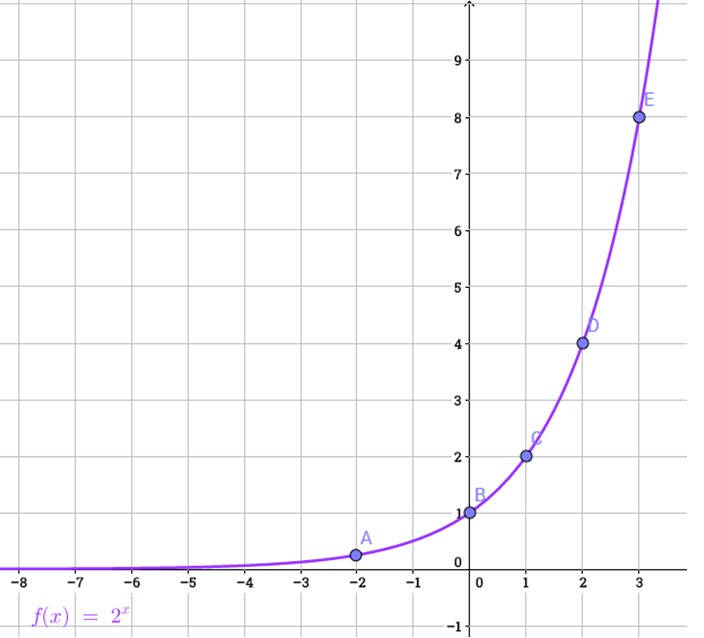
Esim.1: Sääntö luku kerrotaan kahdella ja sitten lisätään 5 kuvaa funktiota
[[$$ f(x) = 2x+5 $$]]
Tässä:
- [[$ f $]]on funktion nimi
- [[$ x $]] on muuttuja
- [[$ 2x+5 $]] on funktion lauseke.
Esim.2. jos muuttujalle annetaan arvo [[$ x = 2 $]], saadaan laskettua funktion arvo: [[$ f(2)=2 \cdot 2+5 = 9. $]]
Kun funktion arvo tunnetaan ja kysytään missä kohtaa se saadaan:
Esim. 3. Missä kohdassa funktio saa arvon 3? (kohta = x).
Ratkaisu: [[$$ 2x+5 = 3 \\ 2x=3-5 \\ 2x = -2 \\ x = -1 $$]]
Funktion kuvaaja:
Miten esimerkit näkyvät funktion kuvaajalla koordinaatistossa:
Kohta=x, arvo = y

Funktion nollakohta tarkoittaa sitä kohtaa, jossa funktion arvo on nolla; nollakohdassa funktion kuvaaja leikkaa [[$ x $]]-akselin.
Esim. 4: Mikä on funktion [[$ g(x) = 2^x-8 $]] nollakohta?
Ratkaisu: [[$$ 2^x-8=0 \\ 2^x = 8 \\ 2^x = 2^3 \\ x=3. $$]]
Kuvaajan piirtäminen:
Esim. 5. Piirrä funktion [[$ f(x) = 2^x $]] kuvaaja laskemalla pisteitä, jotka kuuluvat kuvaajalle. Harjoittele myös symbolisella laskimella.
Ratkaisu: Taulukoidaan x ja y arvoja, kun [[$ y = 2^x $]]:
| x | y | Piste (x,y) |
| -2 | 1/4 | (-2,1/4) |
| 0 | 1 | (0,1) |
| 1 | 2 | (1,2) |
| 2 | 4 | (2,4) |
| 3 | 8 | (3,8) |
