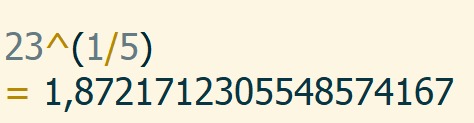
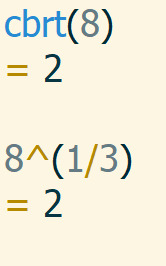2.4 Potenssiyhtälö
Potenssin ratkaiseminen ja neliöjuuri
Esimerkkikysymykset
1. Ratkaise yhtälö
[[$ \quad $]] a) [[$ x^2=16 $]]
[[$ \quad $]] b) [[$ x^3=125 $]]
[[$ \quad $]] c) [[$ x^4=81 $]]
2. Määritä luvun
[[$ \quad $]] a) 100 neliöjuuri
[[$ \quad $]] b) 27 kuutiojuuri
[[$ \quad $]] c) 8 kuutio
[[$ \quad $]] a) [[$ x^2=16 $]]
[[$ \quad $]] b) [[$ x^3=125 $]]
[[$ \quad $]] c) [[$ x^4=81 $]]
2. Määritä luvun
[[$ \quad $]] a) 100 neliöjuuri
[[$ \quad $]] b) 27 kuutiojuuri
[[$ \quad $]] c) 8 kuutio
Ratkaisut esimerkkikysymyksiin
1. a) [[$ x^2=16 \\x=\pm \sqrt{16}=\pm 4$]]
b) [[$ x^3=125 \\x=\sqrt[3]{125}=5 $]]
c) [[$ x^4=81 \\ x=\pm \sqrt[4]{81}=\pm 3 $]]
2. a) Luvun 100 neliöjuuri on [[$ \sqrt{100}=10 $]].
b) Luvun 27 kuutiojuuri on [[$ \sqrt[3]{27}=3 $]].
c) Luvun 8 kuutio on [[$ 8^3=512 $]].
b) [[$ x^3=125 \\x=\sqrt[3]{125}=5 $]]
c) [[$ x^4=81 \\ x=\pm \sqrt[4]{81}=\pm 3 $]]
2. a) Luvun 100 neliöjuuri on [[$ \sqrt{100}=10 $]].
b) Luvun 27 kuutiojuuri on [[$ \sqrt[3]{27}=3 $]].
c) Luvun 8 kuutio on [[$ 8^3=512 $]].
Perustehtävät
P1. Tutki sijoittamalla, onko a) [[$ x=2 $]] b) [[$ x=-2 $]] yhtälön [[$ x^2=4 $]] ratkaisu.
P2. Tutki sijoittamalla, onko a) [[$ x=4 $]] b) [[$ x=-4 $]] yhtälön [[$ x^3=64 $]] ratkaisu.
P3. Ratkaise yhtälö ilman laskinta.
a) [[$ x^2=49 $]]
b) [[$ x^5=1 $]]
c) [[$ x^3=-8 $]]
P4. Lukua kerrottiin itsellään neljästi ja tulosta vähennettiin luku 1. Lopputulos oli 15. Mikä oli alkuperäinen luku?
P2. Tutki sijoittamalla, onko a) [[$ x=4 $]] b) [[$ x=-4 $]] yhtälön [[$ x^3=64 $]] ratkaisu.
P3. Ratkaise yhtälö ilman laskinta.
a) [[$ x^2=49 $]]
b) [[$ x^5=1 $]]
c) [[$ x^3=-8 $]]
P4. Lukua kerrottiin itsellään neljästi ja tulosta vähennettiin luku 1. Lopputulos oli 15. Mikä oli alkuperäinen luku?
Syventävät tehtävät
P5. Määritä luvun 81 a) neliöjuuri b) neliö.
P6. Ratkaise yhtälö ilman laskinta.
a) [[$ x^2=-16 $]]
b) [[$ x^3=-125 $]]
c) [[$ 4x^4=40000 $]]
P7. Pankkitilille talletetaan 400 €. 20 vuoden kuluttua sijoituksen arvo on kaksinkertaistunut. Mikä tilin vuotuinen korkoprosentti?
P8. Määritä logaritmin kantaluku [[$ k>0 $]] seuraavissa yhtälöissä.
a) [[$ \log_k 144=2 $]]
b) [[$ \log_k 625 = 4 $]]
P6. Ratkaise yhtälö ilman laskinta.
a) [[$ x^2=-16 $]]
b) [[$ x^3=-125 $]]
c) [[$ 4x^4=40000 $]]
P7. Pankkitilille talletetaan 400 €. 20 vuoden kuluttua sijoituksen arvo on kaksinkertaistunut. Mikä tilin vuotuinen korkoprosentti?
P8. Määritä logaritmin kantaluku [[$ k>0 $]] seuraavissa yhtälöissä.
a) [[$ \log_k 144=2 $]]
b) [[$ \log_k 625 = 4 $]]
Tehtävien vastaukset
Perustehtävät
P1.
Molemmat ovat ratkaisuja
P2.
Vain a) kohta toteuttaa yhtälön.
P3.
[[$ a) x = 7 \text{ tai } x = -7 \\ b) x= 1 \\ c) x=-2 $]]
P4. [[$ x = 2 \text{ tai } x = -2 $]]
Syventävät tehtävät
P5. [[$ a) 9 \\ b) 6561 $]]
P6. a) ei ratkaisua [[$ b) x = -5 \\ c) x = 10 \text{ tai } x=-10 $]]
P7. Vuotuinen korkoprosentti on 3,52 %.
P8. [[$ a) k = 12 \\ b) k = 5 $]]
P1.
Molemmat ovat ratkaisuja
P2.
Vain a) kohta toteuttaa yhtälön.
P3.
[[$ a) x = 7 \text{ tai } x = -7 \\ b) x= 1 \\ c) x=-2 $]]
P4. [[$ x = 2 \text{ tai } x = -2 $]]
Syventävät tehtävät
P5. [[$ a) 9 \\ b) 6561 $]]
P6. a) ei ratkaisua [[$ b) x = -5 \\ c) x = 10 \text{ tai } x=-10 $]]
P7. Vuotuinen korkoprosentti on 3,52 %.
P8. [[$ a) k = 12 \\ b) k = 5 $]]