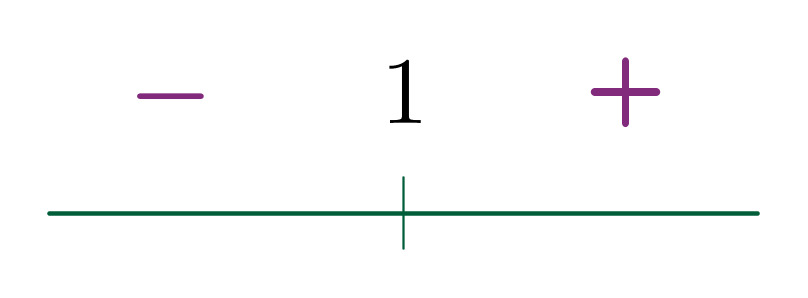5.2 Merkkikaavio
Merkkikaavio
Epäyhtälön ratkaisemisessa merkkikaavio on tärkeä, etenkin korkeamman asteen epäyhtälöissä.
Funktion merkki [[$ + $]] tai [[$ - $]] kertoo, ovatko funktion saamat arvot positiivisia vai negatiivisia.
Funktion arvo on positiivinen, kun kuvaaja on [[$ x $]]-akselin yläpuolella.
Vastaavasti funktion arvo on negatiivinen, kun kuvaaja on [[$ x $]]-akselin alapuolella.
[[$ xy $]]-koordinaatistossa funktion [[$ f(x) $]] arvo on sama kuin [[$y$]]:n arvo, koska [[$y=f(x)$]].
[[$ f(x) $]] on positiivinen eli [[$ f(x)>0 $]], kun [[$ y>0 $]].
Vastaavasti [[$ f(x) $]] on negatiivinen eli [[$ f(x)<0 $]], kun [[$ y<0 $]].
[[$ f(x) $]] on nolla eli [[$ f(x)=0 $]] niissä pisteissä, joissa funktion kuvaaja leikkaa tai sivuaa [[$ x $]]-akselia.
Jos [[$ f(x)<0 $]], nollakohta ei tule mukaan.
Jos [[$ f(x) \leq 0$]], nollakohta kuuluu mukaan.
Funktion merkki voi vaihtua ainoastaan silloin, kun ohitetaan funktion nollakohta. Merkki ei vaihdu nollakohdassa, jos funktion kuvaaja vain sivuaa [[$ x $]]-akselia nollakohdassa, kuten alla olevassa kuviossa.
Merkkikaavion laatiminen
Merkkikaavion pystyy laatimaan, vaikka ei tietäisi mikä funktio on kyseessä, jos sen kuvaaja ja nollakohdat ovat tiedossa.
Merkkikaavion laatiminen
- Määritetään funktion nollakohdat eli ne muuttujan [[$x$]] arvot, joissa funktion kuvaaja leikkaa [[$x$]]-akselin, laskemalla funktion lausekkeesta. Toinen vaihtoehto, mutta epätarkka, on katsoa nollakohdat kuvaajasta
- Jos nollakohtia on useampia, ne pitää kaikki määrittää.
- Merkkikaavioon ei tarvitse piirtää [[$x$]]-akselia, vaan riittää suora viiva, johon merkitään kaikki nollakohdat suuruusjärjestyksessä.
- Nollakohtien väliin merkitään joko [[$+$]] tai [[$-$]] sen mukaan, saako funktio kyseisellä välillä positiivisia vai negatiivisia arvoja. Kun funktion arvo on positiivinen, merkkikaavioon merkitään [[$+$]]. Kun funktion arvo on negatiivinen, merkkikaavioon merkitään [[$-$]].
- Jos kyseessä on toisen tai korkeamman asteen funktio, niin merkkikaavioon voi tulla useampia rivejä. Alimman rivin eli tulorivin merkit saadaan tulon tai osamäärän merkkisäännön avulla.
- Epäyhtälön ratkaisu luetaan tuloriviltä.
Merkkikaavion oikeellisuuden voi tarkistaa sijoittamalla nollakohtien välissä olevia muuttujan [[$ x $]] arvoja alkuperäiseen funktion lausekkeeseen ja katsomalla, täsmääkö tulos merkkikaavion kanssa.
Merkkikaavion tuloriviä merkittäessä on muistettava seuraavaa:
| 1. termin merkki | 2. termin merkki | tulo |
|---|---|---|
| [[$+$]] | [[$+$]] | [[$+$]] |
| [[$-$]] | [[$-$]] | [[$+$]] |
| [[$+$]] | [[$-$]] | [[$-$]] |
| [[$-$]] | [[$+$]] | [[$-$]] |
Esimerkiksi
[[$ -1\cdot(-1)=1\\1\cdot(-1)=-1\\-1\cdot1=-1 $]]
Tulo on negatiivinen, kun negatiivisten tulontekijöiden lukumäärä on pariton.
Tulo on positiivinen, kun negatiivisten tulontekijöiden lukumäärä on parillinen.
Esimerkiksi
[[$ -1\cdot(-1)\cdot(-1)=-1\\-1\cdot(-1)\cdot(-1)\cdot(-1)=1\\-1\cdot(-1)\cdot(-1)\cdot(-1)\cdot(-1)=-1 $]]
Ensimmäisen asteen polynomin merkkikaavio
Ensimmäisen asteen funktiolla [[$ f(x)=ax+b $]] ([[$ a \neq0 $]]) on yksi nollakohta.
Jos [[$ a>0 $]], kuvaaja on nouseva suora.
Jos [[$ a<0 $]], kuvaaja on laskeva suora.
Jos [[$ a=0 $]], funktio ei ole ensimmäisen asteen funktio, vaan vakiofunktio [[$ f(x)=b $]]. Tällöin sillä ei ole nollakohtaa (ellei ole [[$b=0$]]) ja kuvaaja on vaakasuora suora.
Esimerkki 1
Funktion [[$ f(x)=3 $]] kuvaaja on vaakasuora suora.
Yllä oleva vakiofunktio saa kaikilla muuttujan [[$ x $]] arvoilla positiivisen arvon [[$ 3 $]].
Esimerkki 2
a) Millä muuttujan [[$ x $]] arvoilla funktion kuvaaja on [[$ x $]]-akselini) yläpuolella
ii) alapuolella?
b) Ilmoita kuviossa funktion merkin vaihtelu.
c) Laadi merkkikaavio.
Ratkaisu:
a) Funktion kuvaaja on [[$ x $]]-akselin yläpuolella, kun [[$ x > 2 $]] eli kuvion oranssilla osuudella.
Funktion kuvaaja on [[$ x $]]-akselin alapuolella, kun [[$ x<2 $]] eli kuvion vihreällä osuudella.
b) Funktion merkki on oranssilla alueella [[$ + $]] ja vihreällä alueella [[$ - $]].
c) Merkkikaavio:
Esimerkki 3
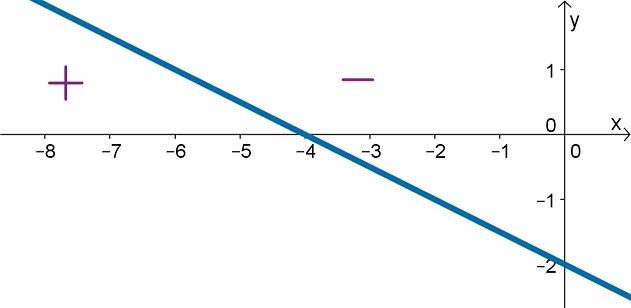
Laadi oheisen funktion merkkikaavio.
Ratkaisu:
Funktion kuvaaja on [[$ x $]]-akselin yläpuolella, kun [[$ x<-4 $]]. Vastaavasti kuvaaja on [[$ x $]]-akselin alapuolella, kun [[$ x>-4 $]]. Tällöin funktio saa positiivisia arvoja, kun [[$ x<-4 $]] ja negatiivisia arvoja, kun [[$ x>-4 $]].
Vastaus: Merkkikaavio:
Ensimmäinen aste, esimerkkejä
Esimerkki 4
Määritä funktion [[$ f(x)=-3x+4 $]] merkkikaavio.
Ratkaisu:
Ratkaistaan ensin funktion nollakohta.
[[$$ \begin{align}-3x+4&=0&∥-4\\-3x&=-4&∥:(-3)\\x&=\frac{4}{3}\end{align} $$]]
Nollakohta on [[$ x=\frac{4}{3} $]].
Koska funktion [[$-3x+4 $]] ensimmäisen asteen termin kerroin [[$ a $]] on negatiivinen ([[$ a=-3 $]]), funktion kuvaaja on laskeva suora ja funktio saa positiivisia arvoja, kun [[$ x<\frac{4}{3} $]].
Merkkikaavio:
GeoGebra-sovelma 1. asteen funktiosta
Nollakohdan saat näkyviin klikkaamalla kohtaa "näytä nollakohta".
Kohdasta "näytä merkki" tulee funktion merkki näkyviin ja "näytä merkkikaavio" -valinnasta näet kyseisen funktion merkkikaavion.
Suora näkyy punaisena, kun funktio saa positiivisia arvoja ja sinisenä, kun funktio saa negatiivisia arvoja.
Mikä on funktion merkki, kun [[$ a=0 $]] ja [[$ b<0 $]]?
Mikä on funktion merkki, kun [[$ a=0 $]] ja [[$ b>0 $]]?
Toisen asteen polynomin merkkikaavio
Jos [[$ a>0 $]], paraabeli aukeaa ylöspäin.
Jos [[$ a<0$]], paraabeli aukeaa alaspäin.Tyyppikuvaaja on pelkistetty kuva funktion kuvaajasta, se tehdään yleensä ensimmäisen tai toisen asteen funktiosta.
Esimerkki 5
a) Millä muuttujan [[$ x $]] arvoilla funktion kuvaaja on
i) [[$ x $]]-akselin yläpuolella
ii) [[$ x $]]-akselin alapuolella?
b) Laadi merkkikaavio.
Ratkaisu:
Funktion kuvaaja on ylöspäin aukeava paraabeli.
Vastaus:
a) funktion kuvaaja on [[$ x $]]-akselin yläpuolella, kun [[$ x<-1 $]] tai [[$ x>8 $]],
funktion kuvaaja on [[$ x $]]-akselin alapuolella, kun [[$ -1<x<8 $]]
b) nollakohtien ja paraabelin aukeamissuunnan perusteella saadaan merkkikaavio:
Esimerkki 6
Laadi merkkikaavio funktiolle [[$f(x)=-3x^2+6$]].
Ratkaisu:
Määritetään funktion [[$f(x)=-3x^2+6$]] nollakohdat.
[[$-3x^2+6=0$]], kun [[$x= \pm \sqrt{2}$]]
Funktion [[$-3x^2+6$]] kuvaaja on alaspäin aukeava paraabeli.
Merkkikaavio:
Esimerkki 7
Piirrä kuvaaja sellaiselle funktiolle, joka toteuttaa seuraavat ehdot:
[[$ f(x)>0 $]], kun [[$ 1<x<4 $]], muulloin [[$ f(x)≤0 $]].
Ratkaisu:
Funktion nollakohdat ovat [[$ x=1 $]] ja [[$ x=4 $]], koska funktion merkki vaihtuu kyseisissä kohdissa.
Merkitään lukusuoralle nollakohdat.
Merkitään nollakohtien väliin [[$ + $]] tai [[$ - $]] sen mukaan, saako funktio kyseisessä kohdassa positiivisia vai negatiivisia arvoja.
Merkkikaavio kyseiselle funktiolle:
Vastaus:
Eräs vaihtoehto funktion kuvaajalle:
Lähtötietojen perusteella kuvaajan tarkkaa muotoa ei tiedetä. Kuvaaja voisi olla myös seuraavanlainen:
GeoGebra-sovelma toisen asteen funktiosta
Oheisella sovelmalla voit tutkia toisen asteen funktion merkkiä, kun muutat liukuja [[$ a $]],[[$ b $]] ja [[$ c $]].
Paraabeli näkyy vihreänä, kun [[$ f(x)>0 $]] ja sinisenä, kun [[$ f(x)<0 $]].
Huomaatko, miten merkkikaavio ja funktion merkki liittyvät toisiinsa?
Kolmannen asteen polynomin merkkikaavio
Kolmannen asteen polynomin [[$ ax^3+bx^2+cx+d $]] kolmannen asteen termin kerroin [[$ a $]] ilmoittaa funktion kuvaajan suunnan.
Jos [[$ a>0 $]], muuttujan [[$ x $]] lähestyessä ääretöntä funktion kuvaaja lähestyy ääretöntä, kuten oheisessa kuviossa.
Jos [[$ a<0 $]], muuttujan [[$ x $]] lähestyessä ääretöntä funktion kuvaaja lähestyy miinus-ääretöntä, kuten oheisessa kuviossa.
Kolmannen asteen polynomin merkkikaavio
Kolmannen asteen polynomin merkkikaavio muodostetaan samalla periaatteella kuin edellä on tehty. Merkkikaavioon nollakohdat pitää kirjoittaa suuruusjärjestyksessä.
Esimerkki 8
Ohessa on erään kolmannen asteen polynomin kuvaaja. Laadi polynomin merkkikaavio.
Ratkaisu:
Polynomilla on vain yksi nollakohta [[$ x=1 $]]. Funktio saa negatiivisia arvoja, kun [[$ x<1 $]] ja positiivisia arvoja, kun [[$ x>1 $]].
Merkkikaavio:
Esimerkki 9
Ohessa on erään kolmannen asteen polynomin kuvaaja. Laadi polynomin merkkikaavio.
Ratkaisu:
Funktion nollakohdat ovat [[$ x=2$]], [[$ x=4 $]] ja [[$ x=8 $]]. Funktio saa positiivisia arvoja, kun [[$ 2<x<4 $]] tai [[$ x>8 $]]. Funktio saa negatiivisia arvoja, kun [[$ x<2 $]] tai [[$ 4<x<8 $]].
Merkkikaavio:
GeoGebra-sovelma 3. asteen funktiosta
Korkeampi aste, esimerkkejä
Esimerkki 10
Ohessa on erään kolmannen asteen polynomin kuvaaja. Laadi polynomin merkkikaavio.
Ratkaisu:
Funktion nollakohdat ovat [[$ x=-1 $]] ja [[$ x=2 $]]. Funktio saa positiivisia arvoja, kun [[$ x>2 $]].
Funktio saa negatiivisia arvoja, kun [[$ x<-1 $]] tai [[$ -1<x<2 $]] (toinen vaihtoehto ilmoittaa negatiiviset arvot: [[$ x<2 $]] ja [[$ x \neq -1 $]]).
Merkkikaavio:
Epäyhtälön pystyy ratkaisemaan funktion kuvaajan avulla, vaikka ei tietäisi, mikä funktio on kyseessä. Jos tietää funktion kuvaajan ja nollakohdat, voi päätellä, milloin epäyhtälö toteutuu.
Merkkikaavion ja kuvaajan perusteella voidaan kirjoittaa ylläolevalle polynomille epäyhtälön [[$ f(x)<0 $]] vastaus.
Funktion kuvaaja on [[$ x $]]-akselin alapuolella, kun [[$ x<-1 $]] tai [[$ -1<x<2 $]].
Vastaus: [[$f(x)<0$]], kun [[$ x<-1 $]] tai [[$ -1<x<2 $]]
Esimerkki 11
Laadi merkkikaavio oheiselle 5. asteen polynomille, jonka nollakohdat ovat [[$x=-\text{1,7}$]], [[$x=-\text{0,9}$]], [[$x=\text{0,8}$]], [[$x=3$]] ja [[$x=\text{4,3}$]].
Ratkaisu:
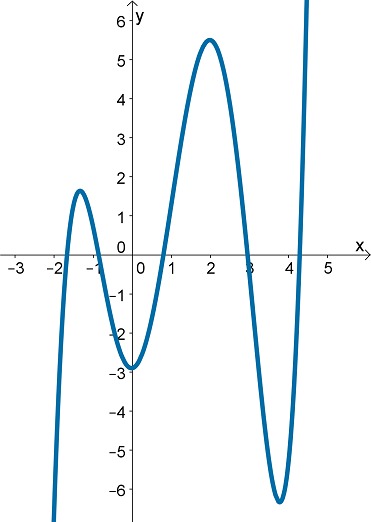
Funktio saa positiivisia arvoja, kun [[$-\text{1,7}<x<-\text{0,9}$]], [[$\text{0,8}<x<3$]] ja [[$x>\text{4,3}$]] . Funktio saa negatiivisia arvoja, kun [[$x<-\text{1,7}$]], [[$-\text{0,9}<x<\text{0,8}$]] ja [[$3<x<\text{4,3}$]].
Merkkikaavio:
GeoGebra-sovelma korkeamman asteen funktiosta
- Jos [[$a=0$]], on kyseessä 3. asteen funktio.
- Jos [[$a=0$]] ja [[$b=0$]], on kyseessä 2. asteen funktio.
- Jos [[$a=0$]], [[$b=0$]] ja [[$c=0$]], on kyseessä 1. asteen funktio.
