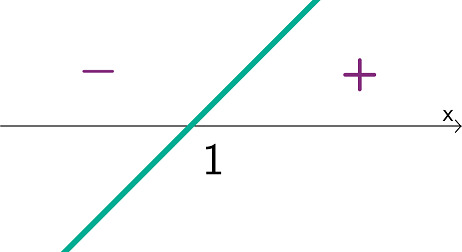*5.6 Murtoepäyhtälö

Murtoepäyhtälö

Murtoepäyhtälö pyritään saattamaan muotoon

[[$$ \dfrac{P(x)}{Q(x)} < 0 $$]][[$$ \dfrac{P(x)}{Q(x)} \leq 0 $$]][[$$ \dfrac{P(x)}{Q(x)} > 0 $$]][[$$ \dfrac{P(x)}{Q(x)} \geq 0 $$]][[$$ \dfrac{P(x)}{Q(x)} \neq 0 $$]]

Edellä [[$P(x)$]] ja [[$Q(x)$]] ovat polynomeja.

Murtoepäyhtälöä ratkaistaessa on aina aluksi selvitettävä määrittelyjoukko: nimittäjä ei saa olla nolla eli [[$Q(x) \neq 0$]].

Murtoepäyhtälön ratkaiseminen

Selvitetään epäyhtälön määrittelyehdot: nimittäjä ei saa olla nolla
Siirretään kaikki termit epäyhtälömerkin vasemmalle puolelle. Tällöin epäyhtälömerkin oikealle puolelle jää vain nolla
Sievennetään epäyhtälö niin pitkälle kuin mahdollista
Ratkaistaan osoittajan ja nimittäjän nollakohdat
Tutkitaan osoittajan ja nimittäjän merkki määrittelyalueella
Laaditaan merkkikaavio
Luetaan merkkikaaviosta epäyhtälön ratkaisu. Huomioidaan määrittelyehdot!

Murtoepäyhtälöä ratkaistaessa on muistettava, että epäyhtälöä kerrottaessa (tai jaettaessa) muuttujan sisältävällä lausekkeella pitäisi tietää lausekkeen merkki. Jos lauseke on negatiivinen, epäyhtälömerkin suunta on käännettävä.

Osamäärä on positiivinen, jos osoittaja ja nimittäjä ovat samanmerkkiset.
Osamäärä on negatiivinen, jos osoittaja ja nimittäjä ovat erimerkkiset.
Osamäärä on nolla, jos osoittaja on nolla.

osoittajan merkki	nimittäjän merkki	osamäärä
[[$+$]]	[[$+$]]	[[$+$]]
[[$-$]]	[[$-$]]	[[$+$]]
[[$+$]]	[[$-$]]	[[$-$]]
[[$-$]]	[[$+$]]	[[$-$]]

Esimerkki 1

Ratkaise murtoepäyhtälö [[$\dfrac{(4x-1)(x-1)}{x^2+1}<0$]].

Ratkaisu:
Määrittelyehto: Nimittäjä [[$x^2+1$]] on aina [[$>0$]], joten määrittelyjoukko on [[$\mathbb{R}$]]. Koska nimittäjä on aina positiivinen, epäyhtälön merkki riippuu vain osoittajasta.

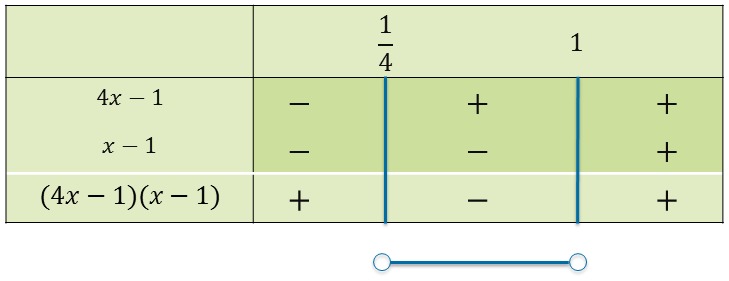
Tutkitaan binomien [[$4x-1$]] ja [[$x-1$]] merkkiä.
[[$$ \begin{align}4x-1&=0& \parallel &+1\\4x&=1& \parallel &:4\\x&=\frac{1}{4} \end{align} $$]]
[[$$ \begin{align}x-1&=0& \parallel +1\\x&=1 \end{align} $$]]

Binomin [[$4x-1$]] kuvaaja on nouseva suora.
Binomin [[$x-1$]] kuvaaja on nouseva suora.

Laaditaan merkkikaavio.

Vastaus: [[$\frac{1}{4}<x<1$]]

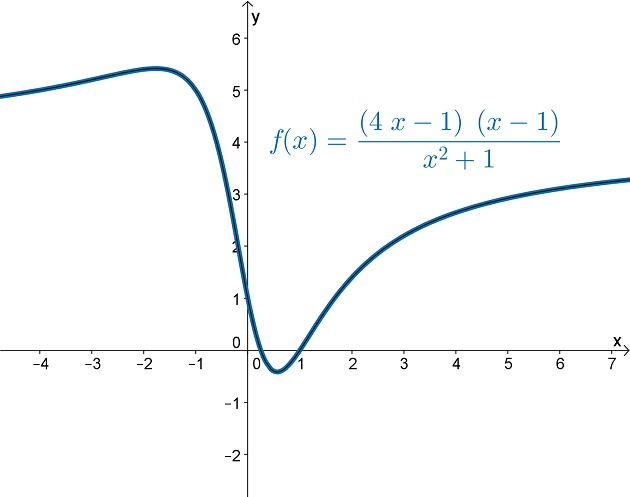
Tarkistetaan vastaus kuvaajasta:

Funktion kuvaaja todentaa saman kuin merkkikaavio, joten vastaus on oikea.

Esimerkki 2

Ratkaise murtoepäyhtälö [[$ \dfrac{x^2+2x-4}{x+1}<0 $]].

Ratkaisu:
[[$ \dfrac{x^2+2x-4}{x+1}<0 $]]

Määrittelyehto: Nimittäjän [[$x+1$]] pitää olla erisuuri kuin nolla eli [[$x+1 \neq 0$]], joten [[$x \neq -1$]].

Ratkaistaan osoittajan nollakohdat:

[[$ x^2+2x-4=0 $]], kun [[$ x=\sqrt{5}-1 $]] ja [[$ x=-\sqrt{5}-1 $]]

Osoittajan [[$x^2+2x-4$]] kuvaaja on ylöspäin aukeava paraabeli.

Nimittäjän [[$x+1$]] kuvaaja on nouseva suora.

Laaditaan merkkikaavio.

Huomioidaan määrittelyehto eli [[$x \neq -1$]].

Epäyhtälö toteutuu, kun [[$ x< -\sqrt{5}-1 $]] tai [[$ -1<x<\sqrt{5}-1 $]].

Vastaus: [[$ x< -\sqrt{5}-1 $]] tai [[$ -1<x<\sqrt{5}-1 $]].

Tarkistetaan vastaus kuvaajasta.

Funktion kuvaaja lähestyy asymptoottia [[$x=-1$]] eli nimittäjän nollakohtaa, mutta ei kosketa sitä. Kuvaaja on [[$x$]]-akselin alapuolella, kun [[$ x< -\sqrt{5}-1 $]] tai [[$ -1<x<\sqrt{5}-1 $]], joten vastaus on oikein.

Esimerkki 3

Ratkaise murtoepäyhtälö [[$ \dfrac{x^2-2x-3}{x^2-1}\geq0$]].

Ratkaisu:
[[$ \dfrac{x^2-2x-3}{x^2-1}\geq0$]]

Määrittelyehdot:

[[$ \begin{align}x^2-1& \neq 0& \parallel&+1\\x^2& \neq 1& \parallel& \sqrt{}\\x& \neq \pm1 \end{align} $]]

Ratkaistaan osoittajan nollakohdat.
[[$x^2-2x-3=0$]], kun [[$x=-1$]] ja [[$x=3$]].

Nyt on huomattava, että osoittajalla ja nimittäjällä on sama nollakohta [[$x=-1$]].

Osoittaja voidaan ilmoittaa tulomuodossa [[$(x+1)(x-3)$]] ja nimittäjä [[$(x+1)(x-1)$]], jolloin epäyhtälö saadaan muotoon
[[$$ \begin{align}\frac{(x+1)(x-3)}{(x+1)(x-1)}& \geq0& \text{supistetaan}\ x+1\ \text{pois}\\ \frac{x-3}{x-1}& \geq0 \end{align} $$]]

Nyt nimittäjän nollakohta on [[$x=1$]] eli määrittelyehto supistuu muotoon [[$x \neq 1$]].

Osoittajan [[$x-3$]] kuvaaja on nouseva suora.
Nimittäjän [[$x-1$]] kuvaaja on nouseva suora.

Laaditaan merkkikaavio.

Huomioidaan määrittelyehto [[$x \neq 1$]]. Epäyhtälö toteutuu, kun [[$x<1$]] tai [[$x\geq3$]].

Vastaus: [[$x<1$]] tai [[$x\geq3$]]

Tarkistetaan vastaus kuvaajasta.

Funktion kuvaaja lähestyy asymptoottia [[$x=1$]], mutta ei kosketa sitä. Kuvaaja on [[$x$]]-akselin yläpuolella, kun [[$x<1$]] tai [[$x>3$]], joten vastaus on oikein.