Ensimmäisen asteen funktiolla [[$ f(x)=ax+b $]]​ ([[$ a \neq0 $]]​) on yksi nollakohta.
Jos [[$ a>0 $]], kuvaaja on nouseva suora.
Jos [[$ a<0 $]]​, kuvaaja on laskeva suora.
Jos [[$ a=0 $]]​, funktio ei ole ensimmäisen asteen funktio, vaan vakiofunktio [[$ f(x)=b $]]​. Tällöin sillä ei ole nollakohtaa (ellei ole [[$b=0$]]) ja kuvaaja on vaakasuora suora.

Esimerkki 1

Funktion [[$ f(x)=3 $]]​ kuvaaja on vaakasuora suora.

Yllä oleva vakiofunktio saa kaikilla muuttujan [[$ x $]] arvoilla positiivisen arvon [[$ 3 $]]​.

Esimerkki 2

a) Millä muuttujan [[$ x $]] arvoilla funktion kuvaaja on [[$ x $]]-akselin
i) yläpuolella
ii) alapuolella?
b) Ilmoita kuviossa funktion merkin vaihtelu.
c) Laadi merkkikaavio.

Ratkaisu:
a) Funktion kuvaaja on [[$ x $]]-akselin yläpuolella, kun [[$ x > 2 $]]​ eli kuvion oranssilla osuudella.



Funktion kuvaaja on [[$ x $]]-akselin alapuolella, kun [[$ x<2 $]] eli kuvion vihreällä osuudella.



b) Funktion merkki on oranssilla alueella [[$ + $]] ja vihreällä alueella [[$ - $]].

c) Merkkikaavio:

Esimerkki 3

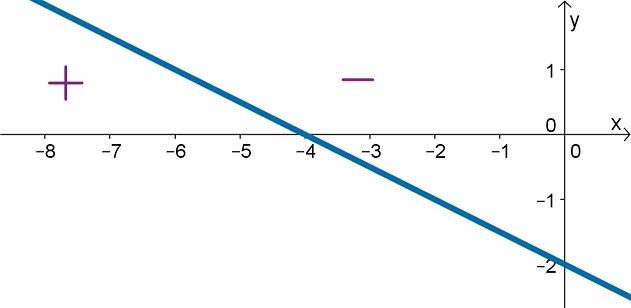
Laadi oheisen funktion merkkikaavio.

Ratkaisu:
Funktion kuvaaja on [[$ x $]]-akselin yläpuolella, kun [[$ x<-4 $]]. Vastaavasti kuvaaja on [[$ x $]]-akselin alapuolella, kun [[$ x>-4 $]]. Tällöin funktio saa positiivisia arvoja, kun [[$ x<-4 $]] ja negatiivisia arvoja, kun [[$ x>-4 $]].

Vastaus: Merkkikaavio: