5.4 Toisen asteen epäyhtälö

Määritelmä

Toisen asteen epäyhtälössä muuttujan korkein eksponentti on [[$2$]].

Epäyhtälö on esimerkiksi muotoa [[$ ax^2+bx+c<0 $]].

Toisen asteen epäyhtälön ratkaiseminen algebrallisesti

Epäyhtälö saatetaan muotoon

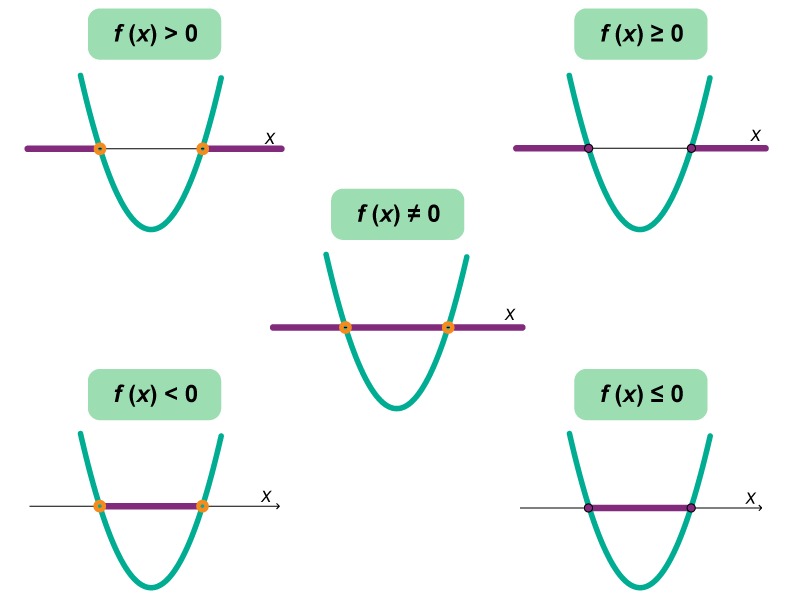
[[$ f(x) < 0 \qquad f(x) $]] on pienempi kuin nolla
​[[$ f(x) \leq 0 \qquad f(x) $]] on pienempi tai yhtä suuri kuin nolla
[[$ f(x) > 0 \qquad f(x) $]] on suurempi kuin nolla
[[$ f(x) \geq 0 \qquad f(x) $]] on suurempi tai yhtä suuri kuin nolla
[[$ f(x) \neq 0 \qquad f(x) $]] on erisuuri kuin nolla



Toisen asteen epäyhtälön ratkaiseminen algebrallisesti

  1. Siirretään kaikki termit epäyhtälömerkin vasemmalle puolelle, elleivät ne jo ole siellä. Oikealle puolelle jää pelkästään nolla.
  2. Sievennetään epäyhtälö niin pitkälle kuin mahdollista.
  3. Ratkaistaan funktion nollakohdat eli muuttujan [[$x$]] arvot, joilla [[$ f(x) = 0 $]]​.
  4. Katsotaan, onko epäyhtälössä toisen asteen termin kerroin [[$ a $]]​ positiivinen vai negatiivinen, eli aukeaako paraabeli ylöspäin vai alaspäin.
  5. Piirretään tyyppikuvaaja ja/tai tehdään merkkikaavio.
  6. Katsotaan merkkikaaviosta tai tyyppikuvaajasta, mitkä muuttujan [[$x$]] arvot toteuttavat epäyhtälön (tarkistetaan kuuluvatko nollakohdat ratkaisujoukkoon).
  7. Epäyhtälön vastaus voidaan tarkistaa sijoittamalla epäyhtälöön jokin kyseisellä välillä oleva muuttujan [[$x$]] arvo ja laskemalla, toteutuuko epäyhtälö.

Jos epäyhtälö on muotoa [[$ f(x)\neq g(x) $]], molemmilta puolilta vähennetään [[$ g(x) $]]. Epäyhtälö saadaan muotoon [[$ f(x)-g(x)\neq0 $]]. Tämä epäyhtälö ratkaistaan laskemalla polynomin [[$ (f(x)-g(x)) $]] nollakohdat. Epäyhtälö toteutuu tällöin kaikilla muilla muuttujan [[$ x $]] reaalilukuarvoilla paitsi polynomin nollakohdissa. Toinen vaihtoehto on ratkaista epäyhtälö kuten yhtälö, mutta yhtäsuuruusmerkin [[$=$]] tilalla käytetään erisuuruusmerkkiä [[$ \neq $]]​.

Epäyhtälön toteuttava alue

Alla olevissa kuvioissa epäyhtälön toteuttava alue on merkitty violetilla värillä. Funktion nollakohdat, jotka eivät kuulu ratkaisujoukkoon, on merkitty oranssilla.

Esimerkki 1

Ratkaise epäyhtälö [[$ -3x^2+x+2 >6x $]]​.

Ratkaisu:[[$$ \begin{align} -3x^2+x+2&>6x& ∥-6x\\ -3x^2+x-6x+2&>6x-6x &&\text{sievennetään}\\ -3x^2-5x+2&>0 \end{align} $$]]
Nyt epäyhtälö on muotoa [[$ f(x)>0 $]]​. Ratkaistaan funktion nollakohdat: [[$ -3x^2-5x+2=0 $]].
Nollakohdat ovat [[$ x=-2 $]] ja [[$ x=\frac{1}{3} $]]​​.

Koska polynomin [[$ -3x^2-5x+2 $]] toisen asteen termin kerroin [[$ a $]]​ on negatiivinen, funktion kuvaaja on alaspäin aukeava paraabeli.

Laaditaan merkkikaavio nollakohtien ja paraabelin aukeamissuunnan perusteella.


Toisen asteen epäyhtälössä merkkikaavio ei ole välttämätön, vaan vastaus voidaan lukea myös tyyppikuvaajasta.

Epäyhtälö [[$ -3x^2-5x+2>0 $]]​ toteutuu silloin, kun [[$ -2<x<\frac{1}{3} $]]​

Vastaus: [[$ -2<x<\frac{1}{3} $]]

Vastaus voidaan tarkistaa, kun alkuperäiseen epäyhtälöön sijoitetaan jokin muuttujan [[$x$]] arvo kultakin lukusuoran väliltä, esimerkiksi [[$ x=-3, x=-1 $]] ja​ [[$ x=1 $]]​.

[[$-3x^2 - 5x + 2$]]
[[$x = -3$]] [[$-3 \cdot (-3)^2 - 5 \cdot (-3) + 2 = -10$]] negatiivinen
[[$x = -1$]] [[$-3 \cdot (-1)^2 - 5 \cdot (-1) + 2 = 4$]] positiivinen
[[$x = 1$]] [[$-3 \cdot 1^2 - 5 \cdot 1 + 2 = -6$]] negatiivinen

Vastaus pitää paikkansa.

Esimerkit 2 ja 3

Esimerkki 2

Ratkaise epäyhtälö [[$ -3x+1\leq-x^2-x $]].

Ratkaisu:
[[$$ \begin{align} -3x+1&\leq-x^2-x& ∥&+x^2+x\\ x^2-2x+1&\leq0\end{align} $$]]​
Lasketaan nollakohdat eli ratkaistaan yhtälö [[$ x^2-2x+1=0 $]]. Ainoa nollakohta on pisteessä [[$ x=1 $]].

Polynomin [[$ x^2-2x+1 $]] kuvaaja on ylöspäin aukeava paraabeli.

Epäyhtälö [[$ -3x+1\leq-x^2-x $]] toteutuu ainoastaan kohdassa [[$ x=1 $]].

Vastaus: [[$ x=1 $]]

Tarkistetaan vastaus funktioiden kuvaajien avulla.


Suora ja paraabeli sivuavat toisiaan kohdassa [[$ x=1 $]] eikä suora ole millään muuttujan [[$ x $]] arvolla paraabelin alapuolella. Tällöin vain arvo [[$ x=1 $]] toteuttaa epäyhtälön [[$ -3x+1\leq-x^2-x $]].

Esimerkki 3

Ratkaise epäyhtälö [[$ x^2+8x-9\neq0 $]]​.

Ratkaisu:
Ratkaistaan funktion nollakohdat eli [[$ x^2+8x-9=0 $]].​
Nollakohdat ovat [[$ x=-9 $]]​ ja [[$ x=1 $]]​. Epäyhtälön vasemman puolen pitää olla erisuuri kuin nolla, joten ratkaisujoukkona ovat kaikki muut reaaliluvut kuin nollakohdat.

Vastaus: [[$ x\neq-9 $]]​ tai [[$ x\neq1 $]]​

Esimerkki 4

Ratkaise epäyhtälö [[$ 2x\leq3x^2 $]]​.

Ratkaisu:
[[$$\begin{align}2x&\leq3x^2&\parallel-3x^2\\-3x^2+2x&\leq0\end{align}$$]]
Ratkaistaan funktion [[$ f(x)=-3x^2+2x $]] nollakohdat.
Nollakohdat ovat [[$ x=0 $]]​ ja [[$ x=\frac{2}{3} $]]​.

Funktion kuvaaja on alaspäin aukeava paraabeli.


Vastaus: [[$ x\leq0 $]]​ tai [[$ x\geq\frac{2}{3} $]]​

Ratkaisutapa 2:

Toinen vaihtoehto ratkaista epäyhtälö on jakaa molemmat puolet muuttujalla [[$ x $]]​.
[[$$ 2x\leq3x^2\ \ \parallel:x $$]]​
[[$ x $]]​:llä kertomisessa ja jakamisessa tulee olla hyvin varovainen, koska ei tiedetä, onko [[$ x $]] positiivinen vai negatiivinen. Pitää myös huomioida, että nollalla ei saa jakaa, joten [[$ x $]] ei jaettaessa voi olla nolla eli [[$ x\neq0 $]]!

Jos epäyhtälö jaetaan muuttujalla [[$ x $]], pitää ratkaista erikseen tapaukset, joissa [[$ x $]] on positiivinen ja tapaukset, joissa [[$ x $]] on negatiivinen.

  • Jos [[$ x $]] on negatiivinen, epäyhtälömerkin suunta pitää kääntää.
  • Jos [[$ x $]] on positiivinen, merkin suunta ei käänny.
[[$ x=0 $]] saattaa myös kuulua vastausjoukkoon, joten pitää erikseen tutkia tapaus, toteuttaako [[$ x=0 $]] epäyhtälön.


Jos [[$ x>0 $]]:
[[$$ \begin{align}2x&\leq3x^2& \parallel:x\\2&\leq3x& \parallel:3\\\frac{2}{3}&\leq x\end{align}$$]]

Yhdistämällä molemmat ehdot [[$ x>0 $]]​ ja [[$ x\geq\frac{2}{3} $]] saadaan [[$ x\geq\frac{2}{3} $]].

Jos [[$ x<0 $]]:
[[$$ \begin{align}2x&\leq3x^2& \parallel:x&&\text{merkki kääntyy!}\\2&\geq3x& \parallel:3\\\frac{2}{3}&\geq x\end{align}$$]]

Yhdistämällä molemmat ehdot [[$ x<0 $]]​ ja [[$ x\leq\frac{2}{3} $]]​ saadaan [[$ x<0 $]].

Jos [[$ x=0 $]]:
[[$$\begin{align}2x&\leq3x^2\\2\cdot0&\leq3\cdot0^2\\0&\leq0&&\text{tosi}\end{align}$$]]

Siten piste [[$ x=0$]] kelpaa ratkaisuksi.

Yhdistetään kaikki vastaukset.

Vastaus: [[$ x\leq0 $]]​ tai [[$ x\geq\frac{2}{3} $]]​

Sovelma toisen asteen epäyhtälöstä

Alla olevalla sovelmalla voit tutkia toisen asteen epäyhtälön toteutumista, kun se on muotoa [[$ ax^2+bx+c<0 $]] tai [[$ ax^2+bx+c>0 $]]​.

Liu’uista voit muuttaa [[$ a $]]​:n, [[$ b $]]​:n ja [[$ c $]]​:n arvoja. Funktion kuvaaja näkyy punaisena, kun sen arvot ovat positiivisia ja sinisenä, kun arvot ovat negatiivisia. Klikkaamalla ruutua ”näytä nollakohdat”, saat funktion nollakohdat näkyviin. Ruuduista ”näytä vastaus” voit tarkistaa vastauksen.


Toisen asteen epäyhtälön ratkaiseminen graafisesti

Epäyhtälön voi ratkaista myös graafisesti, mikäli tehtävässä niin pyydetään.
Graafisella tarkastelulla voi myös tarkistaa algebrallisesti saadun vastauksen paikkansapitävyyden.

Toisen asteen epäyhtälön [[$ f(x)>g(x) $]]​ ratkaiseminen graafisesti

  1. Piirretään funktioiden [[$ f(x) $]] ja [[$ g(x) $]] kuvaajat samaan koordinaatistoon
  2. Jos kuvasta ei yksiselitteisesti selviä funktioiden [[$ f(x) $]] ja [[$ g(x) $]] kuvaajien leikkauspisteet, ne lasketaan. Merkitään [[$ f(x)=g(x) $]] ja ratkaistaan [[$ x $]]
  3. Katsotaan kuvasta, milloin [[$ f(x)>g(x) $]]​. Epäyhtälö toteutuu niillä muuttujan [[$ x $]] arvoilla, joilla [[$ f(x) $]]:n kuvaaja on [[$ g(x) $]]:n kuvaajan yläpuolella

Jos epäyhtälö on muotoa [[$ f(x) \geq g(x) $]], ratkaisuun otetaan mukaan myös funktioiden [[$ f(x) $]] ja [[$ g(x) $]] kuvaajien leikkauspisteiden [[$ x $]]-koordinaatit.

Jos epäyhtälö on muotoa [[$ f(x) \neq g(x) $]], se toteutuu kaikilla muilla muuttujan [[$ x $]] arvoilla paitsi funktioiden [[$ f(x) $]] ja [[$ g(x) $]] kuvaajien leikkauspisteissä.

Esimerkki 5

Ratkaise [[$ -3x^2+3>x^2+7x+1 $]]​.

Ratkaisu:

Kuvaajasta tarkastellaan, milloin [[$ -3x^2+3 $]] on suurempi kuin [[$ x^2+7x+1 $]] eli millä muuttujan [[$ x $]] arvoilla sininen paraabeli on ylempänä kuin vihreä paraabeli. Paraabelien leikkauskohtia ei näe tarkasti kuvaajasta, joten ne kannattaa laskea.

[[$ \begin{align}-3x^2+3&=x^2+7x+1 \ & ∥-x^2-7x-1\\-x^2-7x+2&=0\end{align} $]]

Leikkauskohdat ovat [[$ x=-2 $]] ja [[$ x=\frac{1}{4} $]].
Epäyhtälö toteutuu näiden pisteiden välissä, koska silloin sininen paraabeli on vihreän paraabelin yläpuolella.

Vastaus: [[$ -2<x<\frac{1}{4} $]]​

Esimerkki 6

Ratkaise epäyhtälö [[$ -2x-1>x^2-2x+4 $]]​ graafisesti ja tarkista vastaus algebrallisesti.

Ratkaisu:

Suora ja paraabeli eivät leikkaa missään pisteessä eli suora [[$ -2x-1 $]]​ ei ole paraabelin [[$ x^2-2x+4 $]] yläpuolella millään muuttujan [[$ x $]] arvolla.

Vastaus: Epäyhtälöllä ei ole ratkaisua. (Vastauksen voi ilmoittaa myös muodossa [[$ R_{j}= $]] {[[$ \phi $]]​})

Tarkistus: [[$$ \begin{align} -2x-1&>x^2-2x+4 \ & ∥-x^2+2x-4\\ -2x-1-x^2+2x-4&>0 \ & \text{sievennetään}\\ -x^2-5&>0 \end{align} $$]]
Lasketaan funktion [[$ f(x)=-x^2-5 $]] ​nollakohdat.
[[$ f(x)=-x^2-5 $]] ei ole nolla millään muuttujan [[$ x $]] arvolla eli sillä ei ole nollakohtia.

Funktion [[$ f(x)=-x^2-5 $]] kuvaaja on alaspäin aukeava paraabeli ja koska sillä ei ole nollakohtia, [[$ -x^2-5<0 $]] kaikilla muuttujan [[$ x $]] arvoilla.

Tällöin epäyhtälöllä ei ole ratkaisua.

Esimerkki 7

Ratkaise epäyhtälö [[$ x^2-x+3>\text{0,3}x^2+1 $]]​ graafisesti ja tarkista vastaus algebrallisesti.

Ratkaisu:

Vihreä paraabeli [[$ y=x^2-x+3 $]] ​on aina sinisen paraabelin [[$ y=\text{0,3}x^2+1 $]]​ yläpuolella, joten epäyhtälö toteutuu kaikilla muuttujan [[$ x $]] arvoilla.

Vastaus: Epäyhtälö on kaikilla muuttujan [[$ x $]] arvoilla tosi. (Vastaus voidaan merkitä myös muodossa [[$ R_{j}=\mathbb{R} $]]​)

Tarkistus: [[$$ \begin{align} x^2-x+3&>\text{0,3}x^2+1 \ & ∥-\text{0,3}x^2-1\\ x^2-x+3-\text{0,3}x^2-1&>0 \ & \text{sievennetään}\\ \text{0,7}x^2-x+4&>0 \end{align} $$]]

Lasketaan funktion [[$ h(x)=\text{0,7}x^2-x+4 $]] ​nollakohdat.
Funktiolla ei ole nollakohtia. Sen kuvaaja on ylöspäin aukeava paraabeli.

Tällöin epäyhtälö toteutuu kaikilla muuttujan [[$ x $]] arvoilla.

Toisen asteen kaksoisepäyhtälö

Toisen tai korkeamman asteen kaksoisepäyhtälö ratkaistaan vastaavasti kuten ensimmäisen asteen kaksoisepäyhtälö. Epäyhtälö [[$ f(x)<g(x)<h(x) $]] jaetaan kahdeksi erilliseksi epäyhtälöksi [[$ f(x)<g(x) $]] ja [[$ g(x)<h(x) $]].

Tutkitaan merkkikaavion avulla, millä muuttujan [[$x$]] arvoilla molemmat epäyhtälöt toteutuvat.

Esimerkki 8

Ratkaise [[$ -x-2<-x^2\leq-3x $]]​.

Ratkaisu:
Jaetaan kaksoisepäyhtälö kahdeksi epäyhtälöksi eli [[$ -x-2<-x^2 $]]​ ja [[$ -x^2<-3x $]]​.

Ratkaistaan ensimmäinen epäyhtälö.
[[$ \begin{align}-x-2&<-x^2 \ & ∥+x^2\\x^2-x-2&<0 \end{align} $]]

Ratkaistaan funktion [[$ f(x)=x^2-x-2 $]]​ nollakohdat.

[[$ x^2-x-2=0 $]], kun [[$ x=-1 $]] tai [[$ x=2 $]].​​

Koska funktion toisen asteen termin kerroin [[$ 1 $]]​ on positiivinen, kuvaaja on ylöspäin aukeava paraabeli.


Ensimmäisen epäyhtälön ratkaisu on [[$ -1<x<2 $]].

Ratkaistaan toinen epäyhtälö.
[[$ \begin{align} -x^2&\leq-3x \ & ∥+3x\\ -x^2+3x&\leq0 \end{align} $]]

Ratkaistaan funktion [[$ g(x)=-x^2+3x $]] ​nollakohdat.

[[$ -x^2+3x=0 $]], kun [[$ x=0 $]] tai [[$ x=3 $]].​​

Koska funktion toisen asteen termin kerroin [[$ -1 $]]​ on negatiivinen, kuvaaja on alaspäin aukeava paraabeli.


Toisen epäyhtälön ratkaisu on [[$ x\leq0 $]] tai [[$ x\geq3 $]].

Laaditaan merkkikaavio, johon merkitään kaikki nollakohdat suuruusjärjestyksessä. Merkkikaavioon merkitään ne välit, joilla edellä tarkastellut epäyhtälöt toteutuvat.


Molemmat epäyhtälöt toteutuvat, kun [[$ -1<x\leq 0 $]].

Vastaus: [[$ -1<x\leq 0 $]]

Kuvaajasta voidaan tarkistaa, pitääkö vastaus paikkansa.


Epäyhtälöissä esiintyneet funktiot [[$ f(x) $]] ja [[$ g(x) $]] saavat negatiivisia arvoja, kun [[$ -1<x<0 $]]​ eli vastaus on oikea.