Ratkaise epäyhtälö [[$ x^2-x+3>\text{0,3}x^2+1 $]]​ graafisesti ja tarkista vastaus algebrallisesti.

Ratkaisu:

Vihreä paraabeli [[$ y=x^2-x+3 $]] ​on aina sinisen paraabelin [[$ y=\text{0,3}x^2+1 $]]​ yläpuolella, joten epäyhtälö toteutuu kaikilla muuttujan [[$ x $]] arvoilla.

Vastaus: Epäyhtälö on kaikilla muuttujan [[$ x $]] arvoilla tosi. (Vastaus voidaan merkitä myös muodossa [[$ R_{j}=\mathbb{R} $]]​)

Tarkistus: [[$$ \begin{align} x^2-x+3&>\text{0,3}x^2+1 \ & ∥-\text{0,3}x^2-1\\ x^2-x+3-\text{0,3}x^2-1&>0 \ & \text{sievennetään}\\ \text{0,7}x^2-x+4&>0 \end{align} $$]]

Lasketaan funktion [[$ h(x)=\text{0,7}x^2-x+4 $]] ​nollakohdat.
Funktiolla ei ole nollakohtia. Sen kuvaaja on ylöspäin aukeava paraabeli.

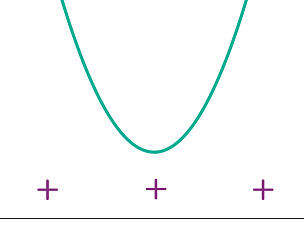Tällöin epäyhtälö toteutuu kaikilla muuttujan [[$ x $]] arvoilla.