Ratkaise murtoepäyhtälö [[$\dfrac{(4x-1)(x-1)}{x^2+1}<0$]].

Ratkaisu:
Määrittelyehto: Nimittäjä [[$x^2+1$]] on aina [[$>0$]], joten määrittelyjoukko on [[$\mathbb{R}$]]. Koska nimittäjä on aina positiivinen, epäyhtälön merkki riippuu vain osoittajasta.

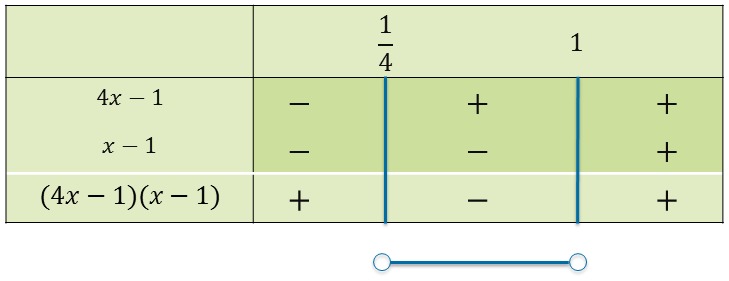
Tutkitaan binomien [[$4x-1$]] ja [[$x-1$]] merkkiä.
[[$$ \begin{align}4x-1&=0& \parallel &+1\\4x&=1& \parallel &:4\\x&=\frac{1}{4} \end{align} $$]]
[[$$ \begin{align}x-1&=0& \parallel +1\\x&=1 \end{align} $$]]

• Binomin [[$4x-1$]] kuvaaja on nouseva suora.

  ---

• Binomin [[$x-1$]] kuvaaja on nouseva suora.

  ---

Laaditaan merkkikaavio.

Vastaus: [[$\frac{1}{4}<x<1$]]

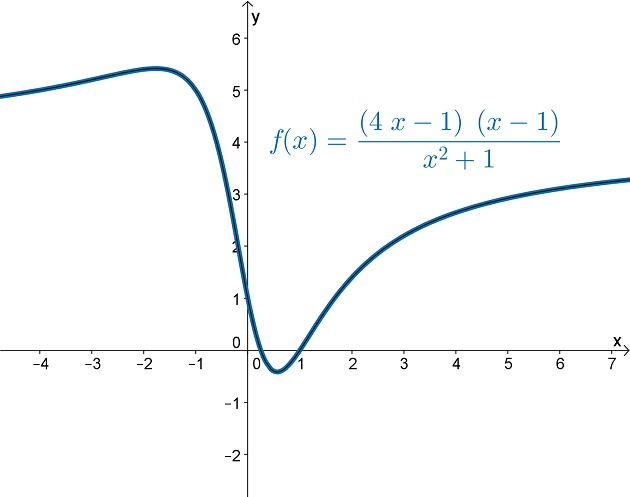
Tarkistetaan vastaus kuvaajasta:

Funktion kuvaaja todentaa saman kuin merkkikaavio, joten vastaus on oikea.