Pythagoraan lause
Teoria T1 Suorakulmainen kolmio
Suorakulmaisella kolmiolla on omat nimitykset kolmion sivuille:
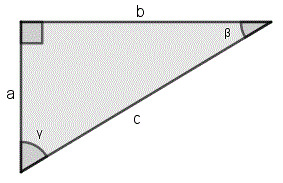
Suorakulmaisen kolmion pinta-alan voit laskea kaavalla
[[$ A=\frac{kanta \cdot korkeus}{2} = \frac{kateetti \cdot kateetti}{2}=\frac{a\cdot b}{2} $]]
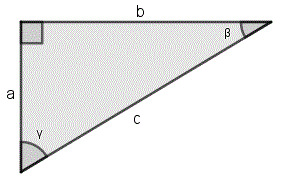
- sivut a ja b ovat kateetteja
- sivu c on hypotenuusa
Suorakulmaisen kolmion pinta-alan voit laskea kaavalla
[[$ A=\frac{kanta \cdot korkeus}{2} = \frac{kateetti \cdot kateetti}{2}=\frac{a\cdot b}{2} $]]

Peda.net tehtävä P1 Suorakulmainen kolmio
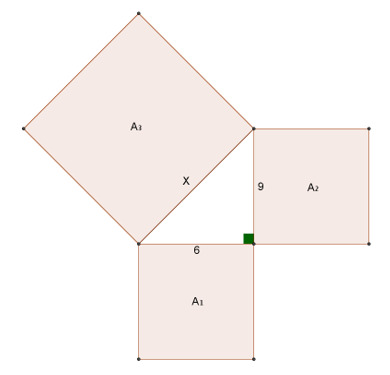
Kuva 1. Pythagolaan lause
Peda.net tehtävä P2 Pythagoraan lause
Video
Teoria T2 Pythagoraan lause
Pythagoraan lause:
Esimerkki: Suorakulmaisen kolmion kateettien pituudet ovat 5 ja 8. Laske hypotenuusan pituus x.
Ratkaisu: Merkataan Pythagoraan lauseen mukainen yhtälö kateetin neliö + kateetin neliö = hypotenuusan neliö
[[$ 5^2 + 8^2 = x^2 $]] eli
[[$ 25+64=x^2 $]]
[[$ 100 = x^2 $]], josta päättelmällä tai neliöjuuren avulla saadaan ratkaisuksi
[[$ 10 = x $]]
Vastaus: Hypotenuusan pituus on 10.
- kateetin neliöiden summa on hypotenuusan neliö eli
- kateetin neliö + kateetin neliö = hypotenuusan neliö
Matemaattisena kaavana: [[$ 𝒂^𝟐+𝒃^𝟐=𝒄^𝟐 $]]

Esimerkki: Suorakulmaisen kolmion kateettien pituudet ovat 5 ja 8. Laske hypotenuusan pituus x.
Ratkaisu: Merkataan Pythagoraan lauseen mukainen yhtälö kateetin neliö + kateetin neliö = hypotenuusan neliö
[[$ 5^2 + 8^2 = x^2 $]] eli
[[$ 25+64=x^2 $]]
[[$ 100 = x^2 $]], josta päättelmällä tai neliöjuuren avulla saadaan ratkaisuksi
[[$ 10 = x $]]
Vastaus: Hypotenuusan pituus on 10.
Peda.net tehtävä P3 Laskuja Pythagoraan lauseesta
Kuva 2
Oppimisen tavoitteet
- Syvennät taitoasi ratkaista 2. asteen yhtälöitä.
- Opit selittämään Pythagoraan lauseen pinta-alojen avulla.
- Opit hyödyntämään Pythagoraan lausetta geometrisissä ongelmissa
Arvosanan 8 osaaminen päättöarvioinnissa:
" Oppilas osaa käyttää Pythagoraan lausetta ja trigonometriaa suorakulmaisen kolmion osien ratkaisemiseen"