4.5 Logaritmi

4.5 Logaritmi

Tässä luvussa tarkastelemme logaritmifunktiota, joka on käänteinen toiminto eksponenttifunktiolle.

Tutkimus
Laske ensin laskimella eksponenttifunktion [[$10^x$]] arvoja, kun [[$x$]] saa kokonaislukuarvoja [[$-2,...,5$]]
Kirjaa tulokset.

Laske sen jälkeen laskimen log-näppäimellä lausekkeen [[$\log a$]] arvoja. Sijoita luvun [[$a$]] paikalle äsken saamasi tulokset. Mitä huomaat?

Katso tästä Tutkimuksen tulokset.

Etsi kuvaajan avulla seuraavien eksponenttilausekkeiden ja logaritmien arvot

Kirjaudu sisään lähettääksesi tämän lomakkeen

Alla olevassa sovelmassa on funktion [[$y= 2^x$]] kuvaaja. Kuvaajalta nähdään arvot [[$2^4 = 16$]] sekä [[$2^5 = 32$]]. Näin yhtälön [[$2^x = 32$]] ratkaisu on [[$x=5$]]. Lukua 5 kutsutaan luvun 32 2-kantaiseksi logaritmiksi. Luvun 16 2-kantainen logaritmi on taas 4. Se merkitään [[$\log_2 16 = 4$]].



Etsi kuvaajan avulla seuraavien eksponenttilausekkeiden ja logaritmien arvot. Anna vastaukset kahden desimaalin tarkkuudella (kokonaisluvut ilman pilkkua). Zoomaa ikkunaa tarvittaessa, jotta saat oikean lukuarvon näkyviin.

a) [[$2^7=$]]
b) [[$\log_2 64=$]]
c) [[$2^{2,6} = $]]
d) [[$\log_2 \text{46,4} =$]]

Kirjaudu sisään lähettääksesi tämän lomakkeen

Logaritmin määritelmä

Logaritmi merkitsee eksponenttiyhtälön ratkaisua

[[$x = \log_a b \Leftrightarrow a^x = b , \quad a > 0 , a \neq 1$]]

Logaritmin merkinnässä luku [[$a$]] on kantaluku ja luku [[$b$]] on numerus.


Funktion [[$2^x$]] kuvaaja saa kaikki positiiviset arvot. Funktion arvo kasvaa aina kun [[$x$]] kasvaa. Näin logaritmi on määritelty aina, kun [[$b > 0 $]] ja sen arvona voi olla mikä hyvänsä reaaliluku.

Logaritmifunktion kuvaajat


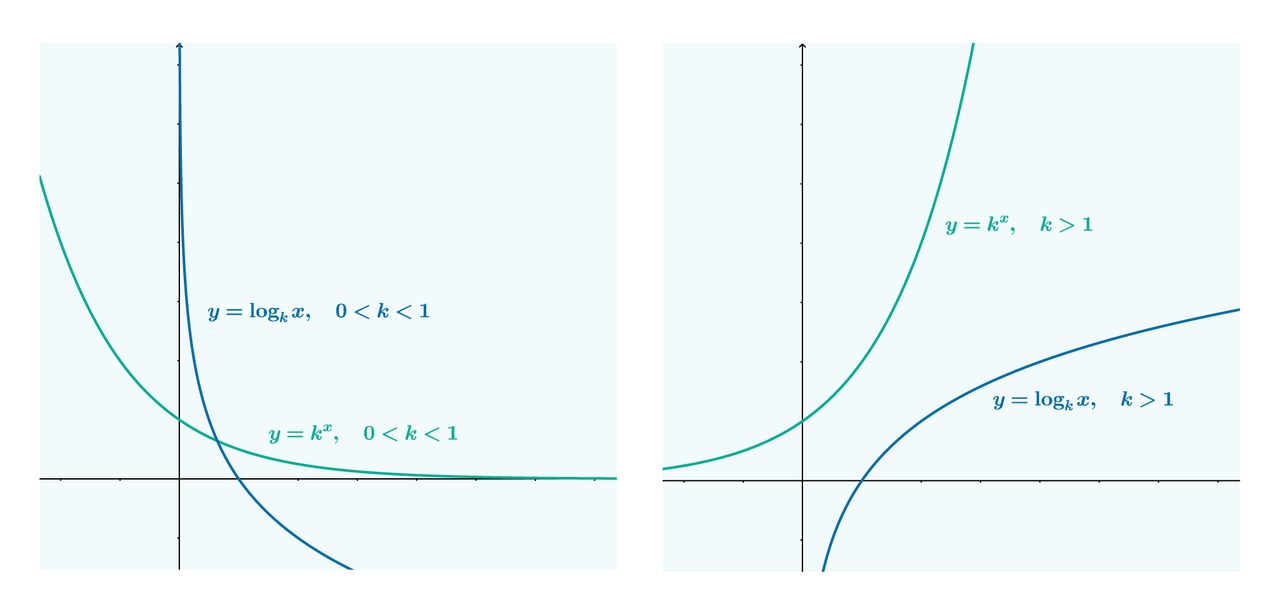
Logaritmifunktion määrittelyjoukko ja arvojoukko

[[$$ \begin{align} f(x) &= \log_a b \\ \mathbf{M}_f &= \mathbf{R}_+ \\ \mathbf{A}_f &= \textrm{R} \end{align} $$]]


Esimerkki 1

a) Merkitse luku [[$x$]] logaritmina, kun [[$5^x = 37$]]
b) Ratkaise luku [[$y$]], kun [[$\log_3 y = 2$]].

Ratkaisu:
a) Logaritmin määritelmän mukaan [[$a^x = b \Leftrightarrow x= \log_a b$]], joten [[$x = \log_5 37$]].

b) Logaritmin määritelmässä kantalukuna [[$a$]] on luku [[$3$]] ja logaritmin arvon [[$x$]] paikalla luku 2. Siten [[$y = 3^2 = 9 $]].

Logaritmijärjestelmät

Ensimmäisessä tutkimuksessa käytettiin kantalukua 10. Tavanomaisesti laskimesta löytyy kaksi logarimia. Näppäin log merkitsee logaritmia, jonka kantaluku on 10 sekä näppäin ln luonnollista logaritmia, jota ei käsitellä tässä kurssissa.

Briggsin logaritmi

Logaritmia, jonka kantaluku on kymmenen, kutsutaan Briggsin logaritmiksi ja merkitään [[$\log_{10} b = \lg b$]].

10-kantaisen logaritmin määritelmä

[[$$10^x = b \Leftrightarrow x = \lg b, \quad (b > 0 ) $$]]

Esimerkki 2

Ratkaise yhtälöt a) [[$10^x =243 \quad $]] b) [[$3\cdot 100^x =60$]]

Ratkaisu:
a) Logaritmin määritelmän mukaan [[$10^x = 243 \Leftrightarrow x = \lg 243 = \text{2,385}... \approx \text{2,39} $]]

b) Ratkaistaan ensin luvun 10 potenssi.
[[$ \begin{align} 3 \cdot 100^x &=60 &&| : 3 \\ 100^x&=20 &&| 100 = 10^2 \\ (10^2)^x &= 20 &&| (a^b)^c = a^{bc} \\ 10^{2x} &= 20 &&\\ 2x &= \lg 20 &&|:2 \\ x&=\frac{\lg 20 }{2} = \text{0,6505}... \approx \text{0,65}&& \end{align}$]]

Muut kantaluvut

Muut kantaluvut

Kun eksonenttiyhtälön kantaluku on muu kuin 10, ratkaisu saadaan käyttämällä kaavaa [[$\log_a b = \dfrac{\log_k b}{\log_k a}$]]. Tämä kaava perustellaan pitkän matematiikan kurssilla 8. Sillä saadaan laskettua logaritmin likiarvoja, kun valitaan kantaluvuksi [[$k$]] luku 10.

*Logaritmiin perustuvia mitta-asteikoita

Jotkin luonnonilmiöihin ja fysiikkaan liittyvät mitta-asteikot perustuvat logaritmiseen asteikkoon. Tällaisia ovat mm. liuoksen happamuutta kuvaava pH-asteikko sekä maanjäristyksien voimakkuuksien mittaus Richterin asteikkoon perustuvalla asteikolla. Lisätietoa näistä asteikosta löytyy alaluvusta 4.5.1.

Esimerkki 3

Ratkaise yhtälöt a) [[$6^x = 245\quad $]] b) [[$5^x = - 25$]]

Ratkaisu:
a)
[[$\begin{align}6^x&=245 &&|\text{ ratkaisu 6-kantaisena logaritmina} \\ x&= \log _6 245 &&|\text{ lasketaan likarvo käyttämällä muunnoskaavaa} \\ x &= \frac{\lg 245}{\lg 6} = \text{3,07}... \approx \text{3,1}&&\end{align}$]]

b) Eksponenttifunktio [[$5^x$]] saa vain positiivisia arvoja, eikä sen arvo voi koskaan olla yhtä suuri kuin –25. Siksi eksponenttiyhtälöllä ei ole ratkaisua. (Sama voidaan huomata myös ratkaisemalla [[$x=\log_5(-25)$]], jolloin negatiivisen luvun logaritmi ei ole määritelty.)

Esimerkki 4

Bakteerit lisääntyvät niin, että yksi bakteeri jakautuu kahdeksi uudeksi bakteeriksi vuorokauden kuluessa. Oletetaan, että alussa on yksi bakteeri. Kuinka monen vuorokauden kuluttua bakteereja on miljoona kappaletta?

Ratkaisu:
Bakteereja on yhden vuorokauden kuluttua 1 [[$\cdot$]] 2 = 2 kpl. Kahden vuorokauden kuluttua niitä on 1 [[$ \cdot$]] 2 [[$\cdot$]] 2 = 4 kpl, kolmen vuorokauden kuluttua 2 [[$\cdot$]] 2 [[$\cdot$]] 2 = 23 =8 kpl. Näin bakteerien määrä x vuorokauden kuluttua on 2x.

Muodostetaan yhtälö 2x = 1 000 000 ja ratkaistaan se logaritmin avulla.

[[$\begin{eqnarray} 2^x =& 1000000&& |\text{merkitään ratkaisu logaritmina} \\ x=&\log_2{1 000 000}&&|\log_a b = \frac{\log_k b}{\log_k a} \\x=&\frac{\lg 1 000 000}{\lg 2}&& \\ x = & \text{19,92}... \approx 20 && \end{eqnarray}$]]

Vastaus: Miljoonan raja on ylittynyt 20 vuoden kuluttua.

(Tehtävän ratkaisu voidaan tarkistaa laskemalla logaitmin arvo [[$ 2^{20} = 1 048 576 $]].)