4.4 Eksponentin ratkaiseminen
4.4 Eksponentin ratkaiseminen
Edellisessä kohdassa ratkaistiin juuren avulla eksponenttilausekkeesta [[$x^n$]] tuntematon [[$x$]], joka oli kantalukuna. Seuraavassa tutkitaan yhtälöä [[$a^x = b$]], jossa tuntematon on eksponentissa.
Funktiota [[$ f(x)=a^x$]], missä [[$a\in \mathbf{R}, a>0, a\neq 1$]] kutsutaan eksponenttifunktioksi. Toistaiseksi tunnemme eksponentin määritelmän, kun [[$x$]] on kokonaisluku, mutta funktio on määritelty kaikilla eksponentin [[$x \in \mathbf{R}$]] arvoilla.
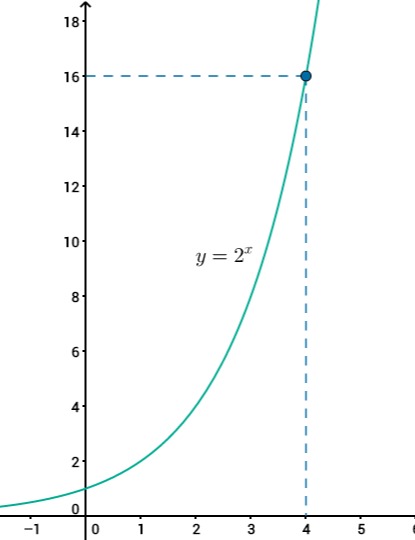
Tutkitaan esimerkkinä yhtälöä [[$2^x = 16$]].
Koska [[$16 = 4 \cdot 4 = 2\cdot 2\cdot 2\cdot 2= 2^4$]], luku [[$x=4$]] kelpaa yhtälön ratkaisuksi.
Tuntematon eksponentti saadaan siis ratkaistua, jos yhtälön molemmat puolet voidaan kirjoittaa saman kantaluvun potensseina.
[[$$ \begin{align} 2^x &=16 \\ 2^x &= 2^4 \\x &= 4 \end{align}$$]]
Edellä voidaan päätellä, että [[$x=4$]] on yhtälön ainoa ratkaisu, koska lausekkeen [[$4^x$]] arvo kasvaa eksponentin [[$x$]] kasvaessa ja pienenee vastaavasti eksponentin pienentyessä.
Eksponentin ratkaiseminen
Yhtälö [[$$a^x=b$$]]
voidaan ratkaista kirjoittamalla yhtälön molemmat puolet saman kantaluvun potenssina.
[[$$ \begin{eqnarray} & a^x&=b \quad &|b=a^n \\ \Leftrightarrow & a^x&=a^n & \\ \Leftrightarrow & x&=n& \end{eqnarray} $$]]
Esimerkki 1
Ratkaise yhtälöt [[$\qquad $]] a) [[$5^x=125 \qquad $]] b) [[$2^{3-2x}=2^{5-x}$]]
Ratkaisu:
a)
[[$\begin{align}& &5^x&=125 &&|125 = 5\cdot 5 \cdot 5 \\ &\Leftrightarrow \quad & 5^x &= 5^3 && \text{|kantaluvut samat, verrataan eksponentteja } \\ &\Leftrightarrow \quad &x&=3&{} &&\end{align}$]]
b)
[[$\begin{align} & &2^{3-2x}&=2^{5-x} && |\text{kantaluvut ovat samat} \\ &\Leftrightarrow \quad & 3-2x&=5-x &&| \text{ensimmäisen asteen yhtälö, tuntemattomat vasemmalle}\\ &\Leftrightarrow \quad &-2x + x & = 5-3 &&\\ &\Leftrightarrow \quad & -x&=2 &&| :(-1) \\ &\Leftrightarrow \quad &x &=-2 &&\end{align}$]]
Esimerkki 2
Ratkaise yhtälöt [[$\qquad$]]a) [[$ 7^x = \frac{1}{7} \qquad$]] b) [[$ 4^x = 2^{x+4} \qquad$]] c) [[$3 \cdot 2^x \cdot 2^x \cdot 2^x = 192 \qquad$]]
Ratkaisu:a)
[[$\begin{align} & &7^x &=\frac{1}{7} \qquad |\,\frac{1}{a}=a^{-1}\\ &\Leftrightarrow &7^x &= 7^{-1} \\ &\Leftrightarrow &x&= -1\end{align}$]]
b)
[[$\begin{align} & &4^x &= 2^{x+4}& &|\,4 = 2^2\\ &\Leftrightarrow \quad &(2^2)^x &=2^{x+4}& &|\,(a^b)^c=a^{bc} \\ &\Leftrightarrow \quad &2^{2x}&=2^{x+4}& &|\text{ sama kantaluku }\\ &\Leftrightarrow \quad &2x &= x+4&&\\ &\Leftrightarrow \quad &x&=4 & &\end{align} $]]
c)
[[$\begin{align} & &3 \cdot 2^x \cdot 2^x \cdot 2^x &= 192&& |:3 \quad \text{ Huomaa laskujärjestys} \\ &\Leftrightarrow &2^x \cdot 2^x \cdot 2^x &= 64 & &|\, a^n \cdot a^m = a^{m+n} \\ &\Leftrightarrow &2^{x+x+x} &= 8 \cdot 8 &&| \, 8 = 2^3 \\ &\Leftrightarrow &2^{3x} &=2^3 \cdot 2^3 &&| \, a^n \cdot a^m = a^{m+n} \\ &\Leftrightarrow &2^{3x}&=2^6 &&\\&\Leftrightarrow&3x&=6 &&|:3 \\ &\Leftrightarrow &x&=2&&\end{align} $]]