Logaritmin määritelmä
Logaritmi merkitsee eksponenttiyhtälön ratkaisua
[[$x = \log_a b \Leftrightarrow a^x = b , \quad a > 0 , a \neq 1$]]Logaritmin merkinnässä luku [[$a$]] on kantaluku ja luku [[$b$]] on numerus.
Funktion [[$2^x$]] kuvaaja saa kaikki positiiviset arvot. Funktion arvo kasvaa aina kun [[$x$]] kasvaa. Näin logaritmi on määritelty aina, kun [[$b > 0 $]] ja sen arvona voi olla mikä hyvänsä reaaliluku.
Logaritmifunktion kuvaajat
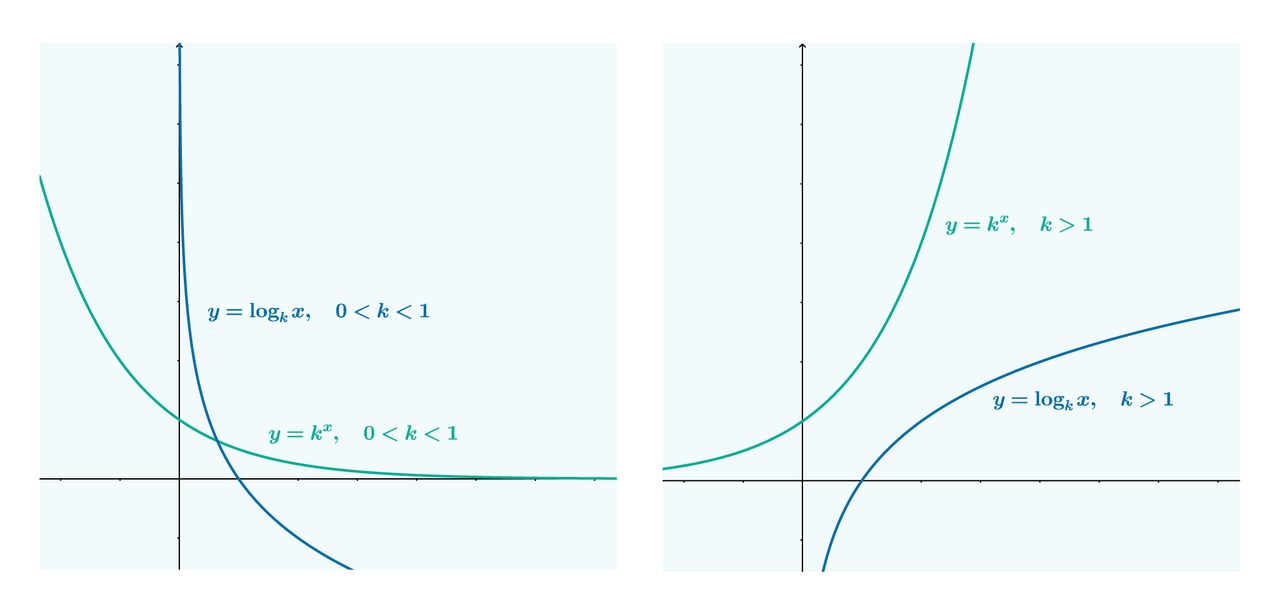
Logaritmifunktion määrittelyjoukko ja arvojoukko
[[$$ \begin{align} f(x) &= \log_a b \\ \mathbf{M}_f &= \mathbf{R}_+ \\ \mathbf{A}_f &= \textrm{R} \end{align} $$]]
Esimerkki 1
a) Merkitse luku [[$x$]] logaritmina, kun [[$5^x = 37$]]
b) Ratkaise luku [[$y$]], kun [[$\log_3 y = 2$]].
Ratkaisu:
a) Logaritmin määritelmän mukaan [[$a^x = b \Leftrightarrow x= \log_a b$]], joten [[$x = \log_5 37$]].
b) Logaritmin määritelmässä kantalukuna [[$a$]] on luku [[$3$]] ja logaritmin arvon [[$x$]] paikalla luku 2. Siten [[$y = 3^2 = 9 $]].