1. Trigonometriaa
Radiaani
Yksikköympyrä
Trigonometriset funktio, kulman sini ja kosini (+tangetti) määritellään yksikköympyrällä, jonka keskipiste on origo ja säde on 1.
%5E2%2B%5Cleft(y-0%5Cright)%5E2%3D1%5E2%5Cright))
Koordinaatistossa tämän ympyrän yhtälö keskipistemuodossa on
Kulman kärki on origossa ja kulman alkukylki on aina x-akselin positiivinen osa.
Jokaisella kulmalla α on kehäpiste P eli piste, jossa kulman loppukylki leikkaa ympyrän kehän.

%5C%20keh%C3%A4piste%5C%20on%5C%20%5Cleft(0%7B%2C%7D%5C%201%5Cright)) Sama ympyrän kehäpiste voi olla usealla eri kulmalla
Sama ympyrän kehäpiste voi olla usealla eri kulmalla
%5C%20vastaavat%5C%20kulmat%5C%20%5Cpi%7B%2C%7D%5C%20%5Cpi%2B2%5Cpi%3D3%5Cpi%7B%2C%7D%5C%20%5Cpi%2B2%5Ccdot2%5Cpi%3D5%5Cpi%5C%20jne)

Kirjan tehtäviä 101 - 106
Kotitehtävät: 108, 109 ja 112

Esimerkiksi
Tarkastellaan kehäpistettä (-1, 0)
sitä vastaa kulma π, mutta jos tähän kulmaan lisätään tai vähennetään täysi kierros 2π tai täysiä kierroksia
päädytään samaan kehäpisteeseen
Kirjan tehtäviä 101 - 106
Kotitehtävät: 108, 109 ja 112
Sinin ja kosinin määritelmä
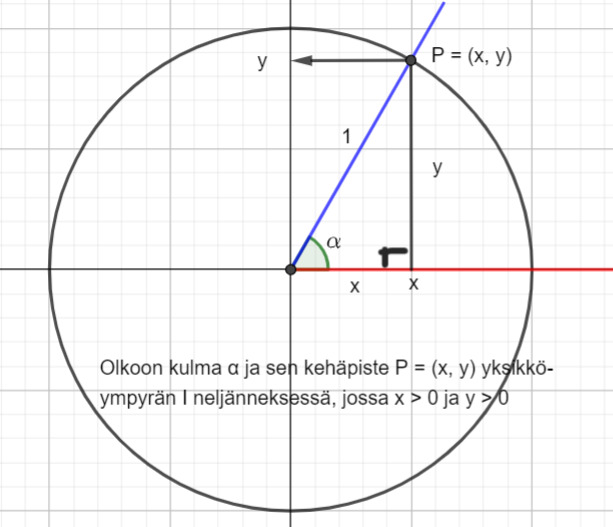
Kulman α sini ja kosini voidaan määritellä kuvan suorakulmaisen kolmion avulla, jossa kateetit ovat x ja y sekä hypotenuusa 1 (ympyrän säde).
eli kulman kosini on kehäpisteen x-koordinaatti
Tämä on voimassa kaikille kulmille α
Nyt nähdään yksikköympyrältä helposti, että kulman π kehäpiste (-1, 0).
Tämän perusteella sinπ =0 ja cosπ = -1 (nähdään myös laskimella tai taulukkokirjasta)
Sinin ja kosinin etumerkit eri neljänneksissä:

Kotitehtävät: 123, 125 ja 127
Sinin ja kosinin perusominaisuuksia
1. Arvojoukko
eli sinin ja kosinin arvojoukko on [-1, 1]
koska yksikköympyrällä kehäpisteen x ja y-koordinaatti on suurimmillaan 1 ja pienimmillään -1
2. Jaksollisuus
Jos kulmaan α lisätään tai vähennetään täysiä kierroksia niin päädytään samaan kehäpisteeseen.
Sanotaan, että sinin ja kosinin jaksona on 2π (ovat 2π jaksollisia)
3. Trigonometrian perusyhtälö
Kuvan suorakulmaiselle kolmiolle on voimassa Pythagoraan lause
Tämä on Pythagoraan lause yksikköympyrällä (ympyrän jokainen kehäpiste toteuttaa yhtälön)
Määritä kulman α kehäpiste, kun
a)
Nyt saadaan kehäpisteelle tarkka arvo, jolloin käytetään taulukkoa apuna.
Taulukoikossa on tarkat arvot kulmille väliltä 0 - 2π. Jos kulma ei ole tällä välillä niin silloin voidaan käyttää sinin ja kosinin jaksollisuutta eli lisätään tai vähennetään tähän kulmaan 2π tai sen monikertoja.
b)
Jos kulma on yli 2π niin silloin voidaan vähentää 2π tai sen monikertoja
Huom!
Voidaan ajatella myös seuraavasti:
Kotitehtävät: 137, 140 ja 142
Muita ominaisuuksia

Peilataan kulman α kehäpiste P = (x, y) y-akselin suhteen. Saadaan uusi kehäpiste, jossa y-koord säilyy samana ja x-koord muuttuu vastakkaismerkkiseksi eli uusi kehäpiste P = (-x, y), joka on kulman π - α kehäpiste. Tämän perusteella saadaan
eli kulman ja sen suplementtikulman sinit ovat yhtäsuuret.
Jos α-kulman kehäpiste P = (x, y) peilataan x-akselin suhteen niin kehäpisteen x-koord säilyy samana mutta y-koord muuttuu vastakkaismerkkiseksi eli kulman α vastakulman, -α:n kehäpiste P = (x, -y)
Trigonometrian perusyhtälö
Tässä kulman α kehäpiste P = (x, y) = (cosα, sinα) eli kyseessä on Pythagoraan lause yksikköympyrällä.
Trig perusyhtälöä joudutaan käyttämään, jos tiedetään sinα ja joudutaan määrittämään cosα (tai päinvastoin)
Esimerkki
Mietitään, missä neljänneksessä kulma ja kehäpiste sijaitsee. Tämän avulla voidaan päätellä onko sinα > 0 vai onko sinα < 0
Käytetään trigonometrian perusyhtälöä
Kotitehtävät: 147, 148 ja 151
Trigonometriassa tarvitaan sinin ja kosinin kaksinkertaisia kulmia, jotka määritellään
Kotitehtävät: 153, 154b ja 155
