2. Trigonometriset funktiot ja yhtälöt

Trig. funktiot

Kirjan tehtäviä: 232 eteenpäin

kotitehtävät: 236, 237 ja 240

Sini- ja kosiniyhtälö

1. Perusyhtälöt

- ovat muotoa tai muokattavissa muotoon

$\sin x=a\ \ tai\ \cos x=a{,}\ jossa\ a\ on\ vakio$

yhtälöllä on ratkaisuja vain jos -1 ≤ a ≤ 1

$Yhtälö\ \sin x=a$

- jos yhtälön yksityisratkaisu on x = α niin toinen yksityisratkaisu on x = π - α (kyseessä kehäpisteen y-koordinaatti)

Yleinen ratkaisu saadaan kun yksityisratkaisuun lisätään sinin jakso 2π (täysi kierros)

$eli\ yhtälön\ \sin x=a\ \ yleinen\ ratkaisu:\ x=\alpha+n\cdot2\pi\ tai\ x=\pi-\alpha+n\cdot2\pi$

$Yhtälö\ \cos x=a$

- jos yhtälön yksi yksityisratkaisu on x = α niin toinen ratkaisu on x = -α (kyseessä kehäpisteen x-koordinaatti)

Koska myös kosinin jaksona on 2π niin yhtälön cos x = a yleinen ratkaisu on

$x=\pm\alpha+n\cdot2\pi$

Huom!

Yksityisratkaisujen

- tarkat arvot löytyvät taulukkokirjasta

$jos\ a=0{,}\ \pm\frac{1}{2}{,}\pm\frac{\sqrt{3}}{2}{,}\pm\frac{1}{\sqrt{2}}{,}\pm1\ \left(vain\ yksi\ yksityisratkaisu\right)$

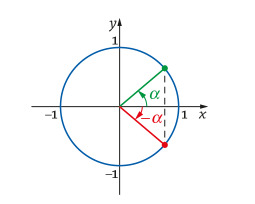
- likiarvoista toinen löytyy laskimesta ja toinen joudutaan päättelemään eli jos laskimen ratkaisu on x = α niin

siniyhtälöissä toinen yksityisratkaisu on x = π - α (asteina 180° - α) ja

kosiniyhtälöissä toinen on x = -α

Ratkaise yhtälö

$\sin x=-\frac{1}{2}$
$koska\ -\frac{1}{2}\ löytyy\ taulukosta\ niin\ yksityisratkaisut\ x\ löytyvät\ taulukosta$
$eli\ x=\frac{7\pi}{6}\ tai\ x=\frac{11\pi}{6}$
$Yleinen\ ratkaisu:\ \begin{cases} x=\frac{7\pi}{6}+n\cdot2\pi&\\ x=\frac{11\pi}{6}+n\cdot2\pi& \end{cases}n\in\mathbb{Z}\ \left(n\ on\ kok.luku\right)$

b)

$\cos3x=\frac{1}{\sqrt{2}}$

$3x=\frac{\pi}{4}+n\cdot2\pi\ \ \ tai\ \ 3x=\frac{7\pi}{4}+n\cdot2\pi\ \ \parallel:3$
$x=\frac{\pi}{12}+n\cdot\frac{2\pi}{3}\ \ tai\ x=\frac{7\pi}{12}+n\cdot\frac{2\pi}{3}$
$ko\sin iyhtälön\ tapauksessa\ vastaus\ voidaan\ esittää\ lyhyem\min$
$3x=\pm\frac{\pi}{4}+n\cdot2\pi\ \ eli\ x=\pm\frac{\pi}{12}+n\cdot\frac{2\pi}{3}$

tehtäviä: 201 →

$x=\frac{\pi}{6}+n\cdot2\pi\ \ tai$
$x=\frac{5\pi}{6}+n\cdot2\pi$

Kotitehtävät: 203, 207a ja 165

Ratkaise yhtälö

$2\sin\left(2x-\frac{\pi}{2}\right)-\sqrt{3}=0$

$Kyseessä\ on\ \sin iyhtälö\ \ 2\sin\alpha-\sqrt{3}=0{,}\ josta\ ratkaistaan\ en\sin\ mitä\ \sin\alpha\ on$
$2\sin\alpha=\sqrt{3}\ \ \parallel:2\ \ \ \Leftrightarrow\ \ \sin\alpha\ =\frac{\sqrt{3}}{2}\ \left(tarkka\ arvo\right)$
$\alpha=\frac{\pi}{3}+n\cdot2\pi\ \ tai\ \alpha=\frac{2\pi}{3}+n\cdot2\pi$
$palataan\ alkuperäiseen\ muuttujaan\ eli\ \alpha=2x-\frac{\pi}{2}$
$2x-\frac{\pi}{2}=\frac{\pi}{3}+n\cdot2\pi\ \ tai\ \ 2x-\frac{\pi}{2}=\frac{2\pi}{3}+n\cdot2\pi\ \ \left(molemmista\ ratk.\ x\right)$
$2x=\frac{\pi}{3}+\frac{\pi}{2}+n\cdot2n\ \ tai\ \ 2x=\frac{2\pi}{3}+\frac{\pi}{2}+n\cdot2n$
$2x=\frac{5\pi}{6}+n\cdot2\pi\ \ tai\ \ 2x=\frac{7\pi}{6}+n\cdot2\pi\ \ \ \parallel:2$
$x=\frac{5\pi}{12}+n\cdot\pi\ \ tai\ x=\frac{7\pi}{12}+n\cdot\pi$

208, 211, 212, 219, 220

Kotitehtävät: 213, 215 ja 220 a, c

230a

$2\sin^2x-\sin x-1=0$

kyseessä on sinx:n suhteen täydellinen toisen asteen yhtälö

$jos\ merkitään:\ \sin x=t\ niin\ yhtälö\ on\ apumuuttujan\ t\ avulla$
$2t^2-t-1=0$
$t=\frac{1\pm\sqrt{\left(-1\right)^2-4\cdot2\cdot\left(-1\right)}}{2\cdot2}=\frac{1\pm3}{4}$
$t=1\ \ tai\ t=-\frac{1}{2}$

palataan alkuperäiseen (sinx = t)

$\sin x=1\ \ \ tai\ \sin x=-\frac{1}{2}$

211, 212, 213, 219, 220, 221

Ratkaise yhtälö

$\sin^2x+\sin x=0$

Muita yhtälöitä

Ratkaise yhtälö
[[$a.\ \ 2\sin^2x-\sin x=0$]]
Kyseessä on toisen asteen yhtälö (sinx):n suhteen
[[$jos\ merkitään\ \sin x=a\ niin\ yhtälö\ on\ muotoa\ 2a^2-a=0$]]

[[$Otetaan\ \sin x\ yhteiseksi\ tekijäksi$]]
[[$\sin x\left(2\sin x-1\right)=0$]]
[[$tulon\ nollasäännön\ mukaan$]]
[[$\sin x=0\ \ tai\ 2\sin x-1=0\ \ \Leftrightarrow\ \ \sin x=\frac{1}{2}$]]
[[$\sin x=0\ \ \ \Leftrightarrow\ x=0+n\cdot2\pi=n\cdot2\pi\ \ tai\ x=\pi+n\cdot2\pi\ \ \left(lyhyem\min\ x=n\pi\right)$]]

[[$\sin x=\frac{1}{2}\ \ \Leftrightarrow\ \ x=\frac{\pi}{6}+n\cdot2\pi\ \ tai\ x=\frac{5\pi}{6}+n\cdot2\pi$]]

b.
[[$\sin2x-\cos x=0$]]
nyt
sin 2x = 2sin x cos x
[[$2\sin x\cos x-\cos x=0$]]

[[$voidaan\ ottaa\ \cos x\ yhteiseksi\ tekijäksi$]]
[[$\cos x\left(2\sin x-1\right)=0$]]
[[$\cos x=0\ tai\ \sin x=\frac{1}{2}$]]

c.
[[$\cos3x=\cos x$]]
tämä yhtälö on taulukkokirjassa olevaa muotoa

[[$\cos x=\cos y\ \ \Leftrightarrow\ \ x=\pm y+n\cdot2\pi$]]

[[$\cos3x=\cos x$]]

[[$3x=x+n\cdot2\pi\ \ tai\ 3x=-x+n\cdot2\pi$]]
[[$2x=n\cdot2\pi\ \ tai\ 4x=n\cdot2\pi$]]
[[$x=n\cdot\pi\ \ \ tai\ x=n\cdot\frac{\pi}{2}$]]

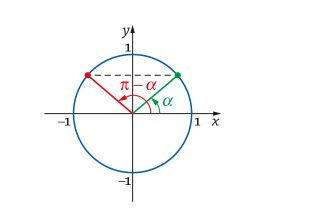
Huom! Vastaavasti jos yhtälö on muotoa sin x = sin y niin taulukkokirjasta saadaan ratkaisuidea

[[$\sin x=\sin y\ \ \Leftrightarrow\ x=y+n\cdot2\pi\ \ tai\ x=\pi-y+n\cdot2\pi$]]

Palauta vastaus

Sinulla ei ole tarvittavia oikeuksia lähettää mitään.