3.3 Derivaattafunktio

347

a) -2 -1
b) -3, 1
c)

335

A g
B f
C h

337

A1
B3
C2

358

a)
$D\left(kx\right)=k$
$\lim_{x\rightarrow a}\ \frac{kx-ka}{x-a}=\frac{k\left(x-a\right)}{x-a}=k$
b)
$D\left(k\cdot f\left(x\right)\right)=k\cdot Df\left(x\right)$
$\lim_{x\rightarrow a}=\frac{kf\left(x\right)-kf\left(a\right)}{kx-ka}=k\ \frac{f\left(x\right)-f\left(a\right)}{x-a}$

352

$f\left(x\right)=x^3+7x$

$f'\left(x\right)=3x^2+7$
$3x^2+7=0$

laskimen mukaan yhtälö on epätosi, siis yhtälön kuvaajan kasvunopeus ei ole missään kohdassa 0, eli mikään käyrälle asetetuista tangenteista ei ole vaakasuora

349

a) joo
b) ei
c) joo

348

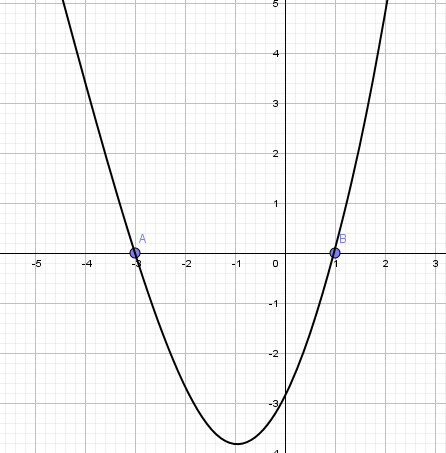
tangentti on vaakasuora, kun derivaattafunktion arvo on 0
derivoidaan paraabelin yhtälö
$f\left(x\right)=-x^2+2x+3$
$f'\left(x\right)=-2x+2$
$-2x+2=0$
$-2x=-2$

$x=1$

pisteeseen (1,0)

346

$f\left(x\right)=4x^{11}-11x^4$
$f'\left(x\right)=44x^{10}-44x^3$
$f'\left(-1\right)=44+44=88$
$g\left(x\right)=2x^{13}-13x^2$
$g'\left(x\right)=26x^{12}-26x$

$g\left(-1\right)=26+26=52$

funktion f muutosnopeus on suurempi

345

a)
$D\left(x^3-x^2-x\right)=3x^2-2x-1$
b)
$\frac{d}{dx}\left(-8x+3\right)=-8$
c)
$D\left(-5x^3-7x+1\right)=-15x^2-7$

344

a)
$f\left(x\right)=x^4$
$f'\left(x\right)=4x^3$
b)
$f\left(x\right)=x^3+1$
$f'\left(x\right)=3x^2$
c)
$f\left(x\right)=-3x$
$f'\left(x\right)=-3$

343

Voidaanko tiedosta f'(1)=2 päätellä, että funktion f derivaattafunktion kuvaaja on nouseva suora?
ei voida, se voi olla mitä vain
kuitenkin funktion f kuvaaja on nopeudella 2 nouseva suora kohdassa x=1

342

a)
$f\left(x\right)=3x^2$

$f'\left(1\right)=\lim_{x\rightarrow1}\ \frac{3x^2-3}{x-1}=\frac{3\left(x-1\right)\left(x+1\right)}{x-1}=3x+3=6$
$f'\left(a\right)=\lim_{x\rightarrow a}\ \frac{3x^2-3a}{x-a}=\frac{3\left(x-a\right)\left(x+a\right)}{x-a}=3x+3a=6a$

b)
$f'\left(x\right)=6x$
c)
$f'\left(-2\right)=6\left(-2\right)=-12$

341

a)
$D\left(2x^5-x+3\right)=10x^4-1$
b)
$D\left(4x^2+5x\right)=8x+5$
c)
$D\left(4x^7+x-1\right)=28x^6+1$

340

a)
$f\left(x\right)=-2x^3+3x^2+x$

$f'\left(x\right)=-6x^2+6x+1$

b)

$f'\left(2\right)=-24+12+1=-11$

339

a)
$f\left(x\right)=x^7$

$f'\left(x\right)=7x^6$

$f\left(x\right)=x^5+2$
$f'\left(x\right)=5x^4$
c)
$f\left(x\right)=6x$
$f'\left(x\right)=6$

338

a)
f(x)=3x
f'(x)=3
b)
$f'\left(x\right)=\lim_{x\rightarrow a}\ \frac{3x-3a}{x-a}=\lim_{x\rightarrow a}\frac{3\left(x-a\right)}{x-a}=3$

määritelmä

Funktion f derivaattafunktio on $f'$

ja $f'\left(x\right)$ on derivaatan arvo kohdassa x

$f'\left(x\right):n$ määrittelyjoukko muodostuu niistä pisteistä, joissa f on derivoituva

esim

määritä f(x) derivaattafunktio f'(x)

$f\left(x\right)=x^2$

määritetään derivaatta kohdassa a

$f'\left(a\right)=\lim_{x\rightarrow a}\frac{f\left(x\right)-f\left(a\right)}{x-a}=\lim_{\rightarrow a}\frac{x^2-a^2}{x-a}=\frac{\left(x-a\right)\left(x+a\right)}{x-a}=2a$

kohdassa a, derivaatta on 2a

kohdassa x derivaatta on 2x, eli $f'\left(x\right)=2x$

$f\left(x\right)=x^3$

$f'\left(a\right)=\lim_{x\rightarrow a}\frac{f\left(x\right)-f\left(a\right)}{x-a}=\lim_{\rightarrow a}\frac{x^3-a^3}{x-a}=\frac{\left(x-a\right)\left(x+a\right)}{x-a}=3a^2$
$f'\left(x\right)=3x^2$

$f\left(x\right)=x^4$
$f'\left(a\right)=\lim_{x\rightarrow a}\frac{f\left(x\right)-f\left(a\right)}{x-a}=\lim_{\rightarrow a}\frac{x^4-a^4}{x-a}=\frac{\left(x-a\right)\left(x+a\right)}{x-a}=4a^3$