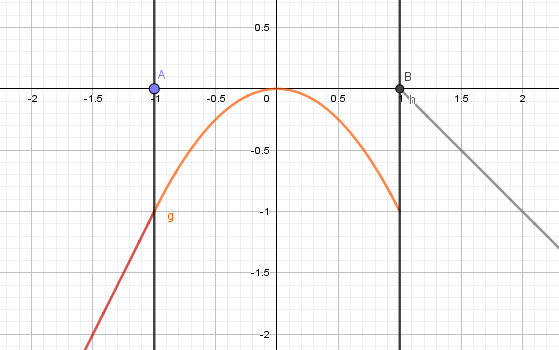
2.2 Toispuoliset raja-arvot

234

a)
a=-2
b)
$\lim_{x\rightarrow1-}=3$
$\lim_{x\rightarrow1+}=a+5$
$a+5=3$
$a=-2$

232

$f\left(x\right)=\begin{cases} 3x-6{,}&kun\ x\le6\\ \frac{x^2-36}{x-6}&kun\ x>6 \end{cases}$
$\lim_{x\rightarrow6-}=3\cdot6-6=12$
$\lim_{x\rightarrow6+}=\frac{6^2-36}{6-6}=\frac{0}{0}$

pitää sieventää

$\frac{\left(x-6\right)\left(x+6\right)}{x-6}=x+6$
$\lim_{x\rightarrow6+}=6+6=12$

raja-arvo on olemassa

231

a)
$\lim_{x\rightarrow-1-}=-1$

$\lim_{x\rightarrow-1+}=-1$

raja-arvo on olemassa kohdassa x=-1 ja se on f(x)=-1
$\lim_{x\rightarrow1-}=-1$

$\lim_{x\rightarrow1+}=0$

raja-arvoa ei ole olemassa
b)

230

a) -3
b) -3
c) -2
d) 0
e) -1
f) ei olemassa raja-arvoa, toispuoliset raja-arvot ovat erisuuret

226

a)
$x=-3$
$\lim_{x\rightarrow-3-}=f\left(-3\right)=1$

$\lim_{x\rightarrow-3+}=f\left(-3\right)=1$

$x=-1$
$\lim_{x\rightarrow-1-}=3$
$\lim_{x\rightarrow-1+}=2$
$x=1$
$\lim_{x\rightarrow1-}=2$
$\lim_{x\rightarrow1+}=2$

b) x=-1 ja x=3
c) f(-3)=1 ja f(1)=3
d) funktiota ei ole määritelty kohdassa x=3

225

$\lim_{x\rightarrow3-}=f\left(x\right)=2$

$\lim_{x\rightarrow3+}=f\left(x\right)=1$

funktiolla ei ole raja-arvoa kohdassa x=3

224

a)
$\lim_{x\rightarrow3-}=f\left(x\right)=2$
b)
$\lim_{x\rightarrow3+}=f\left(x\right)=1$
c)
funktiolla ei ole raja-arvoa kohdassa x=3, koska
$\lim_{x\rightarrow3-}\ne\lim_{x\rightarrow3+}$