4.1
417
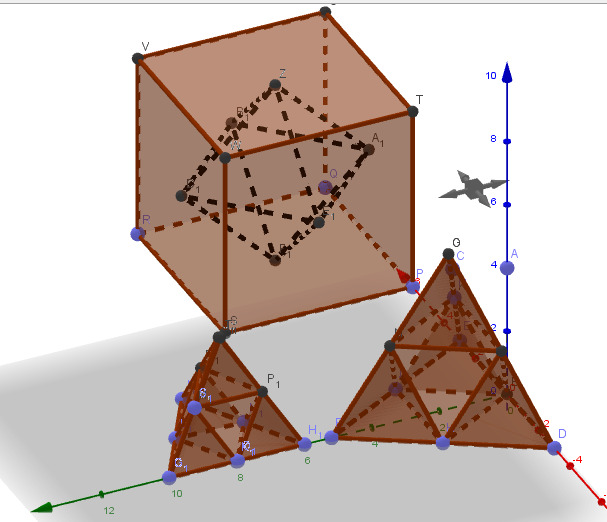
tetraedrin kaikki tahkot ovat tasasivuisia kolmioita, eli niiden kaikki kulmat ovat 60°
pohja jaetaan keskijanalla kahteen suorakulmaiseen kolmioon, lasketaan toisen pidempi kateetti kun hypotenuusa a=2 ja pienempi kateetti 



lasketaan suorakulmaisen kolmion korkeus kun pidempi kateetti on 2, lyhyempi kateetti on 
lasketaan sivusärmän ja pohjatahkon välinen kulma sinilauseella
418
414
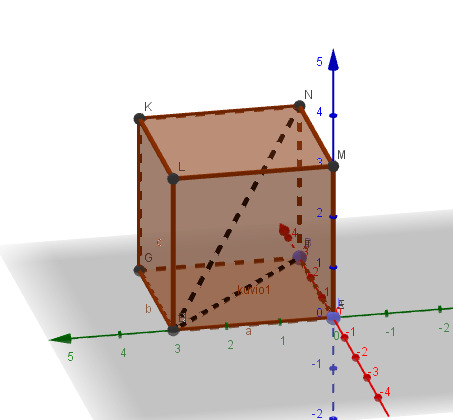
V: lasit eivät ole yhdenmuotoiset, koska tilavuuksien suhde ei ole yhtä suuri kuin mittakaavan kuutio