3.2 Derivaatan määritelmä

319

a)
$\frac{x^2-1^2}{x-1}$

b)
$\lim_{x\rightarrow1}\ \frac{x^2-1^2}{x-1}=\left(x+1\right)=2$

c) kulmakerroin on 2

321

a)
$f'\left(1\right)=\lim_{x\rightarrow1}\ \frac{3x-1}{x-1}=\lim_{x\rightarrow1}\ \frac{\left(x-1\right)3}{\left(x-1\right)}=3$
$f'\left(5\right)=\lim_{x\rightarrow5}\ \frac{3x-5}{x-5}=\lim_{x\rightarrow5}\ \frac{\left(x-5\right)3}{\left(x-5\right)}=3$
derivaatat ovat yhtäsuuret
b)

derivaatta on molempien pisteiden ja kuvaajan kautta piirrettyjen tangenttien kulmakertoimet
molemmissa 3

317

f'(2)=-3
g'(-1)=3
h'(x)=4

323

derivaatta on -3
b)
$f'\left(-2\right)=\lim_{x\rightarrow-2}\ \frac{x^2+x-2}{x+2}=\lim_{x\rightarrow-2}\ \frac{\left(x+2\right)\left(x-1\right)}{x+2}=\lim_{x\rightarrow-2}\left(x-1\right)=-2-1=-3$

määritelmä

Derivaatan määritelmä

Funktion f muutosnopeus eli derivaatta kohdassa a on $f'\left(a\right)=\lim_{x\rightarrow a}\ \frac{f\left(x\right)-f\left(a\right)}{x-a}$ , jos raja-arvo on olemassa

Tällöin f on derivoituva kohdassa a

huom lauseke $\frac{f\left(x\right)-f\left(a\right)}{x-a}$ funktion keskimääräinen muutosnopeus

Sitä kutsutaan myös erotusosamääräksi

Derivaatta on erotusosamäärän raja-arvo

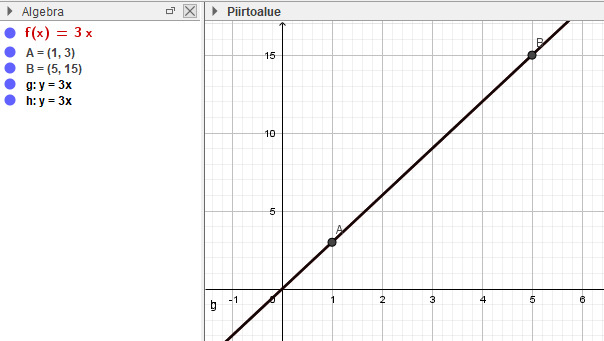
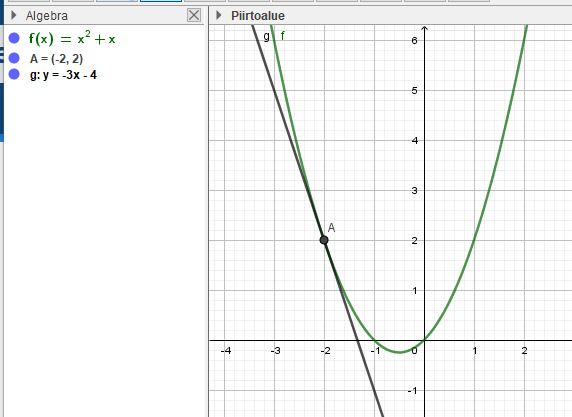
Graafisesti ajateltuna derivaatta on kuvaajalle piirretyn tangentin kulmakerroin