Tehtävät
Kertaus
K6
Autoon kohtistuvien voimien summa on tukivoiman ja painon summa

Koska auto on ilmassa, siihen ei enää vaikuttaa tukivoimaa, tällöin tukivoima
Newtonin II laen mukaan autoon kohtistuvien voimien summa on kappaleen massa ja kiihtyvyyden tull, eli

Valitaan kiihtyvyyden ja painovoiman suunta positiiviseksi, saadaan skalaari yhtälö

koska


Kun




![g=\frac{v^2}{r}\ \leftrightarrow\ v=\sqrt[]{gr}=\sqrt[]{9{,}81\ \frac{m}{s^2}\cdot45m}=21{,}0107...\approx21{,}01\frac{m}{s}](https://math-demo.abitti.fi/math.svg?latex=g%3D%5Cfrac%7Bv%5E2%7D%7Br%7D%5C%20%5Cleftrightarrow%5C%20v%3D%5Csqrt%5B%5D%7Bgr%7D%3D%5Csqrt%5B%5D%7B9%7B%2C%7D81%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%5Ccdot45m%7D%3D21%7B%2C%7D0107...%5Capprox21%7B%2C%7D01%5Cfrac%7Bm%7D%7Bs%7D)

K9
 . Koska gravitaatiovoiman suuruus on
. Koska gravitaatiovoiman suuruus on  , normaalikiihtyvyyden suurus on
, normaalikiihtyvyyden suurus on ja ilmanvastus pieni, saadaan yhtälö
ja ilmanvastus pieni, saadaan yhtälö
%5E2%7D%3Dm%5Cfrac%7Bv%5E2%7D%7B2R%7D%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft%7C%5Cright%7C%3Am)
%5E2%7D%3D%5Cfrac%7Bv%5E2%7D%7B2R%7D%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft%7C%5Cright%7C%5Ccdot2R)
 , jossa R on Maan säde
, jossa R on Maan säde
![\gamma\frac{M}{2R}=v^2\ \ \leftrightarrow\ v=\sqrt[]{\frac{\gamma M}{2R}}=\sqrt[]{\frac{6{,}67428\cdot10^{-11}\ \frac{Nm^2}{kg^2}\cdot5{,}974\cdot10^{24}kg}{2\cdot6378.140\cdot10^6m}=}5590{,}833...\ \frac{m}{s}\approx5{,}59\ \frac{km}{s}](https://math-demo.abitti.fi/math.svg?latex=%5Cgamma%5Cfrac%7BM%7D%7B2R%7D%3Dv%5E2%5C%20%5C%20%5Cleftrightarrow%5C%20v%3D%5Csqrt%5B%5D%7B%5Cfrac%7B%5Cgamma%20M%7D%7B2R%7D%7D%3D%5Csqrt%5B%5D%7B%5Cfrac%7B6%7B%2C%7D67428%5Ccdot10%5E%7B-11%7D%5C%20%5Cfrac%7BNm%5E2%7D%7Bkg%5E2%7D%5Ccdot5%7B%2C%7D974%5Ccdot10%5E%7B24%7Dkg%7D%7B2%5Ccdot6378.140%5Ccdot10%5E6m%7D%3D%7D5590%7B%2C%7D833...%5C%20%5Cfrac%7Bm%7D%7Bs%7D%5Capprox5%7B%2C%7D59%5C%20%5Cfrac%7Bkm%7D%7Bs%7D)
K11%5E2%7D%3D%5Cfrac%7B%5Cgamma100M%7D%7B100R%5E2%7D%3D%5Cfrac%7B%5Cgamma%20M%7D%7BR%5E2%7D%3D%5Cfrac%7B6%7B%2C%7D67428%5Ccdot10%5E%7B-11%7D%5C%20%5Cfrac%7BNm%5E2%7D%7Bkg%5E2%7D%5Ccdot5%7B%2C%7D974%5Ccdot10%5E%7B24%7Dkg%7D%7B%5Cleft(6378%7B%2C%7D140%5Ccdot10%5E3m%5Cright)%5E2%7D%3D9%7B%2C%7D8012...%5Capprox9.80%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D)



 , jossa M on Auringon massa
, jossa M on Auringon massa
a)
 b)
b)
Autoon kohtistuvien voimien summa on tukivoiman ja painon summa
Koska auto on ilmassa, siihen ei enää vaikuttaa tukivoimaa, tällöin tukivoima
Newtonin II laen mukaan autoon kohtistuvien voimien summa on kappaleen massa ja kiihtyvyyden tull, eli
Valitaan kiihtyvyyden ja painovoiman suunta positiiviseksi, saadaan skalaari yhtälö
koska
Kun
K9
a)
Voidaan käyttää Newtonin gravitaatiovoiman kaava
b)
Newtonin toisen lain mukaan Nopeus on
K11
Gravitaatiokent'n voimakkuus saadaan kaavasta
K12
Newtonin II lain mukaan  , koska gravitaatiovoiman suuruus on
, koska gravitaatiovoiman suuruus on  , normaalikiihtyvyyden suuruus on
, normaalikiihtyvyyden suuruus on  ja ilmavastus on pieni, voidaan muodosta yhtälö
ja ilmavastus on pieni, voidaan muodosta yhtälö
Auringon massa on
%5E2%7D%7B6%7B%2C%7D67428%5Ccdot10%5E%7B-11%7D%5C%20%5Cfrac%7BNm%5E2%7D%7Bkg%5E2%7D%7D%3D1%7B%2C%7D98818...%5Ccdot10%5E%7B30%7Dkg%5Capprox1%7B%2C%7D988%5Ccdot10%5E%7B30%7Dkg)
K15a)
Jaksoaika:
Taajuus:
Jaksoaika:

Taajuus:

Taajuus:
Kpl.15
15-2

%5E2%3D5%7B%2C%7D5417...%5Ccdot10%5E%7B-11%7D%3D5%7B%2C%7D5%5Ccdot10%5E%7B-11%7DW)









Tehtävässä pitää laskea mikä on se toinen etäisyys, eli , joten muutetaan alkuperäisen kaavan tehää muotoon
, joten muutetaan alkuperäisen kaavan tehää muotoon
![\frac{I_1}{I_2}=\frac{r_2^2}{r_1^2}\ \leftrightarrow\ r_2=\sqrt[]{\left(r_1^2\cdot\frac{I_2}{I_1}\right)}=\sqrt[]{1^2m\cdot\frac{10^0\ \frac{W}{m^2}}{10^{-9}\ \frac{W}{m^2}}}=31622{,}7766m=31{,}6227766km\approx32km](https://math-demo.abitti.fi/math.svg?latex=%5Cfrac%7BI_1%7D%7BI_2%7D%3D%5Cfrac%7Br_2%5E2%7D%7Br_1%5E2%7D%5C%20%5Cleftrightarrow%5C%20r_2%3D%5Csqrt%5B%5D%7B%5Cleft(r_1%5E2%5Ccdot%5Cfrac%7BI_2%7D%7BI_1%7D%5Cright)%7D%3D%5Csqrt%5B%5D%7B1%5E2m%5Ccdot%5Cfrac%7B10%5E0%5C%20%5Cfrac%7BW%7D%7Bm%5E2%7D%7D%7B10%5E%7B-9%7D%5C%20%5Cfrac%7BW%7D%7Bm%5E2%7D%7D%7D%3D31622%7B%2C%7D7766m%3D31%7B%2C%7D6227766km%5Capprox32km)
Ihmisen kuuloalue kuvaajan mukaan 100 dB:n intensitettitasoa vastaa intensiteetti
Äänen teho saadan kaavalla
15-4
Jos ääni etenee vapaasti kaikkii suuntiin, on kahdella etäisyydellä ja
ja mitattujen intensiteettien suhde on
mitattujen intensiteettien suhde on
Tehtävässä pitää laskea mikä on se toinen etäisyys, eli  , joten muutetaan alkuperäisen kaavan tehää muotoon
, joten muutetaan alkuperäisen kaavan tehää muotoon
![\frac{I_1}{I_2}=\frac{r_2^2}{r_1^2}\ \ \leftrightarrow\ r_2=\sqrt[]{\left(r_1^2\cdot\frac{I_1}{I_2}\right)}=\sqrt[]{12^2m\cdot\ \frac{10^{-4}\ \frac{W}{m^2}}{1{,}0\ \frac{W}{m^2}}}=0{,}12m](https://math-demo.abitti.fi/math.svg?latex=%5Cfrac%7BI_1%7D%7BI_2%7D%3D%5Cfrac%7Br_2%5E2%7D%7Br_1%5E2%7D%5C%20%5C%20%5Cleftrightarrow%5C%20r_2%3D%5Csqrt%5B%5D%7B%5Cleft(r_1%5E2%5Ccdot%5Cfrac%7BI_1%7D%7BI_2%7D%5Cright)%7D%3D%5Csqrt%5B%5D%7B12%5E2m%5Ccdot%5C%20%5Cfrac%7B10%5E%7B-4%7D%5C%20%5Cfrac%7BW%7D%7Bm%5E2%7D%7D%7B1%7B%2C%7D0%5C%20%5Cfrac%7BW%7D%7Bm%5E2%7D%7D%7D%3D0%7B%2C%7D12m)


15-6
Laketaan äänen intensiteettitasoa kaavalla
15-7
 Kymmenen lehtipuhaltimen äänen intensiteettitaso on
Kymmenen lehtipuhaltimen äänen intensiteettitaso on
 jaintensiteettitaso on
jaintensiteettitaso on

(MAOL s.91) Ihmisen kuuloalue kuvaajan mukaan 100 dB:n intensitettitasoa vastaa intensiteetti
15-9
(MAOL s.91) Ihmisen kuuloalue kuvaajan mukaan 120 dB:n intensiteettitasoa vastaa intensiteetti
ja 130 Hz:n intensiteettitasoa vastaa intensiteetti
Jos ääni etenee vapaasti kaikkii suuntiin, on kahdella etäisyydellä ja
ja mitattujen intensiteettien suhde on
mitattujen intensiteettien suhde on
Tehtävässä pitää laskea mikä on se toinen etäisyys, eli
Kpl.14
14-1
Huilun sävel riippuu siitä ulottuvan äänen taajuudesta
Taajuutta voidaan saada kaavalla
Poikkihuiluun syntyvän perussävelen taajuudeksi saadaan
Koska poikkihuiluun syntyvän perussävelen taajuus on pienempi, tällöin ääniaallot ovat asetettu tiheämmin, näin ollen poikkihuiluun syntyvän perussävelen on korkeampi.
14-3
Aallonpituutta voidaan laskea kaavalla
Koska bassoklarinetti on puoleksi suljettu putki, sen pituus on lambdan kanssa suhteessa
14-4
a)
Perussävel:
Ensimmäinen yläsävel:
b)



Perussävel:
Jos on toisesta päästä suljettu putki, aallonpituus olisi tällöin









Jos on toisesta päästä suljettu putki, aallonpituus olisi tällöin
Ensimmäinen yläsävel:
Jos on toisesta päästä suljettu putki, aallonpituus olisi tällöin

14-5
tai
14-8
a)
b)
Jos pillissä on ilman sijasta heliumia, äänen nopeus olisi tällöin
Kpl.13
13-3



c)

%3D32%7B%2C%7D731...%5Capprox32%7B%2C%7D73%C2%B0)


)
)


 b)
b)

13-10
a)
b)
c)
13-6
a) Sukellusveneen potkuri lähettää koko ajan 45 Hz:n ääntä, joten äänen taajuus ei muutu. Aaltoliikkeen perusyhtälö on v = fλ. Koska äänen nopeus v pienenee ja taajuus f ei muutu rajapinnan ylittämisen jälkeen, ääniaallon aallonpituuden λ täytyy pienentyä.
b)
Koska äänen nopeus pienenee rajapinnan ylityksen jälkeen, ääniaaltojen etenemissuunta kääntyy normaaliin päin. Siten kokonaisheijastuminen ei ole mahdollinen. Näin ääniaallolle ovat mahdollisia kaikki tulokulman α1 arvot 0 ≤ α1 < 90°, ja ääni läpäisee veden ja ilman rajapinnan.
13-7
Äänen nopeus 20°C:ssa vedessä on 1484 m/s ja 343 m/s ilmassa (Maol)
Nopeuden kaavan mukaan
Koska etäisyys on sama, voidaan muodosta yhtälön
13-9
a)
13-10
Kpl.12
12-2
a)
a)
Lasketaan ensi mikä on aallonpituus
Yhden kuvun pituus on yhtä kuin aallonpituuden puolikas, joten:
Kupuja on 5
b)
Jos taajust olisi 3,2 Hz, uusi aallonpituus olisi
ja yhden kuvun pituus olisi
Kupuja on 4
12-3
a)
b)
c)
12-5
a) Kumiletkun toinen pää on kiinni seinässä ja toinen pää A jää paikalleen, joten molemmissa päissä on solmukohta. Lisäksi seinän ja pisteen A välissä on kaksi solmua. Solmukohtia on siis yhteensä 4 ja kupuja tulee 3.
Piirretään kuva tilanteeseta
b)
12-6
a)
2,5 aallonpituutta
b)
0,47m
c)
4
d)
12-9




a)
b)
Kielen perusvärähtelyssä on kaksi solmua ja yksi kupu, ensimmäisessä ylävärähtelyssä on kolme solmua ja kaksi kupua, joten toisessa on neljä solmua ja kolme kupua.
c)12-11
a) Koska kiinnityskohdissa lanka ei pääse vapaasti värähtelemään, kiinnityskohtiin muodostuu solmut.
b) Perustaajuus  vastaa yksinkertaisinta mahdollista seisovan aallon tilannetta. Silloin lankaan muodostuu yksi kupu ja molempiin päihin solmut. Langan pituus on aallonpituuden puolikas: l = λ/2, josta aallonpituudeksi saadaan λ = 2l = 2 ∙ 0,50 m = 1,0 m
vastaa yksinkertaisinta mahdollista seisovan aallon tilannetta. Silloin lankaan muodostuu yksi kupu ja molempiin päihin solmut. Langan pituus on aallonpituuden puolikas: l = λ/2, josta aallonpituudeksi saadaan λ = 2l = 2 ∙ 0,50 m = 1,0 m
c) Värähtelytaajuus on perustaajuuteen verrattuna 4-kertainen eli f = 4 ∙ f0. Lankaan muodostuu 4 aallonpituuden puolikasta ja siksi 4 kupua ja 5 solmua. Langan pituus on , jostaaallonpituudeksi saadaan
, jostaaallonpituudeksi saadaan 
c) Värähtelytaajuus on perustaajuuteen verrattuna 4-kertainen eli f = 4 ∙ f0. Lankaan muodostuu 4 aallonpituuden puolikasta ja siksi 4 kupua ja 5 solmua. Langan pituus on
Kpl.11
11-1
A 3
11-2
a,c,d,f
11-4
Diffraktion takia vesiaalto on tapunut raon kohdalla, ja se taippuu suoraaallosta ympyrämuotoiseksi aalloksi.
11-8
1,0s
1,0s
11-10
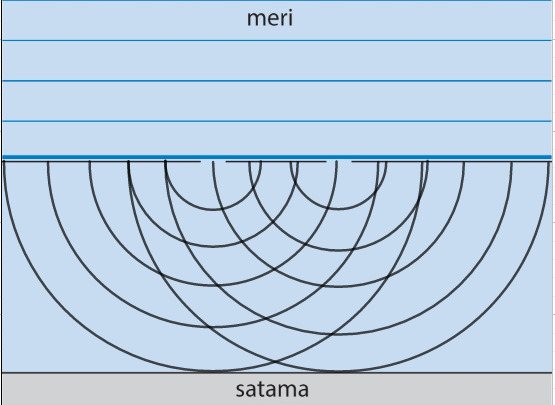
a) Kun vesiaalto saappuu satama-altaaseen, aalto kimpaa diffraktion vaikutuksesta mereenpäin diffraktion ja tästä syntyy uusi aalto, ja satama-altaan raoista aallto pääsee siitä etenemään, tästäkin syntyy uusi aalto. Uusi aalto saattaa osua edellistä aaltoa, ja tämä on interferenssi.
Kpl.10
10-2
a) Kun aalto taittuu, taajuus ei muutu, koska aaltoliikkeen taajuus riippuu vain aallon lähteestä.
HUOM. Tajuu ei muutu myöskään aallon heijastuessa aineiden rajapinnasta.
b) Koska aalto taittuu normaaliin päin, aallon nopeus pienenee.
c) Koska aalto taittu normaaliin päin, aallon aallonpituus pienenee
HUOM. c-kohdan voi perusteella myös aaltoliikkeen perusyhtälön avulla
10-4
a)
Taittumislaista  saadaan
saadaan
b)
Taittumislaista  saadaan
saadaan
10-5
a)
Koska taitesuhde on 1,9
b)
Taittumislaista  saadaan
saadaan
10-11
a)
Aaltoliikkeen perusyhtälön  mukaan vesiaaltojen nopeus ennen estettä on
mukaan vesiaaltojen nopeus ennen estettä on 
b)
Vesiaaltojen taajuuden määrää aaltolähde, joten taajuus on sama ennen estettä ja esteen päällä eli c)c)
Aaltoliikkeen taittumislaki
Kpl.9
9-1









a) Ei muuttuu
b) Kaksinkertaistuu
c) Kun aallonpituus puolittuu, nopeuskin puolittuu
9-5
9-6
9-8
a)
b)
c)
d)
Kpl.8
8-4


![T=2\pi\sqrt[]{\frac{m}{k}}=2\pi\sqrt[]{\frac{0{,}17kg}{16\ \frac{N}{m}}}=0{,}6476...\approx0{,}65s](https://math-demo.abitti.fi/math.svg?latex=T%3D2%5Cpi%5Csqrt%5B%5D%7B%5Cfrac%7Bm%7D%7Bk%7D%7D%3D2%5Cpi%5Csqrt%5B%5D%7B%5Cfrac%7B0%7B%2C%7D17kg%7D%7B16%5C%20%5Cfrac%7BN%7D%7Bm%7D%7D%7D%3D0%7B%2C%7D6476...%5Capprox0%7B%2C%7D65s)



![T=2\pi\sqrt[]{\frac{0{,}350kg}{24{,}525\ \frac{N}{m}}}=0{,}7506...\approx0{,}75s](https://math-demo.abitti.fi/math.svg?latex=T%3D2%5Cpi%5Csqrt%5B%5D%7B%5Cfrac%7B0%7B%2C%7D350kg%7D%7B24%7B%2C%7D525%5C%20%5Cfrac%7BN%7D%7Bm%7D%7D%7D%3D0%7B%2C%7D7506...%5Capprox0%7B%2C%7D75s)



![T=2\pi\sqrt[]{\frac{m}{k}}](https://math-demo.abitti.fi/math.svg?latex=T%3D2%5Cpi%5Csqrt%5B%5D%7B%5Cfrac%7Bm%7D%7Bk%7D%7D)
![\frac{T}{2\pi}=\sqrt[]{\frac{m}{k}}](https://math-demo.abitti.fi/math.svg?latex=%5Cfrac%7BT%7D%7B2%5Cpi%7D%3D%5Csqrt%5B%5D%7B%5Cfrac%7Bm%7D%7Bk%7D%7D)
%5E2%3D%5Cfrac%7Bm%7D%7Bk%7D)
%5E2%7D%3D%5Cfrac%7B0%7B%2C%7D500kg%7D%7B%5Cleft(%5Cfrac%7B1%7B%2C%7D0989s%7D%7B2%5Cpi%7D%5Cright)%5E2%7D%3D16%7B%2C%7D346...%5Capprox16%7B%2C%7D35%5C%20%5Cfrac%7BN%7D%7Bm%7D)






a)
880 kertaa
b)
8-5
8-6
Koska kappale on kiinnitetty jouseen, siihen kohdistuva voima F on suunta ylös ja painovoima G alas.
Newtonin II lain nojallla saadaan yhtälön eli
eli . Koska
. Koska  ,
, 
Valitaan suunta alas positiiviseksi, koska sekä  että
että  ovat positiivisia
ovat positiivisia
Yhtälö saadaan, muotoon
Värähtelyn jaksonaika saadaan kaavalla
8-7
a)
B
b)
A
c)
C
8-8
a)
0,91Hz
b)
Otetaan testipisteeksi pisteet (0,3;0,03) ja (0,2;-0,04)
c)
d) Kuvaajan kärkikohdassa.
8-10
a)
0,67s
b)
c)
d)
Kpl.7
7-3



7-5
a)
b)
7-5
a)
Löysempi
b)
Jäykämpi
c)
Jousivoima 
Jousivoima ja poikkeama ovat vastakkaisuuntaisia, joten ottamalla suunnat huomioon ,saadaan  ja tästä saadaan jousivakioksi
ja tästä saadaan jousivakioksi 
Kun jousi katkaistaan keskeltä, on venymä x/2. Tällöin 
7-6
a)
Jousta puristava voima on -1,7N. Jousivoima  ja puristava voima ovat yhtä suuret.Mutta vastakkaissuuntaiset, joten jousivoima on
ja puristava voima ovat yhtä suuret.Mutta vastakkaissuuntaiset, joten jousivoima on 
Koska jousivoima  , niin jousivakio on
, niin jousivakio on
Newtonin II-lain mukaan 
Kun vaunu päästetään irti, vaikuttaa siihen tason suunnassa ainoastaan jousvoima, koska kitkaa ja ilmanvastusta ei oteta huomioon. (Pystysuunnassa vaunulla ei ole kiihtyvyyttä)
Näin ollen  . Kiihtyvyys on
. Kiihtyvyys on 
a) Tasapainoasemassa x=0,00m, jousivoima on nolla, joten kiihtyvyys on 
b) Hetki ennen vaunun irtipäästöä jousta puristava voima ja jousivoima ovat yhtä suuret ja vastakkaisuuntaiset. Vaunnu lähtee liikkeelle ääriasennosta ja sen kiihtyvyys ja jousivoima ovat samansuuntaiset. Vaunun kiihtyvyys on
c) x=0,12m
Vaunu on ohttanut tasapainoaseman. Jousivoima suuntautuu kohti tasapainoasemaa. Vaunun kiihtyvyys on
Vaunu on kiihtyvässä liikkeessä kohti tasapainoasemaa tai hidastuvassa liikeessä alkuperäoseen positiiviseen liikesuuntaan nähden.
Kpl.6
6-1
a)
Lasketaan avaruusaseman ratanopeus
Gravitaatiovuorovaikutus pitää sateliitin radallaan. Newtonin II lain mukaan on  , jossa gravitaatiovoiman suuruus on
, jossa gravitaatiovoiman suuruus on  ja normaalikiihtyvyyden suuruus
ja normaalikiihtyvyyden suuruus  . Yhtälöstä
. Yhtälöstä  ratanopeudeksi saadaan
ratanopeudeksi saadaan
b)
c)
6-2
m=satelliitin massa, M=Maan massa
r=Sateliitin etäisyys Maan keskipisteestä
Sateliitin liike-energia on  , missä v=satelliitin ratanopeus
, missä v=satelliitin ratanopeus
Newtonin II-lain mukaan
Gravitaatiovuorovaikutus pitää satelliitin radallaan
Gravitaatiovoima on  ja normaalikiihtyvyys on
ja normaalikiihtyvyys on 
Ratkaistaan sateliitin ratanopeuden neliö yhtälöstä
b)
6-4
a)

-%5Cleft(-%5Cgamma%5Ccdot%5Cfrac%7BmM%7D%7Br_1%7D%5Cright)%3D-%5Cgamma%5Ccdot%5Cfrac%7BmM%7D%7Br_2%7D%2B%5Cgamma%5Ccdot%5Cfrac%7BmM%7D%7Br_1%7D%3D-%5Cgamma%20mM%5Ccdot%5Cleft(%5Cfrac%7B1%7D%7Br_2%7D-%5Cfrac%7B1%7D%7Br_1%7D%5Cright))
)



6-6

%3D%5Cfrac%7B1%7D%7B2%7Dmv_l%5E2%2B%5Cleft(-%5Cgamma%5Cfrac%7BmM%7D%7Brl%7D%5Cright))
%3D%5C%20-%5Cgamma%5Cfrac%7BmM%7D%7Br%7D)

%5E2%3D15%5C%20108%5C%20736m%5Capprox15%5C%20108%7B%2C%7D7%5C%20km%7D)
b)
6-6
6-8
Kaikki oikein
Kaikki oikein
Kpl.5
5-2



%5E2%7D%7B149%7B%2C%7D59787%5Ccdot10%5E6km%7D%3D5%7B%2C%7D928...%5Ccdot10%5E%7B-3%7D%5Capprox5%7B%2C%7D93%5Ccdot10%5E%7B-3%7D%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D)



%5E2%7D%7B384%5C%20400%5C%20000m%7D%3D2%7B%2C%7D7225%5Ccdot10%5E%7B-3%7D%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D)
5-4






![v^2=\frac{\gamma M}{r}\ \ \ \ \ \left|\right|\sqrt[]{}](https://math-demo.abitti.fi/math.svg?latex=v%5E2%3D%5Cfrac%7B%5Cgamma%20M%7D%7Br%7D%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft%7C%5Cright%7C%5Csqrt%5B%5D%7B%7D)
![v=\sqrt[]{\frac{\gamma M}{r}}=1018{,}46\ \frac{m}{s}=1{,}018\ \frac{km}{s}](https://math-demo.abitti.fi/math.svg?latex=v%3D%5Csqrt%5B%5D%7B%5Cfrac%7B%5Cgamma%20M%7D%7Br%7D%7D%3D1018%7B%2C%7D46%5C%20%5Cfrac%7Bm%7D%7Bs%7D%3D1%7B%2C%7D018%5C%20%5Cfrac%7Bkm%7D%7Bs%7D)

5-5

%5E2%5Ccdot9%5C%20370%5C%20000m%7D%7B6%7B%2C%7D67428%5Ccdot10%5E%7B-11%7D%5C%20%5Cfrac%7BNm%5E2%7D%7Bkg%5E2%7D%7D%5Capprox6%7B%2C%7D42%5Ccdot10%5E%7B23%5C%20kg.%7D)
5-6
![v=\sqrt[]{\frac{\gamma M}{r}}=\sqrt[]{\frac{6{,}67428\cdot10^{-11}\ \frac{Nm^2}{kg^2}\cdot5{,}974\cdot10^{24}kg}{6378km+610km}}=7553{,}68\ \frac{m}{s}\approx7{,}6\ \frac{km}{s}](https://math-demo.abitti.fi/math.svg?latex=v%3D%5Csqrt%5B%5D%7B%5Cfrac%7B%5Cgamma%20M%7D%7Br%7D%7D%3D%5Csqrt%5B%5D%7B%5Cfrac%7B6%7B%2C%7D67428%5Ccdot10%5E%7B-11%7D%5C%20%5Cfrac%7BNm%5E2%7D%7Bkg%5E2%7D%5Ccdot5%7B%2C%7D974%5Ccdot10%5E%7B24%7Dkg%7D%7B6378km%2B610km%7D%7D%3D7553%7B%2C%7D68%5C%20%5Cfrac%7Bm%7D%7Bs%7D%5Capprox7%7B%2C%7D6%5C%20%5Cfrac%7Bkm%7D%7Bs%7D)
%7D%7B7553%7B%2C%7D68%5C%20%5Cfrac%7Bm%7D%7Bs%7D%7D%3D5812%7B%2C%7D65s%5Capprox97%5Cmin)

5-12
a)
b)
5-4
Maan massa on 
Kuun massa on 
Maan ja kuun keskietäisyys
a) Gravitaatiovuorovaikutus pitää Kuun Maata kiertävällä radalla, joka voidaan mallintaa ympyräratana
Newtonin II-lain mukaan
Sijoittaalla saadaan
b) Koska Kuu on ympyräradalla, yksi kierros on pituudeltaan 2πr.
Siten kierrtoaika on
5-5
a)
Sateliitin kiertoaika planeetan ympäri on 7h39min=27540s
Sateliitin kiertoradan pituus on  ja ratanopeus
ja ratanopeus
Gravitaatiovuorovaikutus pitää sateliitin radallaan . Newtonin II lain mukaan  , jossa gravitaatiovoiman suuruus on
, jossa gravitaatiovoiman suuruus on  ja normaalikiihtyvyyden suuruus
ja normaalikiihtyvyyden suuruus  . Yhtälöstä
. Yhtälöstä  planeetan massaksi saadaan
planeetan massaksi saadaan
5-6
Gravitaatiovuorovaikutus pitää sateliitin radallaan. Newtonin II lain mukaan on  , jossa gravitaatiovoiman suuruus on
, jossa gravitaatiovoiman suuruus on  ja normaalikiihtyvyyden suuruus
ja normaalikiihtyvyyden suuruus  . Yhtälöstä
. Yhtälöstä  ratanopeudeksi saadaan
ratanopeudeksi saadaan
b) kiertoaika Maan ympäri on
c) Kulmanopeus on
5-12
a)
Epätosi
b)
Tosi
c)
Tosi
d)
Tosi
Kpl.4
4-2
Vaikka astronautti tuntee itensä painottomaksi, häneen ja avaruusalukseen kohdistuu man vetovoima. sillä avanruusalus pysyy maata kiertävällä radalla. Eäisyys on kuitenkin sen verrean suuri, että avaruusalus ei putoa maahan ja sen verran pieni, ettei avaruusaluus leijaile ulkoavaruuteen.
4-5



%5E2%7D%3D9%7B%2C%7D7955377...%5Capprox9%7B%2C%7D80%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D)

%5E2%7D%3D9%7B%2C%7D779...%5Capprox9%7B%2C%7D78%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D)
4-6




4-8





Vaikka astronautti tuntee itensä painottomaksi, häneen ja avaruusalukseen kohdistuu man vetovoima. sillä avanruusalus pysyy maata kiertävällä radalla. Eäisyys on kuitenkin sen verrean suuri, että avaruusalus ei putoa maahan ja sen verran pieni, ettei avaruusaluus leijaile ulkoavaruuteen.
4-5
a)
b)
c)
Pienenee
4-6
a)
b)
53kg
4-8
Gravitaatiokentän voimakkuus neutronitähden pinnalla on
Tähden massa on 
Oletetaan tähti pallon muotoiseksi, jolloin sen tilavuus on 
4-9






![g=\gamma\ \cdot\frac{M}{r^2}\ \leftrightarrow\ r=\sqrt[]{\frac{\gamma M}{g}}](https://math-demo.abitti.fi/math.svg?latex=g%3D%5Cgamma%5C%20%5Ccdot%5Cfrac%7BM%7D%7Br%5E2%7D%5C%20%5Cleftrightarrow%5C%20r%3D%5Csqrt%5B%5D%7B%5Cfrac%7B%5Cgamma%20M%7D%7Bg%7D%7D)
![r=\sqrt[]{\frac{\gamma M}{g}}=\sqrt[]{\frac{6{,}67428\cdot10^{-11}\frac{Nm^2}{kg^2}\cdot5{,}974\cdot10^{24}kg}{4{,}903325\ \frac{m}{s^2}}}=9017638{,}095m](https://math-demo.abitti.fi/math.svg?latex=r%3D%5Csqrt%5B%5D%7B%5Cfrac%7B%5Cgamma%20M%7D%7Bg%7D%7D%3D%5Csqrt%5B%5D%7B%5Cfrac%7B6%7B%2C%7D67428%5Ccdot10%5E%7B-11%7D%5Cfrac%7BNm%5E2%7D%7Bkg%5E2%7D%5Ccdot5%7B%2C%7D974%5Ccdot10%5E%7B24%7Dkg%7D%7B4%7B%2C%7D903325%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%7D%7D%3D9017638%7B%2C%7D095m)

4-12
![g_r=\gamma\frac{M}{r^2}\ \leftrightarrow r=\sqrt[]{\frac{\gamma M}{g_r}}](https://math-demo.abitti.fi/math.svg?latex=g_r%3D%5Cgamma%5Cfrac%7BM%7D%7Br%5E2%7D%5C%20%5Cleftrightarrow%20r%3D%5Csqrt%5B%5D%7B%5Cfrac%7B%5Cgamma%20M%7D%7Bg_r%7D%7D)
![\left[r\right]=\sqrt[]{\frac{\left[\gamma\right]\left[M\right]}{\left[g\right]}}=\sqrt[]{\frac{1\ \frac{Nm^2}{kg^2}\cdot1kg}{1\ \frac{m}{s^2}}}=\sqrt[]{\frac{1\ \frac{\mathrm{\frac{kgm}{s^2}\cdot m^2}}{kg^2}\cdot1kg}{1\ \frac{m}{s^2}}}=\sqrt[]{\frac{1\ \frac{m^2}{s^2}}{1\ \frac{m}{s^2}}}=\sqrt[]{1\ m^2}=1m](https://math-demo.abitti.fi/math.svg?latex=%5Cleft%5Br%5Cright%5D%3D%5Csqrt%5B%5D%7B%5Cfrac%7B%5Cleft%5B%5Cgamma%5Cright%5D%5Cleft%5BM%5Cright%5D%7D%7B%5Cleft%5Bg%5Cright%5D%7D%7D%3D%5Csqrt%5B%5D%7B%5Cfrac%7B1%5C%20%5Cfrac%7BNm%5E2%7D%7Bkg%5E2%7D%5Ccdot1kg%7D%7B1%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%7D%7D%3D%5Csqrt%5B%5D%7B%5Cfrac%7B1%5C%20%5Cfrac%7B%5Cmathrm%7B%5Cfrac%7Bkgm%7D%7Bs%5E2%7D%5Ccdot%20m%5E2%7D%7D%7Bkg%5E2%7D%5Ccdot1kg%7D%7B1%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%7D%7D%3D%5Csqrt%5B%5D%7B%5Cfrac%7B1%5C%20%5Cfrac%7Bm%5E2%7D%7Bs%5E2%7D%7D%7B1%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%7D%7D%3D%5Csqrt%5B%5D%7B1%5C%20m%5E2%7D%3D1m)
4-12
Yksikkötarkastelu
Kpl.3
3-4
Ganymedes:n kiertoaika on x
%5E2%7D%7Bx%5E2%7D%3D%5Cfrac%7B%5Cleft(4%5Ccdot10%5E8m%5Cright)%5E3%7D%7B%5Cleft(11%5Ccdot10%5E8m%5Cright)%5E3%7D)
%5E2%5Ccdot%5Cleft(11%5Ccdot10%5E8m%5Cright)%5E3%3Dx%5E2%5Ccdot%5Cleft(4%5Ccdot10%5E8m%5Cright)%5E3)
%5E2%5Ccdot%5Cleft(11%5Ccdot10%5E8m%5Cright)%5E3%7D%7B%5Cleft(4%5Ccdot10%5E8m%5Cright)%5E3%7D)
%5E2%5Ccdot%5Cleft(11m%5Cright)%5E3%7D%7B%5Cleft(4m%5Cright)%5E3%7D)
![x=\sqrt[]{\frac{\left(1{,}8d\right)^2\cdot\left(11m\right)^3}{\left(4m\right)^3}}](https://math-demo.abitti.fi/math.svg?latex=x%3D%5Csqrt%5B%5D%7B%5Cfrac%7B%5Cleft(1%7B%2C%7D8d%5Cright)%5E2%5Ccdot%5Cleft(11m%5Cright)%5E3%7D%7B%5Cleft(4m%5Cright)%5E3%7D%7D)





%5E2%7D%3D4%7B%2C%7D134...%5Ccdot10%5E%7B-13%7D%5Capprox4%7B%2C%7D1%5Ccdot10%5E%7B-13%7DN)
3-6
a) Koska Maalla on suurempi massa
b) Koska Auringolla suurempi massa
3-9
a)
b)
Koska palloihin vaikuttaa ainoastaan gravitaatiovoima

Koska palloihin vaikuttaa ainoastaan gravitaatiovoima
3-12
Olkoon Maan ja Auringon välissä kappale, jonka massa on m.Kappale sijaitsee Maan ja Aurigon välissä kohdasssa, jossa vetovoimat ovat yhtä suuret. Olkoon x kysytty etäisyys Maan keskipisteestä lähtien.

%5E%7B%5E2%7D%7D)
%5E%7B%5E2%7D%7D%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft%7C%5Cright%7C%3A%5Cgamma)
%5E2%7D%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft%7C%5Cright%7C%3Am)
%5E2%7D)
![x=\frac{-\left(\sqrt[]{m_1m_2}-m_1\right)r}{m_1-m_2}](https://math-demo.abitti.fi/math.svg?latex=x%3D%5Cfrac%7B-%5Cleft(%5Csqrt%5B%5D%7Bm_1m_2%7D-m_1%5Cright)r%7D%7Bm_1-m_2%7D)
Olkoon Maan ja Auringon välissä kappale, jonka massa on m.Kappale sijaitsee Maan ja Aurigon välissä kohdasssa, jossa vetovoimat ovat yhtä suuret. Olkoon x kysytty etäisyys Maan keskipisteestä lähtien.
Maan ja kappaleen välinen gravitaatiovoima on
Auringon ja kappaleen välinen etäisyys on  ja gravitaatiovoima on
ja gravitaatiovoima on
Kappaleeseen vaikuttaa yhtä suuri Maan ja Auringon vetovoima eli 
Ratkaise Etäisyys x yhtälöllä
Kpl.2
2-3
a) Gravitaati voima
b) Istuimen ketjujen jännitysvoima, kitka
c) Lepokitka
2-4
a) Tosi
b) Epätosi
c) Epätosi
2-5
V: A:ssa on suurempi



 eli
eli  . Koska sekä kitka että normaalikiihtyvyys suuntautuvat kohti ympyräradan keskipistettä, yhtälöstä
. Koska sekä kitka että normaalikiihtyvyys suuntautuvat kohti ympyräradan keskipistettä, yhtälöstä  eli
eli  saadaan kitkakertoimeksi
saadaan kitkakertoimeksi
%5E2%7D%7B22m%5Ccdot9%7B%2C%7D81%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%7D%3D0%7B%2C%7D1158372718)
2-6
a)
Koska ilmavastus on pieni, autoon vaikuttava kokonaisvoima on  . Koska pinta on vaakasuora, pinnan tukivoima
. Koska pinta on vaakasuora, pinnan tukivoima  ja autoon kohdistuva paino
ja autoon kohdistuva paino ovat yhtä suuret ja vastakkaisuunatiset, joten ne kumoavat toisensa. Kitka
ovat yhtä suuret ja vastakkaisuunatiset, joten ne kumoavat toisensa. Kitka  pitää auton ympyräradalla. Newtonin II lain mukaan jään pinnan suunnassa on
pitää auton ympyräradalla. Newtonin II lain mukaan jään pinnan suunnassa on
b)
Pysyy, koska saattu kitka on suurempi kuin 1,4kN
2-9
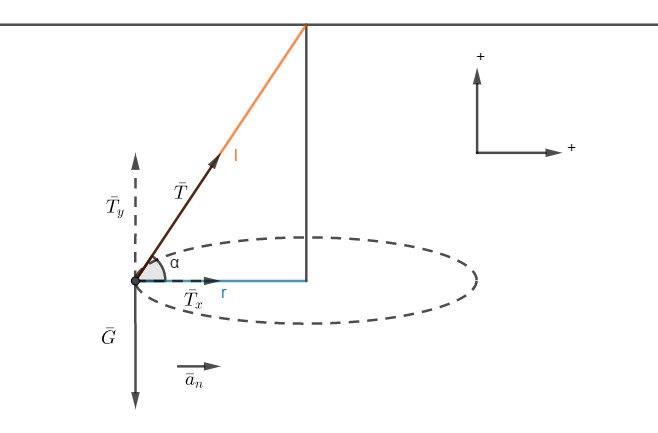
a)
Oletetaan ilmanvastus pieneksi.
Koneeseen vaikuttavat voimat ovat langan jännitysvoima  ja paino
ja paino 
Langan jännitysvoiman vaakasuuntaan komponentti itä koneen ympyräradalla ja antaa sille normaalikiihtyvyyden 
b)
Newtonin II-lain mukaan 
y-suunnassa:  eli
eli
Paino ja langan jännitysvoima pusyusiinyaonen kompenentti ovat yhtä suuret ja vastakkaissuuntaiset, joten ne kumoavat toisensa.
x-suunnassa: 
Ratkaistaan  suorakulmaisen kolmion trigonometrian avulla.
suorakulmaisen kolmion trigonometrian avulla.
Ratkaistaan kulma α
Suunnat huomioiden saadaan
2-10
Laskijan liikeyhtälö on  eli
eli 
Kun suunta ylös on positiivinen, skalaariyhtälöstä Kpl.1
Esimerkki

















 b)
b)


















a) Muunna asteiksi 1,2 rad
b) Muunna radiaaneiksi 185°
a)
b)
1-1
1-2
a)
b)
1-5
1-6
a) Kiertokulma on )
Kiertokulma on ympyrän kaaren pituuden ja säteen suhde eli 
1-7
a)
b)
1-10
a)
b)
1-12
a)
Kyllä, koska niiden liikeistä on mahdollista saada lireaarisen kuvaajan.
b)
A, koska sen kuvaajan kuvaaja on jyrkempi (n. 13 rad/s)
c)