Kpl.2
2-3
a) Gravitaati voima
b) Istuimen ketjujen jännitysvoima, kitka
c) Lepokitka
2-4
a) Tosi
b) Epätosi
c) Epätosi
2-5
V: A:ssa on suurempi



 eli
eli  . Koska sekä kitka että normaalikiihtyvyys suuntautuvat kohti ympyräradan keskipistettä, yhtälöstä
. Koska sekä kitka että normaalikiihtyvyys suuntautuvat kohti ympyräradan keskipistettä, yhtälöstä  eli
eli  saadaan kitkakertoimeksi
saadaan kitkakertoimeksi
%5E2%7D%7B22m%5Ccdot9%7B%2C%7D81%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%7D%3D0%7B%2C%7D1158372718)
2-6
a)
Koska ilmavastus on pieni, autoon vaikuttava kokonaisvoima on  . Koska pinta on vaakasuora, pinnan tukivoima
. Koska pinta on vaakasuora, pinnan tukivoima  ja autoon kohdistuva paino
ja autoon kohdistuva paino ovat yhtä suuret ja vastakkaisuunatiset, joten ne kumoavat toisensa. Kitka
ovat yhtä suuret ja vastakkaisuunatiset, joten ne kumoavat toisensa. Kitka  pitää auton ympyräradalla. Newtonin II lain mukaan jään pinnan suunnassa on
pitää auton ympyräradalla. Newtonin II lain mukaan jään pinnan suunnassa on
b)
Pysyy, koska saattu kitka on suurempi kuin 1,4kN
2-9
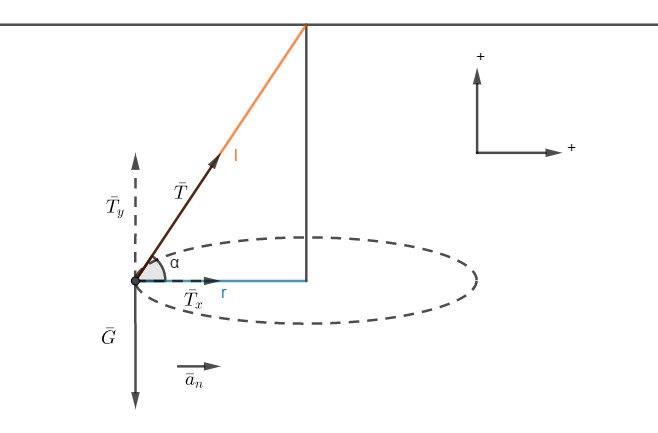
a)
Oletetaan ilmanvastus pieneksi.
Koneeseen vaikuttavat voimat ovat langan jännitysvoima  ja paino
ja paino 
Langan jännitysvoiman vaakasuuntaan komponentti itä koneen ympyräradalla ja antaa sille normaalikiihtyvyyden 
b)
Newtonin II-lain mukaan 
y-suunnassa:  eli
eli
Paino ja langan jännitysvoima pusyusiinyaonen kompenentti ovat yhtä suuret ja vastakkaissuuntaiset, joten ne kumoavat toisensa.
x-suunnassa: 
Ratkaistaan  suorakulmaisen kolmion trigonometrian avulla.
suorakulmaisen kolmion trigonometrian avulla.
Ratkaistaan kulma α
Suunnat huomioiden saadaan
2-10
Laskijan liikeyhtälö on  eli
eli 
Kun suunta ylös on positiivinen, skalaariyhtälöstä