FY4S
Kpl.16
16-1
a) on
b) on
c) ei
d) ei
e) on
16-4






%5Coverline%7Bu%7D) Sovitaan autojen alkuperäinen liikesuunta positiiviseksi, saadaan lause:
Sovitaan autojen alkuperäinen liikesuunta positiiviseksi, saadaan lause:
%3D93%7B%2C%7D591...%5Capprox94%5C%20%5Cfrac%7Bkm%7D%7Bh%7D)
16-5





u)


%3Dm_2u)

16-8
a) Kappale A liikkuu alussa tasaisella nopeudella, sitten hetkessä 0,50s se törmää kappaleen B, sen jälkeen kappale A:n nopeus hidastuu, ja kappale alkaa siitä liikkumaan.
b)









%3Dm_2u_2)

16-9
16-10







Sunnat huomioiden saadaan



%5E2%7D%7B9%7B%2C%7D81%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%7D%5Capprox0%7B%2C%7D13m)
a) on
b) on
c) ei
d) ei
e) on
16-4
Koska autojen muodot muuttuvat, törmmäys on kimmoton, joten säilymislaki olisi tässä muodossa:
16-5
16-8
a) Kappale A liikkuu alussa tasaisella nopeudella, sitten hetkessä 0,50s se törmää kappaleen B, sen jälkeen kappale A:n nopeus hidastuu, ja kappale alkaa siitä liikkumaan.
b)
16-9
16-10
Törmäyksen seurauksena paikallaan oleva vaunu b lähtee liikkumaan tasoa ylöspäin. aunun b saama liike.energia muuttuu potentiaalienergiaksi.
Sovitaan potentiaalienergian nolla tasoksi tason alaosa ja positiiviseksi liikesunnaksi vaunun a alkuperäinen liikesuunta (oikealle).
Liikemäärä säily, joten
Sunnat huomioiden saadaan
Ratkaistaan vaunun b nopeus
Vierimisvastus on merkityksetön, jote energia säilyy



Kpl.15
15-1
a)
 b)
b)






15-2
Impulssien suuruudet saadaan kuvaajista graafisella integroinnilla eli arvioimalla kuvaajien ja t-akselin väliin jäävän pinnan fysikaalinen pintaala. Yhden ruudun fysikaalinen pinta-ala on 1 s · 1 N = 1 Ns. Molemmissa tapauksissa impulssin suuruudeksi saadaan noin 6 Ns. Impulssit eroavat siten, että a-tapauksessa vaikuttava voima on suurempi kuin btapauksessa, ja a-tapauksessa voiman vaikutusaika on pidempi kuin btapauksessa. Vaikka impulssit ovat yhtä suuret, voiman vaikutus ei aina ole samanlainen. Suurempi voima saattaa esimerkiksi rikkoa rakenteita, mutta pienempi voima ei, vaikka voimien impulssit olisivat yhtä suuret.
15-4
Mailan palloon kohdistavan voiman impulssi on yhtä suuri kuin pallon liikemäärän muutos:

Sovitaan voiman suunta positiiviseksi, jolloin pallon suunta ennen mailaan osumista on negatiivinen. Saadaan skalaariyhtälö) .
.
Maila vaikuttaa palloon voimalla

%3Dm%5Cleft(v_2%2Bv_1%5Cright))
%7D%7B%5CDelta%20t%7D%3D%5Cfrac%7B0%7B%2C%7D057kg%5Ccdot%5Cleft(30%5C%20%5Cfrac%7Bm%7D%7Bs%7D%2B20%5C%20%5Cfrac%7Bm%7D%7Bs%7D%5Cright)%7D%7B0%7B%2C%7D020s%7D%3D142%7B%2C%7D5N%5Capprox140N) Keskimääräisen voiman suuruus on 140 N ja suunta on vastakkainen pallon alkuperäiseen liikesuuntaan nähden.
Keskimääräisen voiman suuruus on 140 N ja suunta on vastakkainen pallon alkuperäiseen liikesuuntaan nähden.
15-5


%3D2%7B%2C%7D475Ns)


15-7







%7D%7B0%7B%2C%7D004s%7D%3D975N%5Capprox980N%3D0%7B%2C%7D98kN)
15-8
a)
15-2
Impulssien suuruudet saadaan kuvaajista graafisella integroinnilla eli arvioimalla kuvaajien ja t-akselin väliin jäävän pinnan fysikaalinen pintaala. Yhden ruudun fysikaalinen pinta-ala on 1 s · 1 N = 1 Ns. Molemmissa tapauksissa impulssin suuruudeksi saadaan noin 6 Ns. Impulssit eroavat siten, että a-tapauksessa vaikuttava voima on suurempi kuin btapauksessa, ja a-tapauksessa voiman vaikutusaika on pidempi kuin btapauksessa. Vaikka impulssit ovat yhtä suuret, voiman vaikutus ei aina ole samanlainen. Suurempi voima saattaa esimerkiksi rikkoa rakenteita, mutta pienempi voima ei, vaikka voimien impulssit olisivat yhtä suuret.
15-4
Mailan palloon kohdistavan voiman impulssi on yhtä suuri kuin pallon liikemäärän muutos:
Sovitaan voiman suunta positiiviseksi, jolloin pallon suunta ennen mailaan osumista on negatiivinen. Saadaan skalaariyhtälö
Maila vaikuttaa palloon voimalla
15-5
15-7
15-8
Impulssiperiaatteen mukaan pallon törmäyksessä vaikuttavan voiman impulssi on yhttä suuri kuin sen liikemäärän muuts eli
Siis
Ratkaistaan eli pallon nopeus sen osuessa energiaperiaatten aulla.
eli pallon nopeus sen osuessa energiaperiaatten aulla.
Valitaan nollatasoksi lattian taso. Tällöin pallon potentiaalienergia muuttuu pudotuksessa liike-energiaksi eli
15-9
a)





)


Kpl.14
14-2




![v=\sqrt[]{2gh}=\sqrt[]{2\cdot9{,}81\ \frac{m}{s^2}\cdot25m}=22{,}147...\approx22\ \frac{m}{s}](https://math-demo.abitti.fi/math.svg?latex=v%3D%5Csqrt%5B%5D%7B2gh%7D%3D%5Csqrt%5B%5D%7B2%5Ccdot9%7B%2C%7D81%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%5Ccdot25m%7D%3D22%7B%2C%7D147...%5Capprox22%5C%20%5Cfrac%7Bm%7D%7Bs%7D)
14-4
a)



b)




14-5
a)










![v_l=\sqrt[]{\frac{mv_a^2+2\left(W+mgh_a\right)}{m}}=45{,}92009...\approx46\ \frac{km}{h}](https://math-demo.abitti.fi/math.svg?latex=v_l%3D%5Csqrt%5B%5D%7B%5Cfrac%7Bmv_a%5E2%2B2%5Cleft(W%2Bmgh_a%5Cright)%7D%7Bm%7D%7D%3D45%7B%2C%7D92009...%5Capprox46%5C%20%5Cfrac%7Bkm%7D%7Bh%7D)
b)
14-6








%5E2-71kg%5Ccdot9%7B%2C%7D81%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%5Ccdot66m%3D-180287%7B%2C%7D10599J%5Capprox-18000J%3D-18kJ)
14-7






Valitaan ,että mäen alla on potentiaalienergian nollataso eli



![v_l=\sqrt[]{\frac{2Fs+m\left(v_a^2+2gh_a\right)}{m}}](https://math-demo.abitti.fi/math.svg?latex=v_l%3D%5Csqrt%5B%5D%7B%5Cfrac%7B2Fs%2Bm%5Cleft(v_a%5E2%2B2gh_a%5Cright)%7D%7Bm%7D%7D)
![v_l=\sqrt[]{\frac{2\cdot\left(-55N\right)\cdot35m+73kg\left(\left(2{,}5\ \frac{m}{s}\right)^2+2\cdot9{,}81\ \frac{m}{s^2}\cdot8{,}0m\right)}{73kg}}=10{,}510484\ \frac{m}{s}\approx11\ \frac{m}{s}](https://math-demo.abitti.fi/math.svg?latex=v_l%3D%5Csqrt%5B%5D%7B%5Cfrac%7B2%5Ccdot%5Cleft(-55N%5Cright)%5Ccdot35m%2B73kg%5Cleft(%5Cleft(2%7B%2C%7D5%5C%20%5Cfrac%7Bm%7D%7Bs%7D%5Cright)%5E2%2B2%5Ccdot9%7B%2C%7D81%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%5Ccdot8%7B%2C%7D0m%5Cright)%7D%7B73kg%7D%7D%3D10%7B%2C%7D510484%5C%20%5Cfrac%7Bm%7D%7Bs%7D%5Capprox11%5C%20%5Cfrac%7Bm%7D%7Bs%7D)
14-8









14-9
a)









b)












%5E%7B%5E2%7D%7D%7B2%5Ccdot0%7B%2C%7D77%7B%2C%7D9%7B%2C%7D81%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%7D%5Capprox1%7B%2C%7D7m)
14-4
a)
b)
14-5
a)
b)
14-6
14-7
Valitaan ,että mäen alla on potentiaalienergian nollataso eli
Liikettä vastustava voima muuttaa mekaanista energiaa lumen, lumilaudan ja ilman sisäenergiaksi.
Mekaniikan energianperiaatteen mukaan
14-8
14-9
a)
b)
Kpl.13
13-1
a) Väärin. Potentiaalienergian nollatason voi valita tilanteen mukaan mille korkeudelle tahansa.
b) Oikein.
c) Oikein.
d) Oikein.
e) Oikein.
f) Väärin. Kun kappaleeseen vaikuttaa kitka, kappaleen mekaaninen energia ei säily vaan pienenee. Kitka on siis ei-konservatiivinen voima.
13-2
a)

b)
 13-5
13-5
13-6

a) Väärin. Potentiaalienergian nollatason voi valita tilanteen mukaan mille korkeudelle tahansa.
b) Oikein.
c) Oikein.
d) Oikein.
e) Oikein.
f) Väärin. Kun kappaleeseen vaikuttaa kitka, kappaleen mekaaninen energia ei säily vaan pienenee. Kitka on siis ei-konservatiivinen voima.
13-2
a)
b)
13-6
Kpl.12
12-1
a)
%5E2%5Cfrac%7Bm%7D%7Bs%7D%3D83J)
b)
%5E2%5C%20%5Cfrac%7Bm%7D%7BS%7D%3D4243%7B%2C%7D82...%5Capprox4%7B%2C%7D2kJ)
12-2
%5E2%5C%20%5Cfrac%7Bm%7D%7Bs%7D%3D390625J)


![v_{rekka}=\sqrt[]{\frac{E_{k{,}auto}}{\frac{1}{2}m_{rekka}}}](https://math-demo.abitti.fi/math.svg?latex=v_%7Brekka%7D%3D%5Csqrt%5B%5D%7B%5Cfrac%7BE_%7Bk%7B%2C%7Dauto%7D%7D%7B%5Cfrac%7B1%7D%7B2%7Dm_%7Brekka%7D%7D%7D)

![x=\sqrt[]{\frac{390625J}{\frac{1}{2}\cdot40000kg}}=4{,}4194...\ \frac{m}{s}=15{,}909...\approx16\frac{km}{h}](https://math-demo.abitti.fi/math.svg?latex=x%3D%5Csqrt%5B%5D%7B%5Cfrac%7B390625J%7D%7B%5Cfrac%7B1%7D%7B2%7D%5Ccdot40000kg%7D%7D%3D4%7B%2C%7D4194...%5C%20%5Cfrac%7Bm%7D%7Bs%7D%3D15%7B%2C%7D909...%5Capprox16%5Cfrac%7Bkm%7D%7Bh%7D)
12-5
12-9
a)
b)
12-2
12-5
12-9
Kpl.11
11-3
a)

b)

11-4
a)

b)
26kJ
11-5
11-7
11-10


 eli
eli . Valitaan suunta ylös positiivisekski, jolloin
. Valitaan suunta ylös positiivisekski, jolloin
 eli
eli .Nostava voima on koneen painon suuruinen, joten työ on
.Nostava voima on koneen painon suuruinen, joten työ on


11-14
a)
b)
11-4
a)
b)
26kJ
11-5
11-7
11-10
a)
Oletetaan, että lentokone nousee vakionopeudella, jolloin
b)
11-14
Kpl.10
10-3
a) Painonnostokilpailussa painoja on helpompi nostaa, jos painot ovat yhtä suuret ja tangon eri päissä. Painopiste on tangon geometrisessä keskipisteessä. Painonnostaja pyrkii asettamaan kätensä yhtä kauas tangon painopisteestä (geometrisestä keskipisteestä).
b) Painonnostossa käytetään leveää otetta, jolloin tanko on mahdollisimman helppo pitää tasapainossa. Raskaat levyt tangon päissä aiheuttavat suuren momentin tankoon. Jos kädet olisivat lähekkäin, pienikin ero käsien ja tangon keskipisteen välisissä etäisyyksissä aiheuttaisi suuren eron vasempaan ja oikeaan käteen kohdistuvissa voimissa. Samoin pienikin tangon kiertoliike tangon keskipisteen ympäri noston aikana olisi vaikea pysäyttää, nostaja menettäisi helposti tasapainonsa sivusuunnassa.
10-4
Joidenkin kukkien, esimerkiksi tulppaanien, varsi kasvaa nopeasti maljakossa. Samalla maljakon pohjalla oleva vesi vähenee sen noustessa varteen. Kukat voivat taipua kasvaessaan kauas reunan yli, ja kukkaasetelman painopiste muuttuu. Maljakon, veden ja kukkien yhteinen painopiste voi siirtyä maljakon kapean pohjan tukipinnan ulkopuolelle, varsinkin jos kukat taipuvat samaan suuntaan. Näin maljakko voi kaatua itsestään.
10-7
Tasapaksuun hirteen kohdistuva paino vaikuttaa hirren painopisteeseen eli keskipisteeseen. Hirren tasapainoehto pystysuunnassa on eli
eli  . Kun suunta ylös on positiivinen, saadaan skalaariyhtälö
. Kun suunta ylös on positiivinen, saadaan skalaariyhtälö  .
.
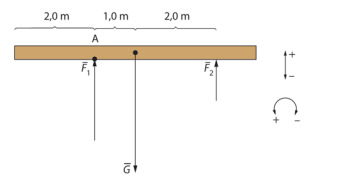
Vasemmanpuoleisen tukivoiman vaikutuskohta on A. Valitaan kohta A momenttiakseliksi. Kun kiertosuunta vastapäivään on positiivinen, akselin A suhteen momenttiyhtälö on
vaikutuskohta on A. Valitaan kohta A momenttiakseliksi. Kun kiertosuunta vastapäivään on positiivinen, akselin A suhteen momenttiyhtälö on 
Tukivoiman suuruus on
suuruus on

Tukivoman suuruus saadaan yhtälöstä
suuruus saadaan yhtälöstä  , joten
, joten 
Voimat ovat 460N ja 920N
10-9



 : Väijerin jännitysvoima
: Väijerin jännitysvoima
 : Painovoima
: Painovoima
 : Saranan tukivoima
: Saranan tukivoima



















![F=\sqrt[]{F_x^2+F_y^2}=\sqrt[]{382{,}59^2+765{,}18^2}=855{,}49...\approx860N](https://math-demo.abitti.fi/math.svg?latex=F%3D%5Csqrt%5B%5D%7BF_x%5E2%2BF_y%5E2%7D%3D%5Csqrt%5B%5D%7B382%7B%2C%7D59%5E2%2B765%7B%2C%7D18%5E2%7D%3D855%7B%2C%7D49...%5Capprox860N)


10-11

Lankun alapäässä vaikuttavat lattian tukivoima ja kitka
ja kitka  . Yläpäässä lankkuun kohdistuu seinän tukivoima
. Yläpäässä lankkuun kohdistuu seinän tukivoima ja koska seinä oletettiin liukkaaksi, kitka
ja koska seinä oletettiin liukkaaksi, kitka . Lankun painopisteessä vaikuttaa lankkuun kohdistuva paino
. Lankun painopisteessä vaikuttaa lankkuun kohdistuva paino 
Tasapainoehto vaakasuunnassa on Newtonin II lain perusteella eli
eli  . Kun suunta oikealle on positiivinen, skalaariyhtälöstä
. Kun suunta oikealle on positiivinen, skalaariyhtälöstä  saadaan
saadaan 
Asetetaan momenttiakseli pisteeseen A. Kun kiertosuunta vastapäivään on positiivinen, tasapainotilanteessa momenttien summa akselin A suhteen on eli
eli  .Koska
.Koska 
momenttiehto saadaan muotoon
saadaan muotoon  eli
eli  ,
,
josta saadaan .
.
Toisaakta suorakulmaisen kolmion trigonometrian perusteella on
 , joten yhtälöstä
, joten yhtälöstä

saadaan kulma
a) Painonnostokilpailussa painoja on helpompi nostaa, jos painot ovat yhtä suuret ja tangon eri päissä. Painopiste on tangon geometrisessä keskipisteessä. Painonnostaja pyrkii asettamaan kätensä yhtä kauas tangon painopisteestä (geometrisestä keskipisteestä).
b) Painonnostossa käytetään leveää otetta, jolloin tanko on mahdollisimman helppo pitää tasapainossa. Raskaat levyt tangon päissä aiheuttavat suuren momentin tankoon. Jos kädet olisivat lähekkäin, pienikin ero käsien ja tangon keskipisteen välisissä etäisyyksissä aiheuttaisi suuren eron vasempaan ja oikeaan käteen kohdistuvissa voimissa. Samoin pienikin tangon kiertoliike tangon keskipisteen ympäri noston aikana olisi vaikea pysäyttää, nostaja menettäisi helposti tasapainonsa sivusuunnassa.
10-4
Joidenkin kukkien, esimerkiksi tulppaanien, varsi kasvaa nopeasti maljakossa. Samalla maljakon pohjalla oleva vesi vähenee sen noustessa varteen. Kukat voivat taipua kasvaessaan kauas reunan yli, ja kukkaasetelman painopiste muuttuu. Maljakon, veden ja kukkien yhteinen painopiste voi siirtyä maljakon kapean pohjan tukipinnan ulkopuolelle, varsinkin jos kukat taipuvat samaan suuntaan. Näin maljakko voi kaatua itsestään.
10-7
Tasapaksuun hirteen kohdistuva paino vaikuttaa hirren painopisteeseen eli keskipisteeseen. Hirren tasapainoehto pystysuunnassa on

Vasemmanpuoleisen tukivoiman
Tukivoiman
Tukivoman
Voimat ovat 460N ja 920N
10-9
Tasapainoehto etenemisen suhteen x-suunnassa
Tasapainoehto etenemisen suhteen y-suunnassa
Tasapainoehto pyörimisen suhteen
a)
b)
Voiman suunta
10-11

Lankun alapäässä vaikuttavat lattian tukivoima
Tasapainoehto etenemisen suhteen pystysuunnassa on Newtonin II lain perusteella  eli
eli  . Kun suunta ylös on positiivinen, skalaariyhtälöstä
. Kun suunta ylös on positiivinen, skalaariyhtälöstä  saadaan
saadaan  .
.
Tasapainoehto vaakasuunnassa on Newtonin II lain perusteella
Asetetaan momenttiakseli pisteeseen A. Kun kiertosuunta vastapäivään on positiivinen, tasapainotilanteessa momenttien summa akselin A suhteen on
momenttiehto
josta saadaan
Toisaakta suorakulmaisen kolmion trigonometrian perusteella on
saadaan kulma
Kpl.9
9-2
Jos soudan oikean käden puoleisella airolla voimakkaammin kuin vasemman käden puoleisella airolla, vesi kohdistaa oikean käden puoleiseen airoon suuremman voiman kuin vasemman käden puoleiseen airoon. Tällöin suuremman voiman aiheuttama vääntömomentti on suurempi ja vene kääntyy vasemman käden suuntaan eli kulkusuunnassa oikealle.
9-4
Tarvittava voima on pienin, kun voima on kohtisuorassa voiman vartta vastaan. Voiman momentti on M = Fr, joten pienimmän voiman suuruus on

9-7
a)
Kun momentin kiertosuunta vastapäivään on positiivinen, voiman F1 momentti akselin A suhteen on

b)
Kun kulma α = 90°, voimien momenttien summa on

Jos kulma α = 50°, voiman 2 F vartta vastaan kohtisuora komponentti on
 Momenttien summa akselin A suhteen on
Momenttien summa akselin A suhteen on

Momentti on 1,5Nm myötäpäivään.
9-8
Koska voiman momentti on kääntäen verrannollinen voiman vaikutussuoran etäisyyteen kiertoakselista, lisätään taulukkoon arvot 1/r.
Viedään arvot 1/r,F mittausohjelmaan.

Mittausohjelman perusteella voiman momentti on 5,5 Nm. Momentin kiertosuunta on vastapäivään.
9-10
Valitaan kiertosuunta vastapäivään positiiviseksi. Tukki irtoaa tueltaan, jos nostavan voiman momentti positiiviseen kiertosuuntaan on suurempi kuin painon momentti negatiiviseen kiertosuuntaan. Tällöin tukki joutuu pyörimisliikkeeseen akselin A ympäri.
Painon momentti negatiiviseen kiertosuuntaan on

Kahvasta nostettaessa voiman momentin pitää olla positiiviseen kiertosuuntaan suurempi kuin 676,89 Nm. Rajatapauksessa, jolloin tukki on irtoamassa alustastaan, voiman momentti on
 , eli
, eli 
Näin ollen eri kahvoista nostettaessa tarvittavan voiman suuruus on suurempi kuin




Osoittajan tarkkuus on kaksi merkitsevää numeroa. Siksi vastaustenkin tarkkuus on kaksi merkitsevää numeroa.
Jos soudan oikean käden puoleisella airolla voimakkaammin kuin vasemman käden puoleisella airolla, vesi kohdistaa oikean käden puoleiseen airoon suuremman voiman kuin vasemman käden puoleiseen airoon. Tällöin suuremman voiman aiheuttama vääntömomentti on suurempi ja vene kääntyy vasemman käden suuntaan eli kulkusuunnassa oikealle.
9-4
Tarvittava voima on pienin, kun voima on kohtisuorassa voiman vartta vastaan. Voiman momentti on M = Fr, joten pienimmän voiman suuruus on
9-7
a)
Kun momentin kiertosuunta vastapäivään on positiivinen, voiman F1 momentti akselin A suhteen on
b)
Kun kulma α = 90°, voimien momenttien summa on
Jos kulma α = 50°, voiman 2 F vartta vastaan kohtisuora komponentti on
Momentti on 1,5Nm myötäpäivään.
9-8
Koska voiman momentti on kääntäen verrannollinen voiman vaikutussuoran etäisyyteen kiertoakselista, lisätään taulukkoon arvot 1/r.
| r(m) | 0,15 | 0,30 | 0,45 | 0,60 | 0,75 |
| 1/r(1/m) | 6,67 | 3,33 | 2,22 | 1,67 | 1,33 |
| F(N) | 36,5 | 17,8 | 12,0 | 8,8 | 7,3 |
Viedään arvot 1/r,F mittausohjelmaan.

Mittausohjelman perusteella voiman momentti on 5,5 Nm. Momentin kiertosuunta on vastapäivään.
9-10
Valitaan kiertosuunta vastapäivään positiiviseksi. Tukki irtoaa tueltaan, jos nostavan voiman momentti positiiviseen kiertosuuntaan on suurempi kuin painon momentti negatiiviseen kiertosuuntaan. Tällöin tukki joutuu pyörimisliikkeeseen akselin A ympäri.
Painon momentti negatiiviseen kiertosuuntaan on
Kahvasta nostettaessa voiman momentin pitää olla positiiviseen kiertosuuntaan suurempi kuin 676,89 Nm. Rajatapauksessa, jolloin tukki on irtoamassa alustastaan, voiman momentti on
Näin ollen eri kahvoista nostettaessa tarvittavan voiman suuruus on suurempi kuin
Osoittajan tarkkuus on kaksi merkitsevää numeroa. Siksi vastaustenkin tarkkuus on kaksi merkitsevää numeroa.
Kpl.8
8-2
 b)
b)
 8-3
8-3
%3D2636%7B%2C%7D343...%5Capprox2%7B%2C%7D6kN)
%3D4265%7B%2C%7D544...%5Capprox4%7B%2C%7D3kN)

8-4



8-12



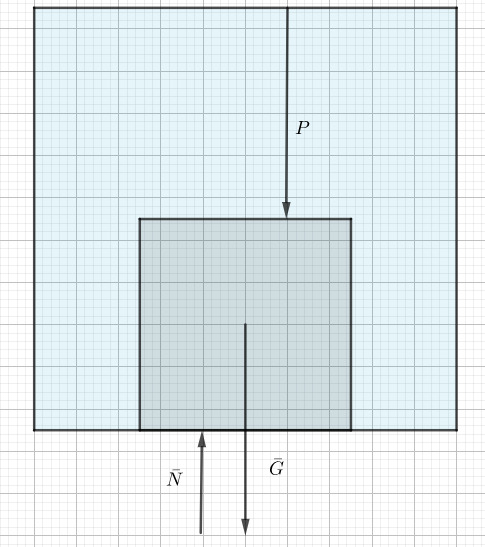
 Rajatapauksessa palloon kohdistuva noste on yhtä suuri kuin palloon kohdistuva kokonaispaino
Rajatapauksessa palloon kohdistuva noste on yhtä suuri kuin palloon kohdistuva kokonaispaino




-m_%7Bpallo%7D%3D160%5C%20m%5E3%5Cleft(1%7B%2C%7D3%5C%20%5Cfrac%7Bkg%7D%7Bm%5E3%7D-0%7B%2C%7D85%5C%20%5Cfrac%7Bkm%7D%7Bm%5E3%7D%5Cright)-23%5C%20kg%3D49kg)
8-13
a)
Epäily rautalaivojen kellumisesta johtui siitä, että raudan tiheys oli suurempi kuin veden. Rautalaivan pysyminen pinnalla johtuu veden nosteesta. Kelluva laiva on ontto, eli valtaosa laivan tilavuudesta on ilmaa. Laivan kohdistuva veden noste on yhtä suuri kuin laivan syrjäyttämään vesimäärän kohdistuva paino.
b)
Pelastusliivit valmistetaan vedenpitävästä, kevyestä ja kelluvasta materiaalista. Pelastusliivien varassa igminen kelluu, vaikak uimiseen tai veden pinnalla pysymiseen tarvittavat voimat vedessä loppuisivat. Varsinaisten pelastusliivien (ei uimaliivien) etupuolella on suuret kellukkeet, jotka kääntävät veden varaan joutuneen tajuttoman henkilön selälleen, jollin pää pysyy veden yläpuolella.
8-14
Alussa palloa on helppo, koska vedestä palloon kohdistuva noste on pieni. Mitä syvemmälle painetaan palloa, sitä suurempi noste on. Nosteen suuruus riippuu vedenpinnan alapuolella olevan pallon osan tilavuudesta.
a)

a)
Yläpinta:
Alapinta:
b)
8-4
a)
b)
Sama kuin vedessä eli 1,2 kg
c)
d)
Kivi pysyy paikallaan, kun sitä tuetaan ylöspäi suuntautuvalla voimalla, jonka suuruus on:
8-12
Tasapainoehto on  eli
eli . Valitaan suunta alsa positiiviseksi.
. Valitaan suunta alsa positiiviseksi.
8-13
a)
Epäily rautalaivojen kellumisesta johtui siitä, että raudan tiheys oli suurempi kuin veden. Rautalaivan pysyminen pinnalla johtuu veden nosteesta. Kelluva laiva on ontto, eli valtaosa laivan tilavuudesta on ilmaa. Laivan kohdistuva veden noste on yhtä suuri kuin laivan syrjäyttämään vesimäärän kohdistuva paino.
b)
Pelastusliivit valmistetaan vedenpitävästä, kevyestä ja kelluvasta materiaalista. Pelastusliivien varassa igminen kelluu, vaikak uimiseen tai veden pinnalla pysymiseen tarvittavat voimat vedessä loppuisivat. Varsinaisten pelastusliivien (ei uimaliivien) etupuolella on suuret kellukkeet, jotka kääntävät veden varaan joutuneen tajuttoman henkilön selälleen, jollin pää pysyy veden yläpuolella.
8-14
Alussa palloa on helppo, koska vedestä palloon kohdistuva noste on pieni. Mitä syvemmälle painetaan palloa, sitä suurempi noste on. Nosteen suuruus riippuu vedenpinnan alapuolella olevan pallon osan tilavuudesta.
Kpl.7
Kpl.6
Kpl.5
Kokonaisvoima on 
Kappale ei liiku pystysuunnassa, joten
Sklaraaariyhtälö on  eli N=G
eli N=G
skalaarimuodossa
c)
Newtonin II lain mukaan 
b-kohdan nojalla
5-5
a)
Maan vetovoima
Tukivoima (ilmavastus)
b)

a) 720 N
5-9
5-10
a)

Koska venymättömän langan jännitysvoima on langan molemmissa päissä yhtä suuri, on T1=T2. Kappaleilla on sama kiihtyvyyden suuruus, koska ne liikkuvat yhdessä: a1=a2.
Kappale m1: Newtonin II lain mukaan on
Kappae m2: Newtonin II lain mukaan on
Saadaan yhtälöpari:
Kerrotaan alempi yhtälö luvulla -1 ja lasketaan yhtälöt yhteen (eli vähennetään puolittain ylemmästä yhtälöstä alempi). Näin saadaan yhtälö g(m2-m1)=(m2+m1)a, josta kiihtyvyys on.
Koska kiihtyvyyden arvo on positiivinen, kappaleen 1 kiihtyvyys on ylös ja kappaleen 2 vastaavasti alas kuten tilanteesta on muutenkin pääteltävissä. Langan jännitysvoiman suuruus on
b)
Kappale m2 törmää lattiaan nopeudella
Kpl.4
4-1
a)
Sauvamagneetin ja Maan välillä vallitsee gravitaatiovuorovaikutus. Maan ja magneetin välillä on magneettinen vuorovaikutus. Kosketusvuorovaikutus on langan ja magneetin välillä. Magneetin ja ilman välillä on kosketusvuorovaikutus.
b)
Gravitaatiovuorovaikutus: kärryt ja Maa. Kosketusvuorovaikutus: lattia ja kärryt. Kosketusvuorovaikutus: työntäjä ja kärry. Kosketusvuorovaikutus: lattia ja kärryt. Kosketusvuorovaikutus: kärryt ja ilma.
c)
Gravitaatiovuorovaikutus: Maa ja pallo. Sähköinen vuorovaikutus: pallot keskenään. Kosketusvuorovaikutus: lanka ja pallo. Kosketusvuorovaikutus: pallo ja ilma.
4-4
a)
150N
b)
150N
c)
Kestää
4-5
a)
F1: Vetävä voima
F2: Ilmavastus
F3: Tukivoima
F4: Gravitaatiovoima/ maapellon vetovoima
F5: Kitka
b)
F1: Ilmavastus
F2: Maapallon vetovoima
c)
F1: Vetävä voima
F2: Maapallon vetovoima
F3: Tukivoima
4-8
a)
Jään ja ilman kanssa ja etävuorovaikutuksessa maan kanssa maapallon vetovoimalla.
b)
Kiekkoa kiihtyvä lyönnin voima
Maapallon vetovoima
Kitka
Ilmavastus
Tukivoima
c)

d)
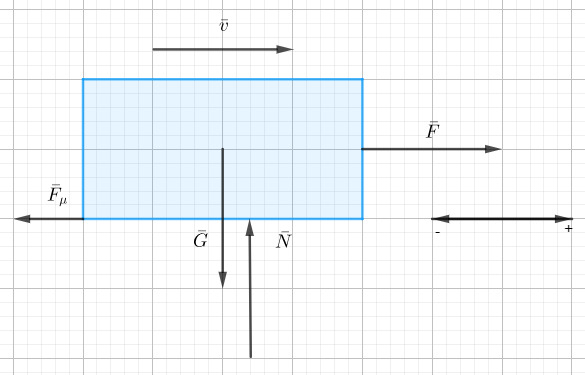
Painon G vastavoima on voima, jolla kiekko vetää Maata. Tukivoiman N vastavoima on voima, jolla kiekko painaa jäätä. Kitkan Fµ vastavoima on voima, jolla kiekko vaikuttaa jään pintaan. Ilmanvastuksen Fi vastavoima on voima, jolla kiekko vaikuttaa ilmaan.
4-9
Havaitsemissasi ilmiöissä kyse ei ole voimista vaan siitä, että massasi vastustaa liikkeesi muuttumista, kun bussin liike muuttuu. Kaikki havaitsemasi ilmiöt johtuvat massan hitaudesta.
4-10
a) Voimat F3 ja F4 eivät ole voima ja vastavoima, koska ne vaikuttavat samaan kappaleeseen (lamppuun).
b) Voiman F2 vastavoima on F3.
c) Voiman F6 vastavoima on voima, jolla lamppu vetää Maata.
d) Voima F5 on tukivoima, jolla naru estää lampun putoamisen. Voima F6 on voima, jolla Maa vetää lamppua.
4-12

a)
Sauvamagneetin ja Maan välillä vallitsee gravitaatiovuorovaikutus. Maan ja magneetin välillä on magneettinen vuorovaikutus. Kosketusvuorovaikutus on langan ja magneetin välillä. Magneetin ja ilman välillä on kosketusvuorovaikutus.
b)
Gravitaatiovuorovaikutus: kärryt ja Maa. Kosketusvuorovaikutus: lattia ja kärryt. Kosketusvuorovaikutus: työntäjä ja kärry. Kosketusvuorovaikutus: lattia ja kärryt. Kosketusvuorovaikutus: kärryt ja ilma.
c)
Gravitaatiovuorovaikutus: Maa ja pallo. Sähköinen vuorovaikutus: pallot keskenään. Kosketusvuorovaikutus: lanka ja pallo. Kosketusvuorovaikutus: pallo ja ilma.
4-4
a)
150N
b)
150N
c)
Kestää
4-5
a)
F1: Vetävä voima
F2: Ilmavastus
F3: Tukivoima
F4: Gravitaatiovoima/ maapellon vetovoima
F5: Kitka
b)
F1: Ilmavastus
F2: Maapallon vetovoima
c)
F1: Vetävä voima
F2: Maapallon vetovoima
F3: Tukivoima
4-8
a)
Jään ja ilman kanssa ja etävuorovaikutuksessa maan kanssa maapallon vetovoimalla.
b)
Kiekkoa kiihtyvä lyönnin voima
Maapallon vetovoima
Kitka
Ilmavastus
Tukivoima
c)

d)
Painon G vastavoima on voima, jolla kiekko vetää Maata. Tukivoiman N vastavoima on voima, jolla kiekko painaa jäätä. Kitkan Fµ vastavoima on voima, jolla kiekko vaikuttaa jään pintaan. Ilmanvastuksen Fi vastavoima on voima, jolla kiekko vaikuttaa ilmaan.
4-9
Havaitsemissasi ilmiöissä kyse ei ole voimista vaan siitä, että massasi vastustaa liikkeesi muuttumista, kun bussin liike muuttuu. Kaikki havaitsemasi ilmiöt johtuvat massan hitaudesta.
4-10
a) Voimat F3 ja F4 eivät ole voima ja vastavoima, koska ne vaikuttavat samaan kappaleeseen (lamppuun).
b) Voiman F2 vastavoima on F3.
c) Voiman F6 vastavoima on voima, jolla lamppu vetää Maata.
d) Voima F5 on tukivoima, jolla naru estää lampun putoamisen. Voima F6 on voima, jolla Maa vetää lamppua.
4-12

Kpl.3
Kpl.2
2-1
a)
Mopoauto kiihtyy aikavälillä 0-6s, sitten se alkoi liikkua vakionopeudella välillä 6-10s, lopuksi liike alkoi hidastua välillä 10-14s
b)
0,0s-6,0s: 2,0 m/s2
6,0s-10s: 0,0 m/s2
10s-14s: 3,0 m/s2
c)












%2B12%5C%20%5Cfrac%7Bm%7D%7Bs%7D%5Ccdot4s%2B%5Cfrac%7B1%7D%7B2%7D%5Ccdot0%7B%2C%7D0%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%5Ccdot4%5E2s)

%2B12%5C%20%5Cfrac%7Bm%7D%7Bs%7D%5Ccdot4s%2B%5Cfrac%7B1%7D%7B2%7D%5Ccdot%5Cleft(-3%7B%2C%7D0%5Cright)%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%5Ccdot4%5E2s)

2-2
a)

b)

c)








2-4
a)


2-6
a)




a)



c)


2-8
a)
Tilanteessa A jarrupoljinta painetaan ensin kevyesti, mutta painaminen kasvaa jarrutuksen edetessä. Tilanteessa B jarrupoljinta painetaan koko ajan samalla voimakkuudella. Tilanteessa C jarrupoljinta painetaan ensi hyvin voimakkaasti, mutta jarrutuksen edetessä poljinta löysätään hieman.
b) C
c) n.14 m
2-10
a)
Koska hissin kiihtyvyys on vakio, ja hissi lähtee levosta (v0 = 0 m/s), hissin keskinopeus ensimmäisen 5,0 m matkalla on , jossa v on tällä matkalla saavutettu loppunopeus ja myös hissin nopeus tasaisen liikkeen aikana.
, jossa v on tällä matkalla saavutettu loppunopeus ja myös hissin nopeus tasaisen liikkeen aikana.

Hissin loppunopeus ensimmäisen osuuden jälkeen eli hissin nopeus tasaisen liikkeen aikana on

b)
Hissi kulkee 19 kerrosväliä eli matkan 19 ∙ 2,8 m = 53,2 m. Jarrutusmatka on 53,2 m-5,0 m-44,0 m=4,2 m ja tähän kuluva aika

Koska hissi kulkee 44,0 m vakionopeudella, tähän kuluu aikaa
 Koko matkaan kuluva aika on
Koko matkaan kuluva aika on

2-13
a)




)
a)
Mopoauto kiihtyy aikavälillä 0-6s, sitten se alkoi liikkua vakionopeudella välillä 6-10s, lopuksi liike alkoi hidastua välillä 10-14s
b)
0,0s-6,0s: 2,0 m/s2
6,0s-10s: 0,0 m/s2
10s-14s: 3,0 m/s2
c)
2-2
a)

b)
c)
2-4
a)
b)

c)
c)
2-6
a)
b)

2-7a)
Suunta nopeuden sunnalle vastakkainen
b)
b)
c)
2-8
a)
Tilanteessa A jarrupoljinta painetaan ensin kevyesti, mutta painaminen kasvaa jarrutuksen edetessä. Tilanteessa B jarrupoljinta painetaan koko ajan samalla voimakkuudella. Tilanteessa C jarrupoljinta painetaan ensi hyvin voimakkaasti, mutta jarrutuksen edetessä poljinta löysätään hieman.
b) C
c) n.14 m
2-10
a)
Koska hissin kiihtyvyys on vakio, ja hissi lähtee levosta (v0 = 0 m/s), hissin keskinopeus ensimmäisen 5,0 m matkalla on
Hissin loppunopeus ensimmäisen osuuden jälkeen eli hissin nopeus tasaisen liikkeen aikana on
b)
Hissi kulkee 19 kerrosväliä eli matkan 19 ∙ 2,8 m = 53,2 m. Jarrutusmatka on 53,2 m-5,0 m-44,0 m=4,2 m ja tähän kuluva aika
Koska hissi kulkee 44,0 m vakionopeudella, tähän kuluu aikaa
2-13
a)
Alkunopeus: 
Vakiokiihtyvyys: 
Paikka alkuhetkellä:
Paikka hetkellä t
Ratkaistaan t yhtälöstä:
Laskinmen avulla saattiin ratkaisuksi -9,159s ja 1,012s, koska aika ei voi olla negatiivinen, sitä negatiivistä ratkaisua hylätään, ja lopuksi jää vastaukseski 1,012 s
Kpl.1
1-1
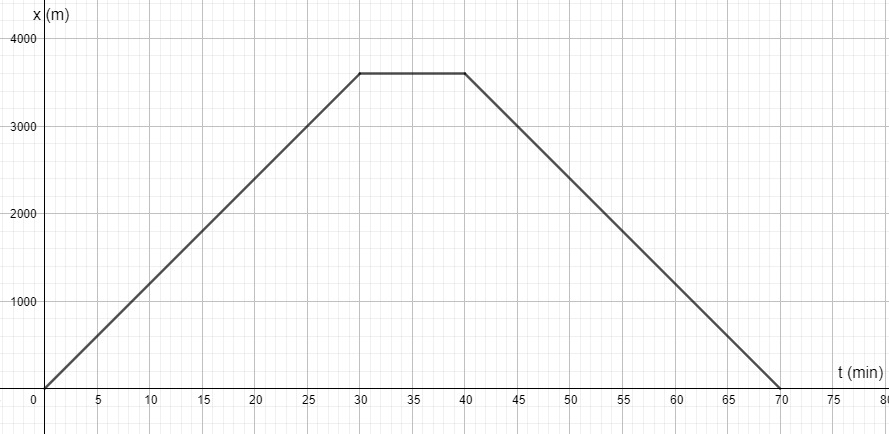
a) 10s-20s
b) 30s-40s
c) 10s-10s, 20s-30s, 40s-50s
d) 30s-40s
1-2
a) 2,0 m
b) 2,0 m/s
c) -6,0 m
d) 6,0 m/s, taaksepäin
e) -4,0 m/s
1-3
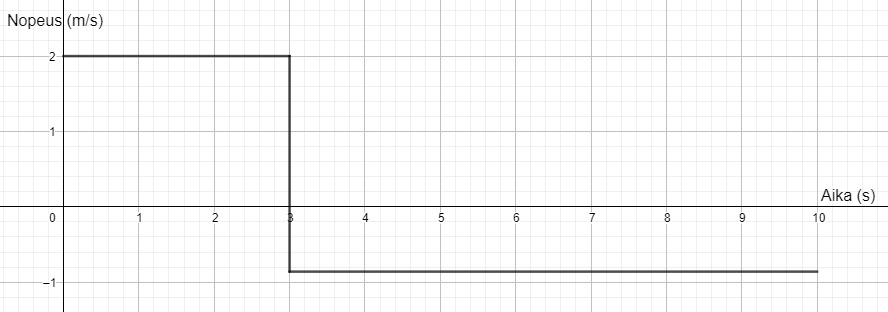
a) Nopeus kasvaa nopeasti välillä 0s-2s. sitten nopeus laskee ja kappale alkaa liikkumaan taaksepäin.
b) 12m
c)

 , taaksepäin
, taaksepäin
d)
1-4
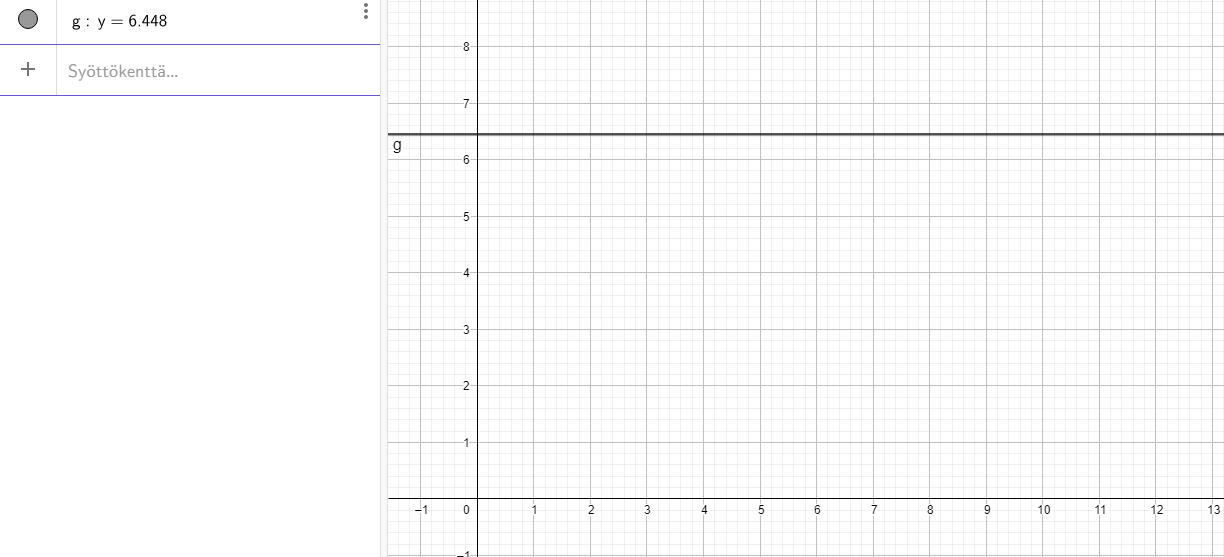
a)
Teoreettinen nopeus:
%3D10%5Ccdot0%7B%2C%7D1m%3D1%7B%2C%7D0m)
%3D21s-5s%3D16s)

Oikea nopeus:


b)
1-5

Kokkeen toiminnasta sanottiin, että ''Valonnopeuden mittauslaite lähettää valopulssiin ja vastaanottaa peilistä takaisin heijastuneen pulssin sekä rekisteröi pulssin lähdön ja paluun väliseen aikaeron. Kokeessa peilin etäisyyttä (s) mittalaitteesta muutettiin metrin välein ja mitattiin aikaerot (t), jolloin saatiin alla olevan taulukon mukaiset tulokset.''. Tämän mukaan voidaan oleta, että valon kulkema matka on meno ja palumatkan summa, eli laiteiden välinen etäisyys tulee olla korrostettuna kahdella. tällöin saadaan nopeudeksi 2,8*108m/s.
1-6 b)
b)
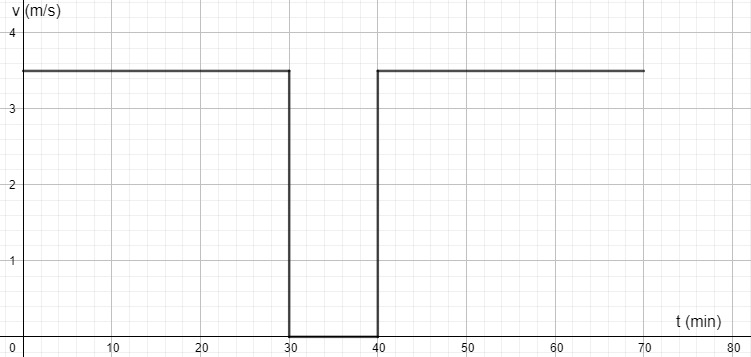
1-7











1-8







V: b) 1,3 m/s
1-9




1-14
a)

b)

a) 10s-20s
b) 30s-40s
c) 10s-10s, 20s-30s, 40s-50s
d) 30s-40s
1-2
a) 2,0 m
b) 2,0 m/s
c) -6,0 m
d) 6,0 m/s, taaksepäin
e) -4,0 m/s
1-3
a) Nopeus kasvaa nopeasti välillä 0s-2s. sitten nopeus laskee ja kappale alkaa liikkumaan taaksepäin.
b) 12m
c)
d)

1-4
a)
Teoreettinen nopeus:
Oikea nopeus:

b)

1-5

Kokkeen toiminnasta sanottiin, että ''Valonnopeuden mittauslaite lähettää valopulssiin ja vastaanottaa peilistä takaisin heijastuneen pulssin sekä rekisteröi pulssin lähdön ja paluun väliseen aikaeron. Kokeessa peilin etäisyyttä (s) mittalaitteesta muutettiin metrin välein ja mitattiin aikaerot (t), jolloin saatiin alla olevan taulukon mukaiset tulokset.''. Tämän mukaan voidaan oleta, että valon kulkema matka on meno ja palumatkan summa, eli laiteiden välinen etäisyys tulee olla korrostettuna kahdella. tällöin saadaan nopeudeksi 2,8*108m/s.
1-6

1-7

1-8
V: b) 1,3 m/s
1-9
1-14
a)
b)