Teoria T1 Pituuden, pinta-alan ja tilavuuden mittayksiköt
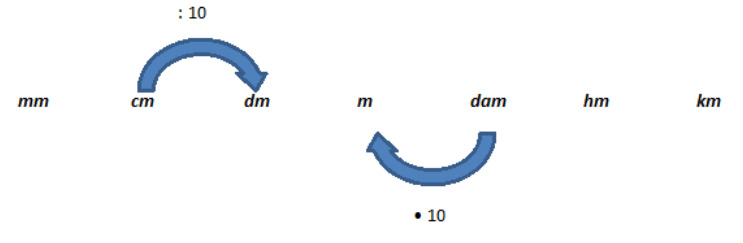
Pituuden mittayksiköt:
millimetri (mm), senttimetri (cm), desimetri (dm), metri (m), dekametri (dam), hehtometri (hm), kilometri (km)
[[$ 12 $]]km [[$ =12 \cdot 10 \cdot 10 \cdot 10 $]]m [[$ = 12000 $]]m.
Tällöin siis yksiköstä km siirrytään kolme yksikköä pienempää mittayksikköön m, jolloin kilometrimäärä kerrotaan kolme kertaa peräkkäin luvulla 10.
[[$ 150 $]]cm [[$ = 150 : 10 : 10 = 1,5 $]]m
Tällöin siis yksiköstä cm siirrytään kaksi yksikköä suurempaan mittayksikköön m, jolloin senttimetrit jaetaan kaksi kertaa peräkkäin luvulla 10.
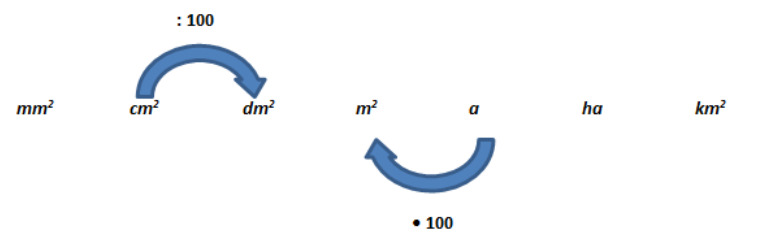
Pinta-alan mittayksiköt:
neliömillimetri ([[$ mm^2 $]]), neliösenttimetri ([[$ cm^2 $]]), neliödesimetri ([[$ dm^2 $]]), neliömetri ([[$ m^2 $]]), aari (a), hehtaari (ha), neliökilometri ([[$ km^2 $]])
[[$ 1,2 m^2 = 1,2 \cdot 100 \cdot 100 = 12000 cm^2 $]]
Tällöin siis yksiköstä [[$ m^2 $]] siirrytään kaksi yksikköä pienempää mittayksikköön [[$ cm^2 $]], jolloin neliömetrit kerrotaan kaksi kertaa peräkkäin luvulla 100.
[[$ 120 ha = 120 : 100 = 1,2 km^2$]]
Tällöin siis yksiköstä [[$ ha $]] siirrytään yksi yksikkö suurempaan mittayksikköön [[$ km^2 $]], jolloin hehtaarit jaetaan yhden kerran luvulla 100.
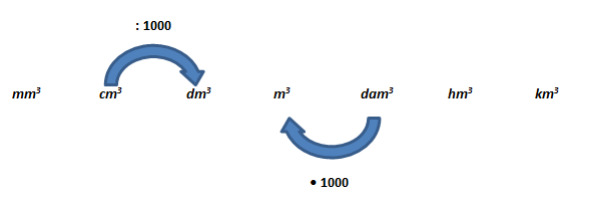
Tilavuuden mittayksiköt:
kuutiomillimetri ([[$ mm^3 $]]), kuutiosenttimetri ([[$ cm^3 $]]), kuutiodesimetri ([[$ dm^3 $]]), kuutiometri ([[$ m^3 $]])
[[$ 2,3 m^3 = 2,3 \cdot 1000 \cdot 1000 = 2300000 cm^2$]]
Tällöin siis yksiköstä [[$ m^3 $]] siirrytään kaksi yksikköä pienempää mittayksikköön [[$ cm^3 $]], jolloin kuutiometrit kerrotaan kaksi kertaa peräkkäin luvulla 1000.
[[$ 350mm3=350 : 1000 = 0,350 cm3$]]
Tällöin siis yksiköstä [[$ mm^3 $]] siirrytään yksi yksikkö suurempaan mittayksikköön [[$ cm^3 $]], jolloin kuutiomillimetrit jaetaan yhden kerran luvulla 1000.
millimetri (mm), senttimetri (cm), desimetri (dm), metri (m), dekametri (dam), hehtometri (hm), kilometri (km)
- Pituuden mittayksiköissä suudempi yksikkö sisältää aina 10 kappaletta pienempää mittayksikköä.
- Esimerkiksi yhdessä senttimetrissä on kymmenen kappaletta millimetrin mittaisia osia eli 1 cm = 10 mm.
- Kun pituuden yksiköitä muutetaan suuremmasta yksiköstä pienempään yksikköön kerrotaan luku 10.
- Kun pituuden yksiköitä muutetaan pienemmästä yksiköstä suurempaan yksikköön jaetaan luku 10.
[[$ 12 $]]km [[$ =12 \cdot 10 \cdot 10 \cdot 10 $]]m [[$ = 12000 $]]m.
Tällöin siis yksiköstä km siirrytään kolme yksikköä pienempää mittayksikköön m, jolloin kilometrimäärä kerrotaan kolme kertaa peräkkäin luvulla 10.
[[$ 150 $]]cm [[$ = 150 : 10 : 10 = 1,5 $]]m
Tällöin siis yksiköstä cm siirrytään kaksi yksikköä suurempaan mittayksikköön m, jolloin senttimetrit jaetaan kaksi kertaa peräkkäin luvulla 10.

Pinta-alan mittayksiköt:
neliömillimetri ([[$ mm^2 $]]), neliösenttimetri ([[$ cm^2 $]]), neliödesimetri ([[$ dm^2 $]]), neliömetri ([[$ m^2 $]]), aari (a), hehtaari (ha), neliökilometri ([[$ km^2 $]])
- Pinta-alan yksiköissä suudempi yksikkö sisältää aina 100 kappaletta pienempää mittayksikköä.
- Tämä siksi, koska neliön pinta-ala on sivu kertaa sivu eli tässä tapauksessa [[$ 10 \cdot 10 = 100 $]].
- Esimerkiksi yhdessä neliösenttimetrissä on satakappaletta neliömillimetrin kokoisia osia eli [[$ 1 cm^2 = 100 mm^2 $]].
- Aari a tarkoittaa aluetta, jonka pinta-ala on [[$ 10m \cdot 10m = 100m^2 $]].
- hehtaari ha tarkoittaa aluetta, jonka pinta-ala on [[$ 100m \cdot 100m = 10000m^2 $]].
- Kun pinta-alan yksiköitä muutetaan suuremmasta yksiköstä pienempään yksikköön kerrotaan luku 100.
- Kun pinta-alan yksiköitä muutetaan pienemmästä yksiköstä suurempaan yksikköön jaetaan luku 100.
[[$ 1,2 m^2 = 1,2 \cdot 100 \cdot 100 = 12000 cm^2 $]]
Tällöin siis yksiköstä [[$ m^2 $]] siirrytään kaksi yksikköä pienempää mittayksikköön [[$ cm^2 $]], jolloin neliömetrit kerrotaan kaksi kertaa peräkkäin luvulla 100.
[[$ 120 ha = 120 : 100 = 1,2 km^2$]]
Tällöin siis yksiköstä [[$ ha $]] siirrytään yksi yksikkö suurempaan mittayksikköön [[$ km^2 $]], jolloin hehtaarit jaetaan yhden kerran luvulla 100.

Tilavuuden mittayksiköt:
kuutiomillimetri ([[$ mm^3 $]]), kuutiosenttimetri ([[$ cm^3 $]]), kuutiodesimetri ([[$ dm^3 $]]), kuutiometri ([[$ m^3 $]])
- Tilavuuden mittayksiköissä suudempi yksikkö sisältää aina 1000 kappaletta pienempää mittayksikköä.
- Tämä siksi, koska kuution tilavuus on sivu kertaa sivu kertaa sivu eli tässä tapauksessa [[$ 10 \cdot 10 \cdot 10 = 1000 $]].
- Esimerkiksi yhdessä kuutiometrissä on tuhat kappaletta kuutiodesimetrejä [[$ 1 m^3 = 1000 dm^3 $]].
- Yksi kuutiodesimetri on sama kuin yksi litra eli [[$ 1dm^3=1l $]], jolloin yksi kuutio metri on 1000 litraa eli [[$ 1 m^3 = 1000 dm^3 = 1000l$]].
- Yksi kuutiosenttimetri on sama kuin yksi millilitra eli [[$ 1cm^3=1ml $]].
- Kun tilavuuden yksiköitä muutetaan suuremmasta yksiköstä pienempään yksikköön kerrotaan luku 1000.
- Kun tilavuuden yksiköitä muutetaan pienemmästä yksiköstä suurempaan yksikköön jaetaan luku 1000.
[[$ 2,3 m^3 = 2,3 \cdot 1000 \cdot 1000 = 2300000 cm^2$]]
Tällöin siis yksiköstä [[$ m^3 $]] siirrytään kaksi yksikköä pienempää mittayksikköön [[$ cm^3 $]], jolloin kuutiometrit kerrotaan kaksi kertaa peräkkäin luvulla 1000.
[[$ 350mm3=350 : 1000 = 0,350 cm3$]]
Tällöin siis yksiköstä [[$ mm^3 $]] siirrytään yksi yksikkö suurempaan mittayksikköön [[$ cm^3 $]], jolloin kuutiomillimetrit jaetaan yhden kerran luvulla 1000.
