Tasokuvioiden pinta-aloja (1h)
Peda.net tehtävä P1 Tasokuvioiden pinta-aloja
Teoria T1 Suunnikkaiden pinta-aloja
Suunnikas on nelikulmio, jonka vastakkaiset sivut ovat yhdensuuntaiset.
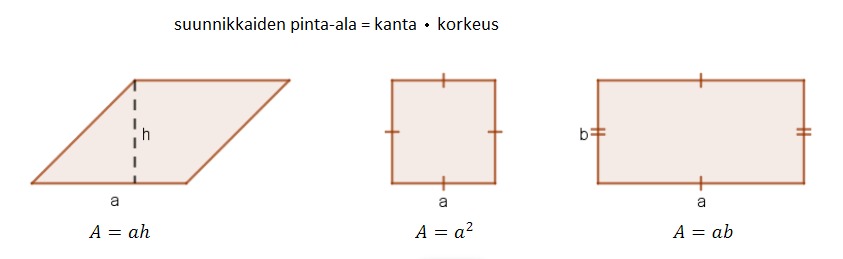
- Suorakulmio on suunnikkaan erikoistapaus, jossa vastakkaiset sivut ovat yhtä pitkät ja kaikki kulmat 90 astetta (suorakulma).
- Neliö on suunnikkaan erikoistapaus, jossa kaikki sivut ovat yhtäpitkät ja kaikki kulmat 90 astetta (suorakulma).

Teoria T2 Kolmioiden pinta-aloja
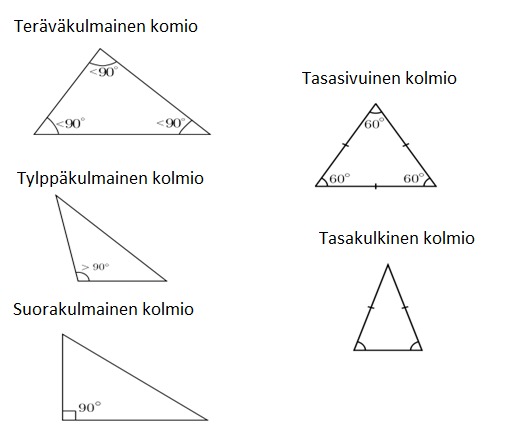
Kolmiot voidaan luokitella kulman suuruuden mukaan tai sivujen pituuksien mukaan:
Oli kolmio minkälainen hyvänsä, pinta-ala lasketaan aina samalla tavalla eli kanta kertaa korkeus jaettuna kahdella. Kolmion pinta-ala muodostuu, kun suunnikas jaetaan kahteen yhtäsuureen osaan, jolloin pinta-ala on suunnikkaan pinta-ala jaettuna kahdella. Huom! tylppäkulmaisen kolmion tapauksessa korkeusjana eli kohtisuora etäisyys kolmion kannasta kolmion kärkipisteeseen ei sijaitse kolmion sisällä.

- Teräväkulmainen kolmio: kaikki kulmat alle 90 astetta.
- Tylppäkulmainen kolmio: yksi kulma yli 90 astetta.
- Suorakulmainen kolmio: yksi kulma tasan 90 astetta.
- Tasasivuinen kolmio: kaikki sivut yhtä pitkät, kaikki kulmat yhtä suuret eli [[$ \frac{180^{o}}{3}=60^{o} $]].
- Tasakylkinen kolmio: molemmat kyljet yhtä pitkät, kantakulmat yhtä suuret.

Oli kolmio minkälainen hyvänsä, pinta-ala lasketaan aina samalla tavalla eli kanta kertaa korkeus jaettuna kahdella. Kolmion pinta-ala muodostuu, kun suunnikas jaetaan kahteen yhtäsuureen osaan, jolloin pinta-ala on suunnikkaan pinta-ala jaettuna kahdella. Huom! tylppäkulmaisen kolmion tapauksessa korkeusjana eli kohtisuora etäisyys kolmion kannasta kolmion kärkipisteeseen ei sijaitse kolmion sisällä.

Teoria T3 Puolisuunnikkaan pinta-ala
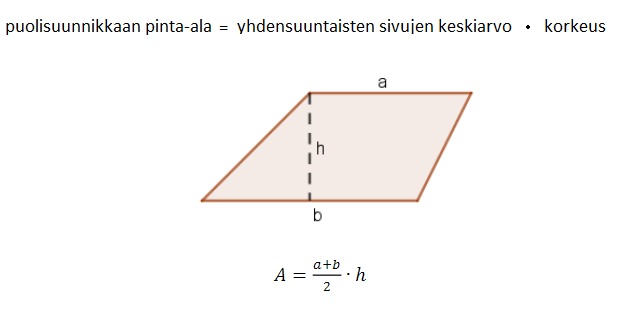
- Puolisuunnikas on nelikulmio, jossa jommat kummat vastakkaisista sivuista ovat yhdensuuntaiset.
- Puolisuunnikkaan pinta-ala lasketaan laskemalla ensin vastakkaisten sivujen pituudet yhteen, jakamalla tulos kahdella ja kertomalla se puolisuunnikkaan korkeudella.
- Toisin sanoen lasketaan ensin yhdensuuntaisten sivujen keskiarvo joka kerrotaan puolisuunnikkaan korkeudella.
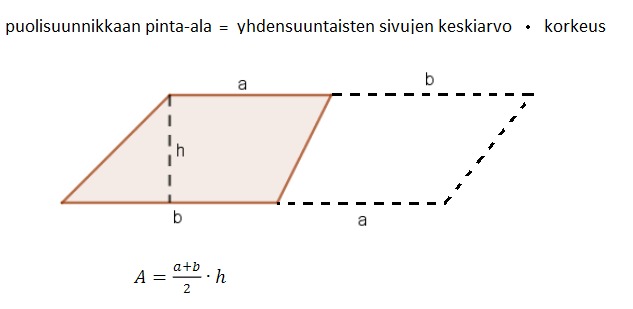
- Kaava voidaan perustella ottamalla toinen samanlainen puolisuunnikas ja asettamalla se edellisen puolisuunnikkaan jatkoksi toisin päin käännettynä. Tällöin saadaan suunnikas, jonka kanta on a+b. Suunnikkaan pinta-ala lasketaan kanta kertaa korkeus, mutta saadaksemme pelkän puolisuunnikkaan pinta-alan, on tulos jaettava vielä kahteen osaan.
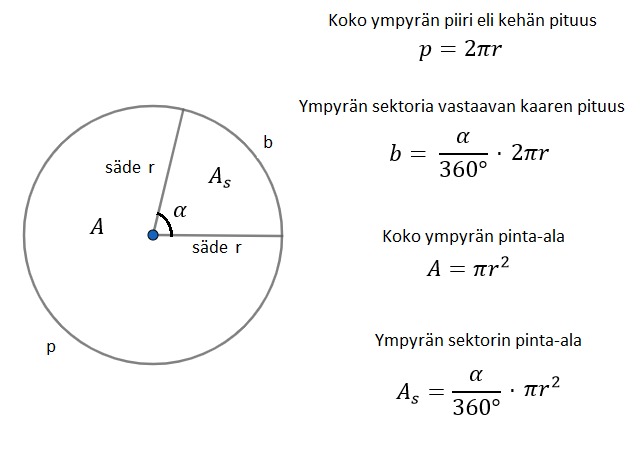
Teoria T4 Ympyrän ja ympyrästä otetun sektorin piiri ja pinta-ala
- Piiri tarkoittaa ympärysmittaa. Esimerkiksi kasvimaan piiri tarkoittaa, kuinka monta metriä joudut kävelemään kasvimaan reunaa pitkin, ennen kuin pääset takaisin lähtöpisteeseesi.
- Kaikilla edellä mainituilla tasokuvioilla piiri lasketaan samalla tavalla eli kaikkien sivujen pituudet lasketaan yhteen.
- Ympyrän tapauksessa piiri lasketaan ympyrän säteen r ja luvun pii [[$ \pi $]] avulla.
- Aikaisemmista kursseita muistamme, että luku pii on ympyrän kehän pituuden ja halkaisian välinen suhde eli jakolasku [[$ \pi =\frac{p}{d}$]]. Jokaisella ympyrällä kehän pituuden suhde halkaisijaan on sama eli vakio.
- Koska ympyrän asteluku on 360°, ympyrästä lohkaistun pitsasiivun eli sektorin kehän pituus on vastaava osa sektorin asteluvusta.
- Jos sektorin asteluku on 60°, on sektorin kaaren pituus kuusi kertaa pienempi kuin koko ympyrän piiri.
- Sama tulos pätee myös ympyrän pinta-alan kohdalla.
Esimerkki 1: Ympyrän säde r on 5 cm. Laske ympyrän pinta-ala ja piiri.
Ratkaisu:
Piiri: Käytetään ympyrän piirin kaavaa, jolloin saadaan
[[$ p=2 \pi r = 2 \cdot \pi \cdot r = 2 \cdot \pi \cdot 5 = 31,459... \approx 31,5$]]cm.
Pinta-ala: Käytetään ympyrän pinta-alan kaavaa, jolloin saadaan
[[$ A = \pi \cdot r^2 = \pi \cdot r \cdot r = \pi \cdot 5 \cdot 5 = 78,539... \approx 78,5 cm^2.$]]
Esimerkki 2: Laske edellisestä ympyrästä lohkaistun sektorin kaaren pituus ja pinta-ala, kun sektorin keskuskulma on 40 astetta.
Ratkaisu:
Koko ympyrän asteluku on 360°, joten 40° menee yhteensä 9 kertaa 360° asteeseen. Kysytyn sektorin kaaren pituus on siis yhdeksän kertaa pienempiä kuin koko ympyrän.
sektorin kaaren pituus:
[[$ b= \frac{p}{9} = \frac{2 \pi r}{9} =\frac{31,459...}{9} = 3,4954444... \approx 3,5 $]]cm
Samaan tulokseen päästään myös sektorin kaaren pituuden laskukaavan avulla, jolloin
[[$ b = \frac{\alpha}{360^o} \cdot 2 \pi r = \frac{40^o}{360^o} \cdot 31,459... = 3,4954444... \approx 3,5$]]cm
sektorin pinta-ala:
Koko ympyrän asteluku on 360°, joten 40° menee yhteensä 9 kertaa 360° asteeseen. Kysytyn sektorin pinta-ala on siis yhdeksän kertaa pienempiä kuin koko ympyrän.
[[$ A_s= \frac{A}{9} = \frac{\pi r^2}{9} =\frac{78,539...}{9} = 8,726555... \approx 8,7 cm^2$]]
Samaan tulokseen päästään myös sektorin pinta-alan laskukaavan avulla, jolloin
[[$ A = \frac{\alpha}{360^o} \cdot \pi r^2 = \frac{40^o}{360^o} \cdot 78,538... = 8,726555... \approx 8,7 cm^2$]]