Perustehtävät (kaikki tekee)

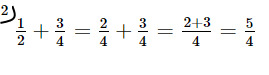
Laskettaessa murtolukuja yhteen täytyy murtolukujen olla samannimisiä. Tällöin siis murtoviivan alla olevien lukujen eli nimittäjien tulee olla samat. Jos murtolukujen nimittäjät ovat erisuuret tulee murtoluvut laventaa tai supistaa samannimisiksi.

Muuta sekaluvut murtoluvuksi ennen yhteen- ja vähennyslaskua.

Esimerkki 1. Samannimiset murtoluvut lasketaan yhteen siten, että osoittajat lasketaan yhteen. Nimittäjäksi merkitään yhteinen nimittäjä.

[[$ \frac{2}{3}+\frac{1}{3} = \frac{2+1}{3} = \frac{3}{3} =1 $]]​

Esimerkki 2. Erinimiset murtoluvut muutetaan ensin samannimisiksi laventamalla tai supistamalla ja sitten lasketaan yhteen.



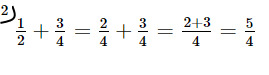
Laske.
a) [[$ \frac{3}{5}+\frac{1}{5} = $]]​

b) [[$ \frac{5}{6}-\frac{3}{6} = $]]​

c) [[$ \frac{3}{4} + \frac{2}{3} = $]]​


Kirjantehtävät

7 tehtävät oppikirjan s.21-22 tehtävät 1,2,3,4,21,23,27

8 tehtävät oppikirjan s.21-23 tehtävät 21,23,24,27,42

9 tehtävät oppikirjan s.22-23 tehtävät 32,36,38,49,50

10 tehtävät oppikirjan s.199 tehtävät 64,65,67,68,74