• Murtoluku saadaan, kun kaksi kokonaislukua jaetaan keskenään.
• Murtoluku on siis kahden kokonaisluvun osamäärä.
• Esimerkiksi luku 2 jaetaan luvulla 5 saadaan murtoluku kaksi viidesosaa, joka merkataan matemaattisesti [[$ 2 : 5 = \frac{2}{5} $]]​.
• Jakolaskuista puhuttaessa voi käyttää joko kaksoispistettä tai murtoviivaa, mutta murtoluvuista puhuttaessa käytetään murtoviivaa jakolaskun merkiksi.
• Murtolukuja voidaan merkitä matemaattisesti, sanallisesti tai kuvallisesti.

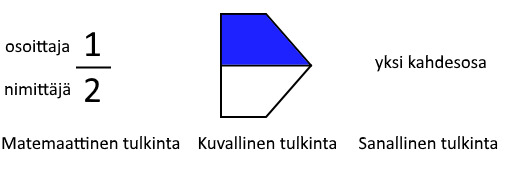
Perustehtävät (kaikki tekee)

1. Kirjoita vihkoosi alla olevista kuvista murtolukujen matemaattinen ja sanallinen tulkinta.


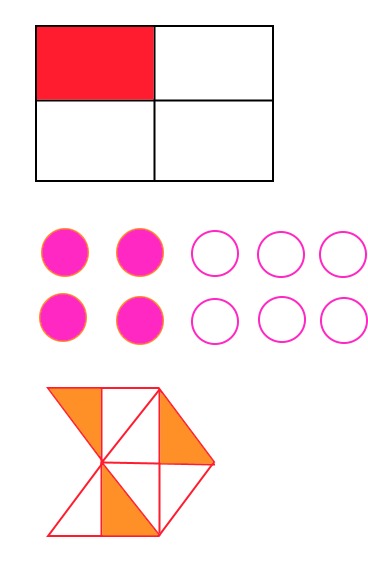
2. Piirrä seuraavat murtoluvut vihkoosi.

a) kolme viidesosaa

b) [[$ \frac{4}{7} $]]​


3. Murtoluvun laventaminen tarkoittaa, että osoittaja ja nimittäjä kerrotaan samalla luvulla. Lavennettaessa murtoluvun suuruus säilyy samana.



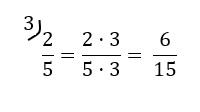
Lavenna murtoluku [[$ \frac{3}{7} $]]​ kertomalla osoittaja ja nimittäjä luvulla 2.

4. Murtoluvun supistaminen tarkoittaa, että osoittaja ja nimittäjä jaetaan samalla luvulla. Supistettaessa murtoluvun suuruus säilyy samana. Supista murtoluku [[$ \frac{5}{15} $]]​.


5. (9-10 tavoittelijat tekee) Yhdistä kirjaimet ja numerot toisiinsa.


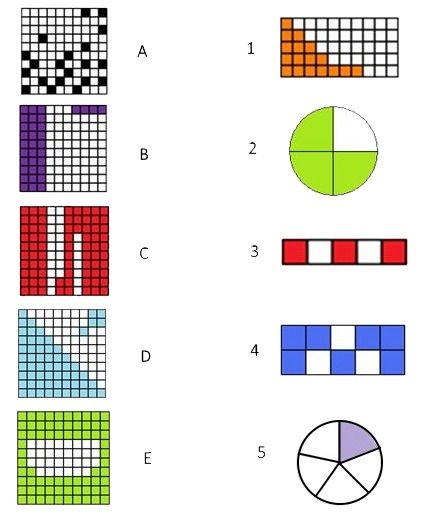
Kirjan tehtävät

7 tehtävät oppikirjan s. 17 tehtävät 1,2,6,8,12

8 tehtävät oppikirjan s. 17 tehtävät 1,3,6,8,9,10,12

9 tehtävät oppikirjan s. 17 tehtävät 3,5,9,10,13,15

10 tehtävät oppikirjan s. 197 tehtävät 46,47,48,50,52