5.4 Geometrinen lukujono

Geometrinen lukujono


Geometrisessa lukujonossa kahden peräkkäisen jäsenen suhde on vakio eli jäsen saadaan kertomalla edellinen jäsen jollakin vakiolla.
Tätä vakiota kutsutaan suhdeluvuksi [[$ q $]].​

Geometrisen lukujonon suhdeluku [[$ q $]] saadaan määritettyä kaavalla

[[$ q=\dfrac{a_n}{a_{n-1}} $]]



Tällöin geometrinen lukujono ilmoitettuna rekursiivisesti on
[[$a_n=a_{n-1} \cdot q$]]

1. jäsen on [[$a_1$]]
2. jäsen [[$a_2=a_1 \cdot q$]]
3. jäsen [[$a_3=a_2 \cdot q=a_1 \cdot q \cdot q=a_1 \cdot q^2$]]
4. jäsen [[$a_4=a_3 \cdot q=a_1 \cdot q^2 \cdot q=a_1 \cdot q^3$]]
[[$n$]]. jäsen [[$a_n=a_1 \cdot q^{n-1}$]]

Geometrinen lukujono ilmoitetaan yleensä yllä olevan analyyttisen säännön avulla.


Geometrisen lukujonon yleinen jäsen saadaan kaavalla

[[$ a_n=a_1 \cdot q^{n-1} $]]

jossa
[[$ a_n $]] on yleinen jäsen
​[[$ a_1 $]] on ensimmäinen jäsen
[[$ q $]] on peräkkäisten jäsenten suhde
[[$ n $]] on jäsenten lukumäärä

Peräkkäisten jäsenten suhde q

Jos [[$q=0$]], niin lukujono on [[$a_1,0,0,0,...$]], koska mikä tahansa luku kertaa nolla on nolla:
[[$a_n=a_{n-1} \cdot 0 =0$]].

Tämä lukujono ei kuitenkaan ole geometrinen, koska kahden peräkkäisen jäsenen osamäärän pitäisi olla vakio. Tässä tapauksessa [[$q$]] olisi [[$\frac{0}{0}$]], mutta nollalla ei voi jakaa.
Tästä päätellen geometrisessa lukujonossa [[$q$]] ei voi olla nolla eli [[$q \neq 0$]].

Jos [[$ q=1 $]], lukujono on [[$ a_1, a_1, a_1,... $]], koska mikä tahansa luku kerrottuna yhdellä on tämä luku: [[$ a_n=a_{n-1} \cdot 1=a_{n-1} $]].

  • Jos [[$ 0<q<1 $]], lukujono lähestyy nollaa.
    • Esimerkki geometrisesta lukujonosta, jossa [[$ a_1>0 $]] ja [[$ 0<q<1 $]].

    • Esimerkki geometrisesta lukujonosta, jossa [[$ a_1<0 $]] ja [[$ 0<q<1 $]].


  • Jos [[$ q>1 $]], lukujono kasvaa eksponentiaalisesti. Mitä suurempi on [[$ q $]], sitä jyrkemmin kuvaaja nousee.
    • Esimerkki geometrisesta lukujonosta, jossa [[$ a_1>0 $]] ja [[$ q>1 $]].
    • Esimerkki geometrisesta lukujonosta, jossa [[$ a_1<0 $]] ja [[$ q>1 $]].

    • Esimerkki geometrisesta lukujonosta, jossa [[$ -1<q<0 $]].

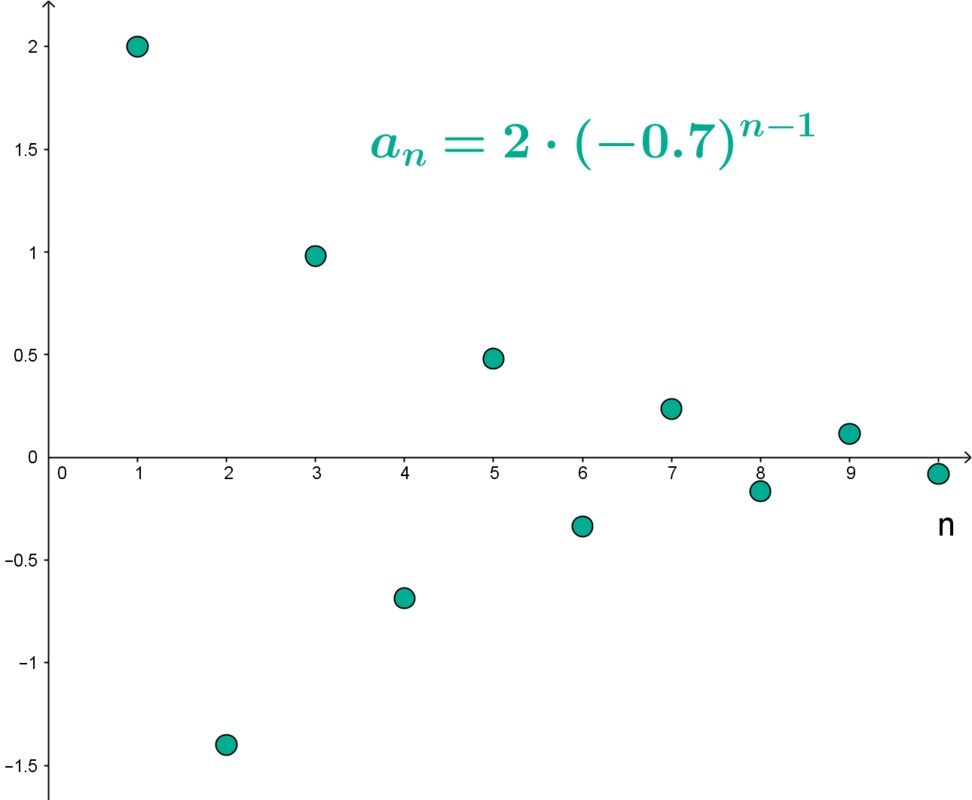
  • Jos [[$ q<-1 $]], lukujono lähestyy positiivista ([[$ \infty $]]) ja negatiivista ääretöntä ([[$ -\infty $]]).

    • Esimerkki geometrisesta lukujonosta, jossa [[$ q<-1 $]].

GeoGebra-sovelma geometrisesta lukujonosta

Alla olevalla sovelmalla voit kokeilla miten lukujono muuttuu, kun muutat ensimmäisen jäsenen ja suhdeluvun [[$q$]]. Huomaa, että lukuun tulee pilkun paikalle piste.



Esimerkki 1

Onko lukujono [[$ 4, 12, 48, 240,... $]]​ aritmeettinen tai geometrinen?

Ratkaisu:
Määritetään peräkkäisten jäsenten erotus [[$ d $]]​.
Lukujonon Peräkkäisten jäsenten erotus
[[$ n $]]​[[$ a_n $]]​[[$ d $]]​
[[$1$]] [[$4$]]
[[$2$]] [[$12$]] [[$ d=12-4=8 $]]​
[[$3$]] [[$48$]] [[$ d=48-12=36 $]]
[[$4$]] [[$240$]] [[$ d=240-48=192 $]]
Koska peräkkäisten jäsenten erotus [[$ d $]]​ ei ole vakio, lukujono ei ole aritmeettinen.

Määritetään peräkkäisten jäsenten suhde [[$ q $]]​.
Lukujonon Peräkkäisten jäsenten suhde
[[$ n $]]​[[$ a_n $]]​suhde [[$ q $]]​
[[$1$]] [[$4$]]
[[$2$]] [[$12$]] [[$ \begin{align}q&=\frac{12}{4}&=3 \\ && \end{align}$]]​
[[$3$]] [[$48$]] [[$ \begin{align}q&=\frac{48}{12}&=4 \\&&\end{align} $]]
[[$4$]] [[$240$]] [[$ \begin{align}q&=\frac{240}{48}&=5 \\ &&\end{align} $]]
Peräkkäisten jäsenten suhde [[$ q $]] ei ole vakio, joten lukujono ei ole myöskään geometrinen.

Vastaus: Lukujono ei ole aritmeettinen eikä geometrinen.

Esimerkki 2

Esitä geometrinen lukujono (931, 133, 19,...) rekursiivisesti ja analyyttisesti.

Ratkaisu:
Ratkaistaan suhdeluku [[$ q $]]​.
[[$ q=\dfrac{a_2}{a_1}=\dfrac{133}{931}=\dfrac{1}{7} $]]

Rekursiivinen sääntö on
[[$ \begin{cases}a_1=931\\a_n=\frac{1}{7} \cdot a_{n-1} & \quad n=2,3,4,...\end{cases} $]]

Analyyttinen sääntö on
[[$a_n=931 \cdot (\frac{1}{7})^{n-1}$]]

Esimerkki 3

Määritä geometrisen lukujonon ​[[$ -\frac{4}{9}, \frac{4}{3}, -4,... $]] kymmenes jäsen.

Ratkaisu:
[[$ -\frac{4}{9}, \frac{4}{3}, -4,... $]]
[[$ q=\dfrac{a_{n+1}}{a_n}=\dfrac{a_2}{a_1}=\dfrac{\frac{4}{3}}{-\frac{4}{9}}=\frac{4}{3} \cdot (-\frac{9}{4})=-\frac{9}{3}=-3 $]]

(Muistathan, että murtolukujen jakolasku muutetaan kertolaskuksi kertomalla jakaja jaettavan käänteisluvulla)

Kymmenes jäsen
[[$ a_{10}=a_1 \cdot q^{10-1}=-\frac{4}{9} \cdot(-3)^9=8748 $]]

Vastaus: Kymmenes jäsen on 8748.

Esimerkki 4

Määritä geometrisen lukujonon kuudes jäsen, kun viides jäsen on [[$ -196 $]]​ ja seitsemäs jäsen on [[$ -36 $]].

Ratkaisu:
[[$ \begin{align}a_6&=q \cdot a_5\\a_7&=q \cdot a_6=q \cdot q \cdot a_5\\-36&=q^2 \cdot (-196) & \parallel &:(-196)\\q^2&=\frac{-36}{-196}=\frac{9}{49}\\q&=\pm \sqrt{\frac{9}{49}}=\pm \frac{3}{7} \end{align} $]]​

Määritetään kuudes jäsen, kun [[$ q=\frac{3}{7} $]]:
[[$ a_6=q \cdot a_5=\frac{3}{7} \cdot (-196)=-84 $]]

Huom! Jos [[$ q=-\frac{3}{7} $]], niin [[$ q^2=\frac{9}{49} $]] eli myös [[$ q=-\frac{3}{7} $]] kelpaa.

Tällöin [[$ a_6=-\frac{3}{7} \cdot (-196)=84 $]]

Tarkistetaan vastaus:
[[$ a_7=-\frac{3}{7} \cdot 84=-36 $]] eli pitää paikkansa.

Vastaus: [[$ a_6=$]] –84 tai 84.

Esimerkki 5

Geometrisen lukujonon toinen jäsen on 180 ​ja peräkkäisten jäsenten suhde [[$ q $]] on [[$ \frac{1}{3} $]]​. Määritä jonon kahdeksas ja [[$ n $]]:s jäsen.

Ratkaisu:
[[$ a_2=180 $]]
[[$ q=\frac{1}{3} $]]

Toinen jäsen on [[$a_2=a_1 \cdot q$]].
Tällöin ensimmäinen jäsen on [[$a_1=\dfrac{a_2}{q}=\dfrac{180}{\frac{1}{3}}=180 \cdot 3=540$]]

Kahdeksas jäsen on [[$a_8=a_1 \cdot q^{n-1}=540 \cdot \frac{1}{3}^7 \approx \text{0,2469}$]]

[[$ n $]]:s jäsen on
[[$ a_n=a_1 \cdot q^{n-1}=540 \cdot (\frac{1}{3})^{n-1} $]]

Vastaus: Kahdeksas jäsen on 0,25 ja [[$ n $]]:s jäsen on [[$ 540 \cdot (\frac{1}{3})^{n-1} $]].

Esimerkki 6

Määritä [[$ k $]]​, kun lukujono ([[$ -25, k, -49,... $]]​) on geometrinen.

Ratkaisu:
Peräkkäisten jäsenten suhde [[$ q $]] on vakio.
[[$ q=\dfrac{a_2}{a_1}=\dfrac{a_3}{a_2} $]]
[[$ \dfrac{k}{-25}=\dfrac{-49}{k} $]]

Määrittelyehto:
Nimittäjä ei saa olla nolla, joten [[$ k \neq 0 $]].

Kerrotaan ristiin, jolloin saadaan
[[$ \begin{align} k^2&=-25 \cdot (-49)=1225 & \parallel \sqrt{}\\k&=\pm 35 \end{align} $]]

Vastaus: [[$ k=\pm 35 $]]