Todennäköisyys
Osion Todennäköisyys tehtävät löytyvät täältä.
Puukaavio
Erilaisten vaihtoehtojen lukumäärää voidaan hahmotella niin kutsutun puukaavion avulla.
Esimerkki: Mielesi tekee ruoaksi joko kalaa tai kasvispyöryköitä. Kuinka monta mahdollista ruokavaihtoehtoa sinulla on, kun ruokakaapistasi löytyy lisäksi riisiä, spagettia, perunoita ja tattaria?
Ratkaisu: Tehdään tilanteesta puukaavio:
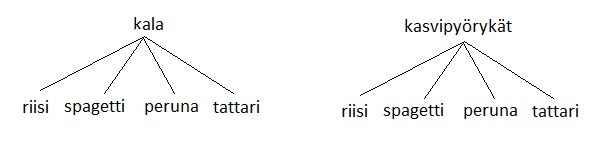
Kummallakin pääruokavaihtoehdolla on siis neljä mahdollista lisuketta, joten kaikkiaan vaihtoehtoja on [[$ 2 \cdot 4 = 8. $]]
Esimerkki: Mielesi tekee ruoaksi joko kalaa tai kasvispyöryköitä. Kuinka monta mahdollista ruokavaihtoehtoa sinulla on, kun ruokakaapistasi löytyy lisäksi riisiä, spagettia, perunoita ja tattaria?
Ratkaisu: Tehdään tilanteesta puukaavio:

Kummallakin pääruokavaihtoehdolla on siis neljä mahdollista lisuketta, joten kaikkiaan vaihtoehtoja on [[$ 2 \cdot 4 = 8. $]]
Tuloperiaate
- Tuloperiaate on lyhyempi ilmaisu puukaaviolla saatujen vaihtoehtojen määrän ilmoittamiselle.
- Kun vaihtoehtoja on paljon, puukaavion tekeminen on työlästä ja aikaavievää.
- Tällöin vaihtoehtojen lukumäärän saamiseksi kannattaa käyttää tuloperiaatetta, jossa erilaisten vaihtoehtojen lukumäärä saadaan kertomalla yksittäisten vaihtoehtojen lukumäärät keskenään.
Ratkaisu:
Pankkikortin tunnusluvun ensimmäiselle numerolle on 10 mahdollista vaihtoehtoa.
Pankkikortin tunnusluvun toiselle numerolle on 10 mahdollista vaihtoehtoa.
Pankkikortin tunnusluvun kolmannelle numerolle on 10 mahdollista vaihtoehtoa.
Pankkikortin tunnusluvun neljännelle numerolle on 10 mahdollista vaihtoehtoa.
Tällöin siis tuloperiaatten mukaisesti kaikkiaan vaihtoehtoja on [[$ 10 \cdot 10 \cdot10 \cdot 10 = 10000 $]]
Valitaan vain osa
Tämän tyyppiset tehtävät lasketaan tuloperiaatteen avulla. Tässä neljä erilaista esimerkkiä tuloperiaatteen käytöstä.
Kuinka moneen erilaiseen jonoon 4 henkilöä voidaan asettaa? Ensimmäinen jonon jäsen voidaan valita neljällä eri tavalla. Nyt yksi on jo valittu, joten seuraava jonon jäsen voidaan valita kolmella eri tavalla, kolmas jäsen kahdella ja viimeinen jäsen yhdellä tavalla. Tuloperiaatteen mukaisesti saadaan [[$ 4 \cdot 3 \cdot 2 \cdot 1 = 24 $]], joista jokainen muodostunut jono on erilainen.
Kuinka monta erilaista tanssiparia saadaan 4 henkilöstä? Tuloperiaatteen mukaisesti [[$ 4 \cdot 3 = 12 $]]. Nyt tulos täytyy kuitenkin jakaa kahdella, koska tanssipari voi olla kahdessa eri järjestyksessä (esim. tyttö ja poika on tässä esimerkissä sama kuin poika ja tyttö). Tällöin siis erilaisia tanssipareja on [[$ \frac{12}{2} = 6 $]].
Kuinka monella tavalla voit nostaa taskussasi olevat 10 sentin, 50 sentin ja 2 euron kolikot yksitellen käteesi. Nyt kolikot jäävät käteesi, eikä niitä palauteta takaisin taskuun. Tuloperiaatteen mukaisesti [[$ 3 \cdot 2 \cdot 1 = 6 $]].
Taskussasi on 10 sentin, 50 sentin ja 2 euron kolikot. Kuinka monta vaihtoehtoa on nostaa kolme kolikkoa, kun kolikot palautetaan takaisin taskuun noston jälkeen. Nyt kullakin nostolla on kolme mahdollista vaihtoehtoa. Tuloperiaatteen mukaisesti [[$ 3 \cdot 3 \cdot 3 = 27 $]].
Kuinka moneen erilaiseen jonoon 4 henkilöä voidaan asettaa? Ensimmäinen jonon jäsen voidaan valita neljällä eri tavalla. Nyt yksi on jo valittu, joten seuraava jonon jäsen voidaan valita kolmella eri tavalla, kolmas jäsen kahdella ja viimeinen jäsen yhdellä tavalla. Tuloperiaatteen mukaisesti saadaan [[$ 4 \cdot 3 \cdot 2 \cdot 1 = 24 $]], joista jokainen muodostunut jono on erilainen.
Kuinka monta erilaista tanssiparia saadaan 4 henkilöstä? Tuloperiaatteen mukaisesti [[$ 4 \cdot 3 = 12 $]]. Nyt tulos täytyy kuitenkin jakaa kahdella, koska tanssipari voi olla kahdessa eri järjestyksessä (esim. tyttö ja poika on tässä esimerkissä sama kuin poika ja tyttö). Tällöin siis erilaisia tanssipareja on [[$ \frac{12}{2} = 6 $]].
Kuinka monella tavalla voit nostaa taskussasi olevat 10 sentin, 50 sentin ja 2 euron kolikot yksitellen käteesi. Nyt kolikot jäävät käteesi, eikä niitä palauteta takaisin taskuun. Tuloperiaatteen mukaisesti [[$ 3 \cdot 2 \cdot 1 = 6 $]].
Taskussasi on 10 sentin, 50 sentin ja 2 euron kolikot. Kuinka monta vaihtoehtoa on nostaa kolme kolikkoa, kun kolikot palautetaan takaisin taskuun noston jälkeen. Nyt kullakin nostolla on kolme mahdollista vaihtoehtoa. Tuloperiaatteen mukaisesti [[$ 3 \cdot 3 \cdot 3 = 27 $]].
Todennäköisyys
- Todennäköisyys lasketaan jakamalla suotuisten vaihtoehtojen lukumäärä kaikilla mahdollisilla vaihtoehdoilla.
- Ilmoitetaan prosentteina (0-100%) tai lukuarvona (0-1).
- Mahdottoman tapahtuman todennäköisyys on 0.
- Varman tapahtuman todennäköisyys on 1.
- Klassinen todennäköisyys nimitystä käytetään teoreettisista laskuista ja Tilastollista todennäköisyyttä silloin, kun todennäköisyys lasketaan tiettyjen havaintojen pohjalta.
- Klassisen todennäköisyyden avulla ei voida esimerkiksi laskea sitä, kuinka todennäköisesti 10 vuotta vanha auto läpäisee katsastuksen. Tällöin on käytettävä apuna tilastoja.
- Klassinen ja Tilastollinen todennäköisyys lasketaan kuitenkin samalla tavalla.
Esimerkki: Olet unohtanut pankkikorttisi tunnusluvun. Kuinka todennäköistä on, että saat tunnusluvun oikein kolmella yrittämällä ennen, kuin pankkiautomaatti imaisee korttisi.
Ratkaisu: Edellisessä tehtävässä laskimme pankkikortin tunnusluvulle [[$ 10 \cdot 10 \cdot10 \cdot 10 = 10000 $]] vaihtoehtoa.
Käytössäsi on 3 yritystä eli suotuisia tapauksia on 3 kappaletta. Todennäköisyys onnistumiselle on siis
[[$ \frac{suotuiset \quad tapaukset}{kaikki \quad tapaukset} = \frac{3}{10000} =0,003. $]]
Aikaisemmin olemme oppineet, että 1% [[$= \frac{1}{100} = 0,01 $]]. Joten todennäköisyys onnistumiseen on 0,3%
Tuloperiaate
Apuja joihinkin kirjan tehtäviin
s.85
5 Lasketaan edellisen esimerkin tuloperiaatteen avulla. Pohdi, kuinka monta vaihtoehtoa on numerolukon ensimmäisellä, toisella, jne nunerolla ja ratkaise tehtävä tuloperiaatteen mukaisesti.
s. 90
8 Aiemmin olemme oppineet, että luonnolliset luvut ovat lukumäärää ilmoittavia lukuja (0,1,2,...). Pohdi, kuinka monta vaihtoehtoa on luonnollisen luvun ensimmäiselle, toiselle, jne numerolle ja ratkaise tehtävä tuloperiaatteen mukaisesti.
eli
Jos samaa numeroa voi käyttää useasti on ensimmäiseen lukuun neljä vaihtoehtoa samoin kuin toiseen ja kolmanteen. Jos samaa lukua ei saa käyttää uudestaan on ensimmäiseen lukuun neljä vaihtoehtoa toiseen lukuun 3 ja kolmanteen 2 vaihtoehtoa. Tehtävän annossa ei tätä mainita, joten tehtävän voi ymmärtäää molemmilla tavoilla.
13 a) Pohdi, kuinka monta vaihtoehtoa on ensimmäiselle, toiselle, jne nostolle, kun pallo palautetaan aina takaisin pöydälle. Ratkaise tehtävä tuloperiaatteen mukaisesti.
b) Nyt pallo jätetään palauttamatta, mikä vaikuttaa ensimmäisen noston jälkeisiin vaihtoehtojen lukumääriin. Pohdi, kuinka monta vaihtoehtoa on ensimmäiselle, toiselle, jne nostolle, kun pallo palautetaan aina takaisin pöydälle. Ratkaise tehtävä tuloperiaatteen mukaisesti.
5 Lasketaan edellisen esimerkin tuloperiaatteen avulla. Pohdi, kuinka monta vaihtoehtoa on numerolukon ensimmäisellä, toisella, jne nunerolla ja ratkaise tehtävä tuloperiaatteen mukaisesti.
s. 90
8 Aiemmin olemme oppineet, että luonnolliset luvut ovat lukumäärää ilmoittavia lukuja (0,1,2,...). Pohdi, kuinka monta vaihtoehtoa on luonnollisen luvun ensimmäiselle, toiselle, jne numerolle ja ratkaise tehtävä tuloperiaatteen mukaisesti.
eli
Jos samaa numeroa voi käyttää useasti on ensimmäiseen lukuun neljä vaihtoehtoa samoin kuin toiseen ja kolmanteen. Jos samaa lukua ei saa käyttää uudestaan on ensimmäiseen lukuun neljä vaihtoehtoa toiseen lukuun 3 ja kolmanteen 2 vaihtoehtoa. Tehtävän annossa ei tätä mainita, joten tehtävän voi ymmärtäää molemmilla tavoilla.
13 a) Pohdi, kuinka monta vaihtoehtoa on ensimmäiselle, toiselle, jne nostolle, kun pallo palautetaan aina takaisin pöydälle. Ratkaise tehtävä tuloperiaatteen mukaisesti.
b) Nyt pallo jätetään palauttamatta, mikä vaikuttaa ensimmäisen noston jälkeisiin vaihtoehtojen lukumääriin. Pohdi, kuinka monta vaihtoehtoa on ensimmäiselle, toiselle, jne nostolle, kun pallo palautetaan aina takaisin pöydälle. Ratkaise tehtävä tuloperiaatteen mukaisesti.
s.95 t15, jos minulla on 1 karkki ja sinulla 2 karkkia, niin sinulla on kaksi kertaa enemmän karkkeja. Sama pätee todennäköisyyslaskuissa. Eli 2/8=0,25=25% on kaksi kertaa enemmän kuin 1/8=0,125=12,5%, joten se on myös kaksi kertaa todennäköisempää saada jompi kumpi kahdesta radasta.
