3.3

359

$\frac{a}{b}=\frac{x}{y}$
$\frac{356}{558}=\frac{x}{762-x}$
$558x=271272-356x$
$914x=271272\ \parallel:914$
$x=296.79...m\approx297m$

$y=762m-x\approx465m$

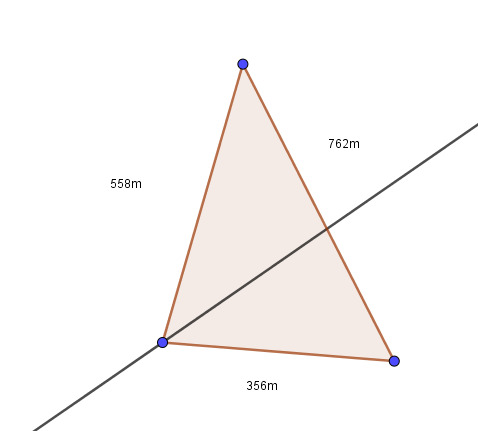
ratkaistaan 558m pitkän sivun vastainen kulma ennen puolitusta kosinilauseella, jotta voidaan laskea pienemmän kolmion pinta-ala $A=\frac{1}{2}ab\sin\gamma$

$c^2=a^2+b^2-2ab\cos\gamma$
$558^2=356^2+762^2-2\cdot356\cdot762\cdot\cos\gamma$
$-396016=-542544\cdot\cos\gamma\ \parallel:\left(-542544\right)$
$\cos\gamma=43.119...°\approx43°$
$A_{pienempi\ kolmio}=\frac{1}{2}\cdot356m\cdot297m\cdot\sin43{,}119...$
$=36135.39...m^2\approx36135m$

ratkaistaan 356m pitkän sivun vastainen kulma ennen puolitusta kosinilauseella, jotta voidaan laskea suuremman kolmion pinta-ala $A=\frac{1}{2}ab\sin\gamma$
$c^2=a^2+b^2-2ab\cos\gamma$
$356m^2=558m^2+762m^2-2\cdot558\cdot762\cdot\cos\gamma$
$850392\cos\gamma=-765272\ \parallel:850392$
$\gamma=154{,}1455...°$
$A=\frac{1}{2}ab\sin\gamma$

$A=56575.61...m^2\approx56576m^2$

nyt lasketaan kuinka monta prosenttia pienemmän kolmion pinta-ala on suuremman pinta-alasta

$\frac{36135m^2}{56576m^2}=0{,}63870...\approx63{,}9\%$

V: 64%

348

a) Jana AC on kolmion keskijana, muiden keskijanojen kanssa se leikkaa pisteessä B
Keskijanojen suhde leikkauspisteen kanssa kärjestä lukien on 2:1
Janojen AC ja BC suhde on siis 2+1:1=3:1
b)
keskijana AC jakaa kolmion kahteen yhtäsuureen kolmioon
toinen niistä on suorakulmainen kolmio, jonka hypotenuusa AC on.
Janan AC pituus voidaan laskea Pythagoraan lauseella
$a^2+b^2=c^2$
$6^2+4^2=c^2$
$52=c^2$
$AC=c\approx7{,}21$
janan BC pituus saadaan jakamalla AC pituus kolmella
$BC=\frac{AC}{3}\approx2{,}40$