MAA5 (MImm)
Kokeen palautus tähän. Huom! Sulkeutuu kello 12.00
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
26.5. KOE klo 8-12
14.5. - Kurssin loppuosan itsearvionti
tehtävän 336 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
13.5. - Paraabeli
Samalla tavoin kuin ylös- tai alaspäinaukeaville paraabeleille voidaan oikealle tai vasemmalle aukeaville paraabeleille johtaa
huippumuoto x-x0 = a(y – y0)2
ja yleinen muoto x = ay2 + by + c
Huom! Jos a>0, aukeaa paraabeli oikealle ja jos a<0 vasemmalle.
Jos paraabelin aukeamissuunta tunnetaan, kolme pistettä määrää paraabelin yksikäsitteisesti, eli kolmen pisteen kautta voidaan piirtää vain yksi paraabeli.
Esim.

Huom! Muotoa y = ax2 olevien paraabelien polttopiste on (0,1/4a) ja johtosuora y = -1/4a, sekä muotoa x = ay2 paraabelien polttopiste (1/4a, 0) ja johtosuora x = -1/4a.
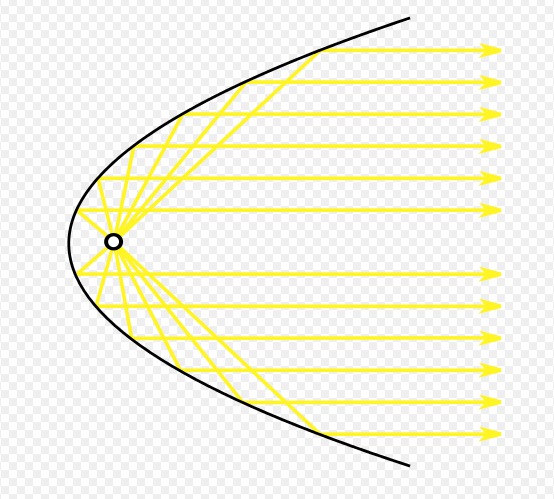
Paraabelista rakennetta voi hyödyntää vaikkapa valonheittimissä jossa säteiden halutaan lähtevän polttopisteestä tiettyyn suuntaan tai lautasantennissa jossa saapuvien säteiden halutaan kokoontuvan polttopisteeseen.
Harjoituksia 336 (palautettava), 347
Halutessaan voi syventää tutkimalla viistoon aukeavia paraabeleja: 354
tehtävän 334 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
11.5.2020 - Paraabeli
Paraabeli on niiden pisteiden ura, jotka ovat yhtä kaukana polttopisteestä ja johtosuorasta.
Aloitetaan käymällä esimerkkinä kirjan tehtävä 341.


Yleisesti ylös tai alaspäin aukeavalle paraabelille voidaan johtaa yhtälö

Josta poistamalla sulut saadaan muoto

Huom! Jos a>0 aukeaa paraabeli ylöspäin ja jos a<0 aukeaa paraabeli alaspäin.
Huippumuoto on kätevä jos tunnetaan paraabelin huippu ja piste jonka kautta se kulkee.
Esim.

Harjoituksia 327, 334 (palautettava)
matikkamatskut: https://www.youtube.com/watch?v=UeblkbLsil8&feature=emb_logo
tehtävän 309 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
7.5.2020 - Tangentin määrittäminen






matikkamatskut: https://www.youtube.com/watch?v=g-invNf2bZA&feature=emb_logo
Harjoituksia 307, 309 (palautettava)
syventäviä 310, 323
tehtävän 280 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
6.5.2020 - Leikkauspisteitä

Ympyrän ja suoran tai kahden ympyrän leikkauspisteitä ratkaistaessa muodostuu epälineaarinen yhtälöpari. Se siis tarkoittaa että ainakin toisessa yhtälössä muuttujan potenssi on jotain muuta kuin ykkönen. Tällaisen yhtälöparin ratkaiseminen ei aina ole helppoa (ellei käytä laskinta). Jos toinen yhtälö on lineaarinen (suoran yhtälö) kannattaa käyttää sijoitus keinoa ratkaisemalla toinen muuttujista lineaarisesta osasta ja sijoittaa se sitten toiseen yhtälöistä. Jos molemmat osat ovat epälineaarisia voi yrittää eliminoida epälineaarisen osan pois. Alla kirjan esimerkit molemmista tapauksista.




Harjoituksia kaikille jotka kannattaisi ratkaista käsin 280 (palautettava), 285
syventäviä harjoituksia edistyneemmille jotka kannattaisi ratkaista laskimella 299, 301
matikkamatskut: https://www.youtube.com/watch?v=qlO44gCQ_oQ&feature=emb_logo
tehtävän 265 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
4.5.2020 - Ympyrän yhtälön yleinen muoto


Laskimessa on kyllä valmiina komento CompleteSquare joka tekee tuon siirtymän yleisestä muodosta keskipistemuotoon, sitä siis kannattaa tietysti käyttää aina kokeissa jos mahdollista mutta jos yrittää ymmärtää mitä tapahtuu niin käsinhän se on käytävä läpi.
Esim.

Esim. Kolme pistettä määrää ympyrän yksikäsitteisesti. Toisin sanoen kolmen pisteen kautta voidaan piirtää vain yksi ympyrä. Yhtälön näistä saa seuraavasti

Harjoituksia:
kaikille 259, 265 (palautettava)
syventyville 270
matikkamatskut: https://www.youtube.com/watch?v=q2bWXRH8Vj4&feature=emb_logo
tehtävän 246 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
30.4.2020 - Ympyrän yhtälön keskipistemuoto
Määritetään pisteen (x,y) etäisyys r pisteestä (x0,y0).
Pythagoraan lausetta käyttämällä saadaan lauseke
Yhtälön toteuttavat kaikki pisteet (x,y) jotka ovat r:n etäisyydellä pisteestä (x0,y0). Saatiin ympyrän yhtälö
Esimerkkinä


Harjoituksia vapun ratoksi, palautus tämän viikon loppuun mennessä.
242, 245 (palautettava), 246
matikkamatskut: https://www.youtube.com/watch?v=bpcb4eGEeGg&feature=emb_logo
Tehtävän 211 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
29.4.2020 - Lineaarinen yhtälöryhmä

Geometrisesti tulkittuna:

Kolmen muuttujan yhtälö voidaan tulkita geometrisesti tason yhtälöksi ja kolmen yhtälön ryhmä kolmen tason leikkauspisteen määrittämiseksi. Kolme tasoa voi leikata toisensa yhdessä pisteessä, pitkin suoraa tai ne voivat olla kolme päällekkäistä tasoa niin että kaikki pisteet ovat yhteisiä tai niin että näillä ei ole yhteisiä pisteitä lainkaan. Vastaus pitää osata tulkita ymmärtäen mistä näistä tapauksista on kysymys.
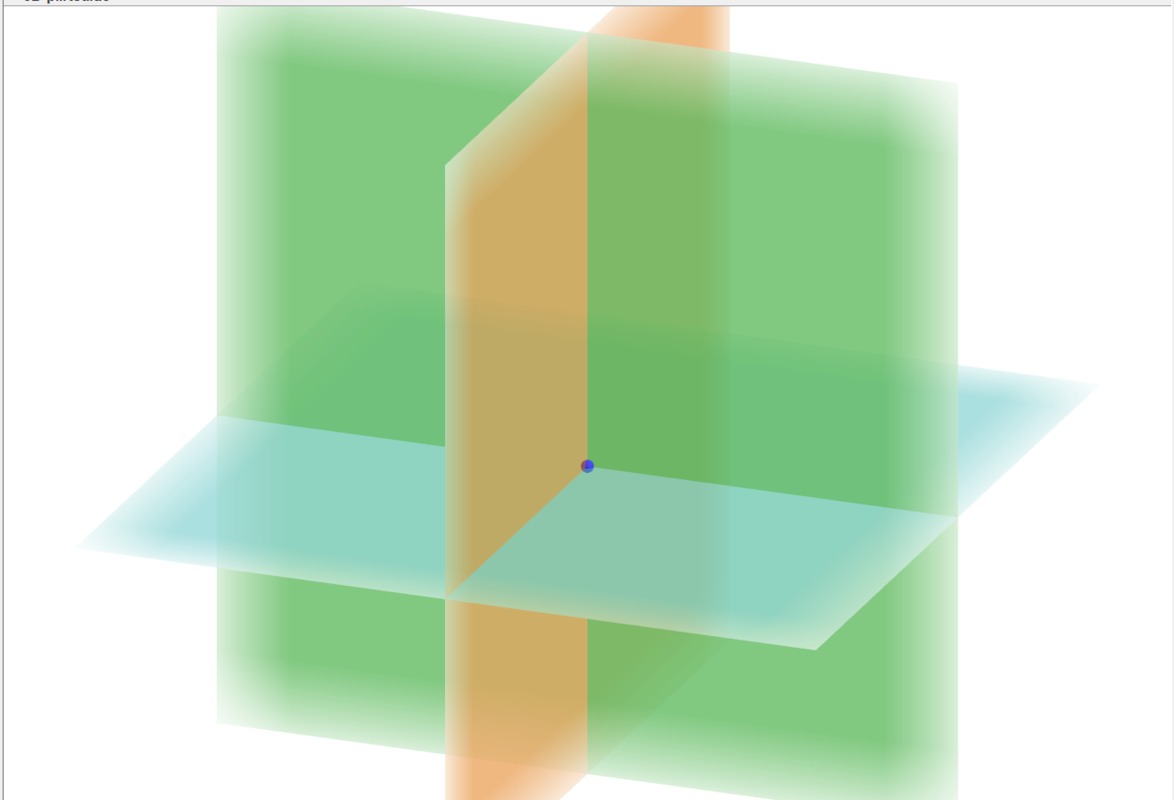


Esimerkkinä otetaan 222. Tällaiset menee käsin ratkaistaessa väkisin hieman pitkiksi.


Eli yksi yhteinen piste (3, -1, -2) saatiin. Näitä kannattaa ehkä piirrellä geogebralla niin auttaa hahmottamaan tilannetta ja tulkitsemaan vastausta. Varsinkin jos vastaukseksi saadaan suoran yhtälö niin voi tuntua aluksi hämärälle.
Harjoituksia 211 (palautettava) ja 224 (Kun on kolme muuttujaa ja kaksi yhtälöä voit ratkaista kaksi muuttujista kolmannen suhteen. Ohje: Eliminoi ensin yhtälöparista yksi muuttujista ja ratkaise saamastasi yhtälöstä toinen jäljelle jäänyt. Sitten eliminoi yhtälöparista äsken ratkaisemasi muuttuja ja saamastasi yhtälöstä ratkaise ensimäiseksi eliminoimasi muuttuja. Jos sait ratkaisun voidaan tulkita geometrisesti että kaksi tasoa leikkaa, jos et saanut ratkaisua kaksi tasoa ei leikkaa. Geogebra auttaa hahmottamaan millainen muoto leikkauskuvio on. Huomaa että vastaus voi olla erinäköinen kuin kirjan takana riippuen mitkä muuttujat olet ratkaissut.)
tehtävän 210 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
27.4.2020 - Lineaarinen yhtälöryhmä

Huom! Geometrisesti tulkittuna tämä tarkoittaa kahden suoran leikkauspisteen etsimistä. Yhtälöparin yhtälöthän ovat molemmat suoran yhtälöitä.


Huom! Geometrisesti tulkittuna se että suorilla on äärettömän paljon yhteisiä pisteitä tarkoittaa että ne kulkevat päällekkäin ja yhtälöparin ratkaisuksi käyvät kaikki suoran pisteet.

Mieti vielä mitä tarkoittaa jos saat ratkaisuksi että yhtälö on identtisesti epätosi.

Laskimella kannattaa olla tarkka mille riville ja minkä sulun sisään ratkaistavat muuttujat tulevat. Varmista että osaat käyttää laskinta.
Huom! Käsin kun ratkaiset murtolukukertoimisia yhtälöitä tai yhtälöryhmiä saattaa olla hyvä tehdä "ylimääräinen" välivaihe jossa kaikki yhtälöt kerrotaan sellaisilla luvuilla että kertoimet muuttuvat kokonaisluvuiksi.
Harjoituksia (käsin nämä tee!) 208, 210 (palautettava)
syventävä tehtävä 226
matikkamatskut: https://www.youtube.com/watch?v=xNkAKUq-cqs&feature=emb_logo
23.4.2020 - Puolivälin arviointi
tehtävän 185 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
22.4.2020 - Pisteen etäisyys suorasta
Pisteen (x0,y0) etäisyys suorasta ax + by + c = 0 saadaan kaavalla
Kaavan johtaminen on hieman pitkä. Sen voi tarkistaa kirjasta. Tärkeintä nyt olisi opetella käyttämään sitä eri tilanteissa. Huomaa, että
x0 on suoran ulkopuolisen pisteen x koordinaatti
y0 on suoran ulkopuolisen pisteen y koordinaatti
a on x:n kerroin suoran yhtälöstä kun se on yleisessä muodossa.
b on y:n kerroin suoran yhtälöstä kun se on yleisessä muodossa.
c on vakio-osa suoran yhtälön yleisestä muodosta.
Tutki seuraavat kirjan tehtävät läpi esimerkkeinä





matikkamatskut: https://www.youtube.com/watch?v=G3JUz0nJi1M&feature=emb_logo
Harjoituksia 183, 185 (palautettava), 191
ja sitten oikeestaan ois hyvä vielä tehdä 189, 202 mutta nää niille jotka haluaa sen kiitettävän osaamisen.
tehtävän 162 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
20.4.2020 - Kohtisuorat suorat
Suorat ovat kohtisuorassa toisiaan vastaan jos niiden kulmakertoimien tulo k1k2 = -1.
Tällöin suoria sanotaan toistensa normaaleiksi.

Janan keskinormaalilla tarkoitetaan janaa vastaan kohtisuorassa olevaa suoraa joka kulkee janan keskipisteen kautta. Keskinormaalin pisteet ovat yhtä kaukana janan päätepisteistä.
Esimerkkeinä kannattaa lukaista kirjan tehtävät 156 ja 170



matikkamatskut: https://www.youtube.com/watch?v=LHKXzVxJBlQ&feature=emb_logo
Harjoituksina:
157, 159, 162 (palautettava), 164
tehtävän 135 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
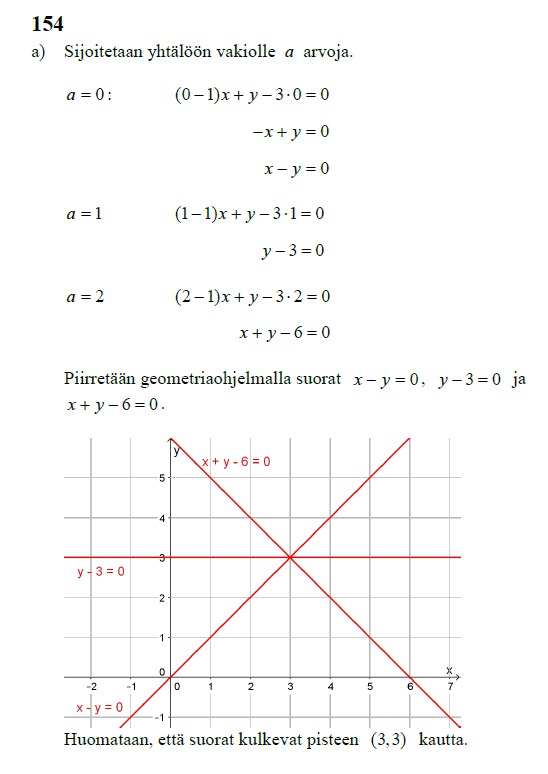
16.4.2020 - Suoran yhtälö

Huom! Suoran yhtälöä varten tarvitset siis yhden pisteen (x0, y0) ja kulma kertoimen k tai vaihtoehtoisesti kaksi pistettä joiden avulla voit laskea kulmakertoimen ja sitten valitset toisen pisteistä pisteeksi (x0,y0). Sitten vaan y-y0 = k (x-x0).





Tietokoneella suoran piirtäminen käy helposti geogebralla johon suoran yhtälön voi syöttää suoraan missä muodossa tahansa. Laskinohjelmassa jotuu taas vähän valikoita selaamaan.
147b.



matikkamatskut: https://www.youtube.com/watch?v=Nm1V2-5dHCY&feature=emb_logo
Harjoituksia 133, 135 (palautettava), 137, 138, 140
Hyviä syventäviä tehtäviä niille joilla aikaa riittää 149, 153
tehtävän 116 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
15.4.2020 - Suoran kulmakerroin

Esim.
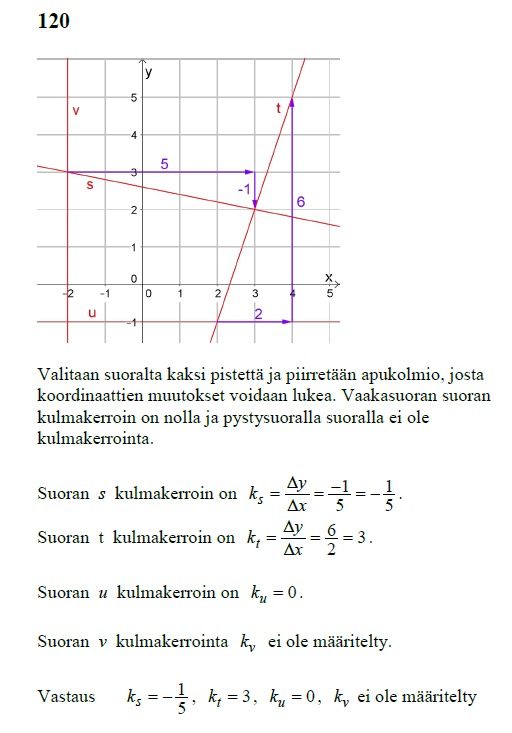
Esim. 124

matikkamatskut:
https://www.youtube.com/watch?v=1dmre2rLG1k&feature=emb_logo
Palautettavana tehtävänä sitten harjoitellaan vähän geogebraa tai laskimen piirto-ominaisuuksia.
Harjoituksia 110, 112, 114, 116 (palautettava), 118, 125
niille jotka haluaa vielä vähän ekstraa voisivat kokeilla vaativampana harjoituksena 128
tehtävän 97 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
9.4.2020 - Tason koordinaatisto ja pistejoukon yhtälö
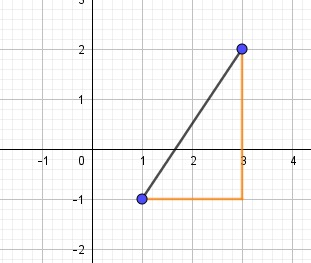
Esim. Laske pisteiden (3,2) ja (1, -1) välinen etäisyys.
Vastaavasti pisteiden (x1,y1) ja (x2,y2) välinen etäisyys saadaan
Janan keskipisteen koordinaatit saadaan x- ja y-koordinaattien keskiarvona päätepisteiden koordinaateista.
Esimerkkinä kirjasta

Kolmio on suorakulmainen jos sivujen pituudet toteuttavat Pythagoraan lauseen. Huomaa että pisin sivu on se jota kannattaa kokeilla hypotenuusaksi.
Esim.

Analyyttisessä geometriassa kuviot määrätään yhtälöin. Piste on kuvion piste, vain jos sen koordinaatit toteuttavat pistejoukon yhtälön.
Esim.
Piste (1,1) kuuluu suoralle 2y + 3x – 5 = 0, koska 2∙1 + 3∙1 – 5 = 0
Piste (1,2) ei kuulu paraabeliin y = 2x2 + 1, koska 2 ≠2∙12 + 1
Erilaisten pistejoukkojen hahmottamisen voi aloittaa vaikka ratkaisemalla yhtälöstä muuttujan y
Esim.


Yleensä piirtäminen kannattaa ehdä laskimella tai geogebralla. Geogebra on siitä kätevä että tähän voi kuvaajan syöttää suoraan yhtälömuodossa, laskinohjelmassa voi ratkaista y:n ja syöttää funktiona tai sitten pitää tunnistaa mistä muodosta on kysymys
Esim. 107a
matikkamatskuvideot:
https://www.youtube.com/watch?v=NYbtTG-jcLo&feature=emb_logo
https://www.youtube.com/watch?v=0dJiCgYKAXc&feature=emb_logo
Harjoituksia 74, 75, 81, 94, 97 (palautettava)
Tehtävän 56 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
8.4.2020 - Itseisarvoepäyhtälö

kun saat ratkaisuksi lukusuoran alueen joka on kahdessa osassa, tulee vastauskin ilmoittaa kahdella epäyhtälöllä kuten yllä.
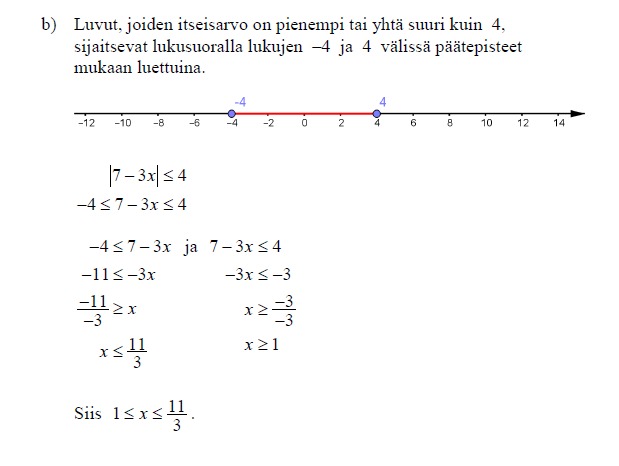
kun saat ratkaisuksi lukusuoran alueen joka on yhdessä osassa voit ilmoittaa vastauksen kaksoisepäyhtälönä tai kahdella eri epäyhtälöllä ja "ja"-sanaa käyttämällä kuten yllä. Tarkkana myös suljetun ja avoimen välin kanssa, eli tuleeko yhtäsuuruus mukaan epäyhtälöön.
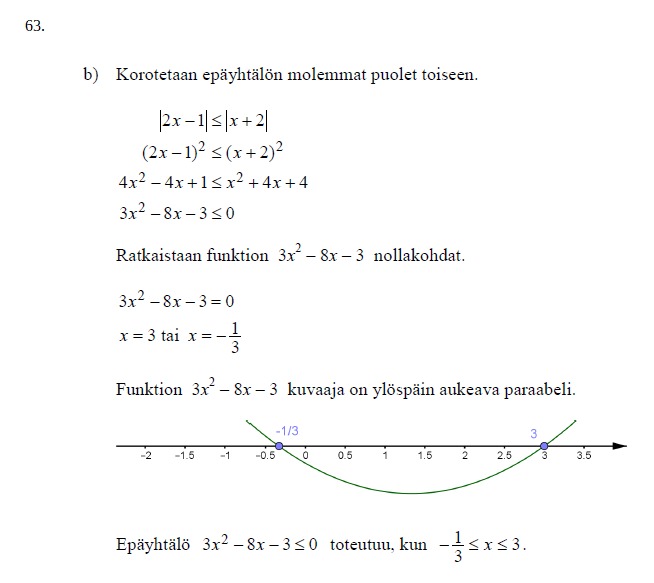
Itseisarvoepäyhtälö voidaan ratkaista myös korottamalla epäyhtälö puolittain toiseen potenssiin (muista neliöön korotusehto!). Koska toinen potenssi on vähintään nollan suuruinen voidaan itseisarvot tämän jälkeen jättää pois. Tosin tässä on tietysti vaara että korottamisen jälkeinen epäyhtälö on vaikea ratkaista esimerkiksi korkean potenssin takia.
matikkamatskut aiheeseen
https://www.youtube.com/watch?v=hN1Czjt44nI&feature=emb_logo
Harjoituksia 49, 51, 54, 56 (palautettava)
tehtävän 32 palautus
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.
6.4.2020 - Itseisarvoyhtälö
Itseisarvo määritellään seuraavasti

Geometrisesti tulkittuna |x| tarkoittaa x:n etäisyyttä origosta.
Vastaavasti |a – b| tarkoittaa a:n ja b:n etäisyyttä lukusuoralla.
Tutkitaan seuraavaksi lauseketta |ab| eri tapauksissa.
-
Olkoon a<0 ja b<0. Nyt |ab|= ab = |a||b|
-
Olkoon a<0 ja b≥0. Nyt |ab|= -ab = |a||b|
-
Olkoon a≥0 ja b≥0 Nyt |ab| = ab = |a||b|
Siis |ab|=|a||b| ja vastaavasti voidaan johtaa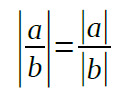
Huom! Määritelmästä seuraa |a|=|-a|.
Käy seuraavaksi läpi seuraavat tehtävät
Matikkamatskut on tehnyt myös hyvää videota aiheeseen
https://www.youtube.com/watch?v=ugqbkbOtS_M&feature=emb_logo
https://www.youtube.com/watch?v=RSJvJVZwbqg&feature=emb_logo
Harjoituksia 12, 13, 14, 15, 29, 32 (palautettava), 41