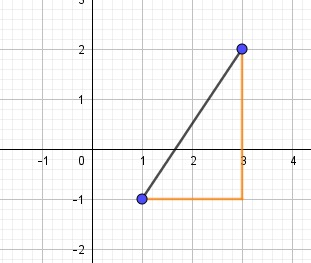
Esim. Laske pisteiden (3,2) ja (1, -1) välinen etäisyys.

Pythagoraan lauseella saadaan

Vastaavasti pisteiden (x₁,y₁) ja (x₂,y₂) välinen etäisyys saadaan

Janan keskipisteen koordinaatit saadaan x- ja y-koordinaattien keskiarvona päätepisteiden koordinaateista.
Esimerkkinä kirjasta

Kolmio on suorakulmainen jos sivujen pituudet toteuttavat Pythagoraan lauseen. Huomaa että pisin sivu on se jota kannattaa kokeilla hypotenuusaksi.
Esim.

Analyyttisessä geometriassa kuviot määrätään yhtälöin. Piste on kuvion piste, vain jos sen koordinaatit toteuttavat pistejoukon yhtälön.

Esim.

Piste (1,1) kuuluu suoralle 2y + 3x – 5 = 0, koska 2∙1 + 3∙1 – 5 = 0

Piste (1,2) ei kuulu paraabeliin y = 2x² + 1, koska 2 ≠2∙1² + 1

Erilaisten pistejoukkojen hahmottamisen voi aloittaa vaikka ratkaisemalla yhtälöstä muuttujan y
Esim.


Yleensä piirtäminen kannattaa ehdä laskimella tai geogebralla. Geogebra on siitä kätevä että tähän voi kuvaajan syöttää suoraan yhtälömuodossa, laskinohjelmassa voi ratkaista y:n ja syöttää funktiona tai sitten pitää tunnistaa mistä muodosta on kysymys
Esim. 107a

matikkamatskuvideot:
https://www.youtube.com/watch?v=NYbtTG-jcLo&feature=emb_logo
https://www.youtube.com/watch?v=0dJiCgYKAXc&feature=emb_logo

Harjoituksia 74, 75, 81, 94, 97 (palautettava)