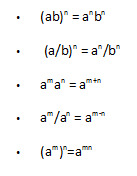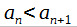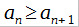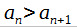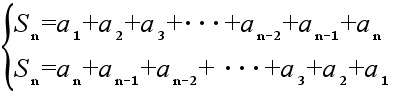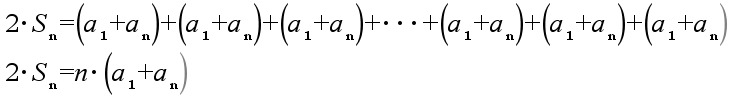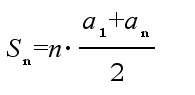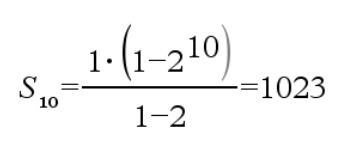MAY1 (MImm)

Luvut ja lukujonot

- Välitestit 2*6p=12p

- Loppukoe 6*12p=72p

- Kokeessa A osio ilman laskinta

- B-Osiossa laskinohjemistot käytössä

- Koe tehdään omalla tietokoneella, usb-tikulta käynnistettävässä Abitti-ympäristössä

- Laskimena käytetään TI-nspire -ohjelmistoa. Nspire.fi/aloitus

- Toinen ohjelmisto Geogebra. Geogebra.org

- Kirjana Sanomapro: Tekijä

- Taulukkokirjana Otava: MAOL-taulukot

1 - Kokonaisluvut

Lukujoukot:

Luonnolliset luvut

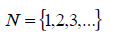
Kokonaisluvut

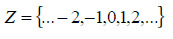
Rationaaliluvut

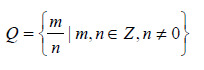
Irrationaaliluvut ovat niitä reaalilukuja, jotka eivät ole rationaalilukuja. Ne tunnistaa päättymättömästä, jaksottomasta desimaaliesityksestä.


Reaaliluvut R on edellisten yhdiste


Reaalilukujen laskutoimitukset (yhteenlasku ja kertolasku) ovat vaihdannaisia ja liitännäisiä

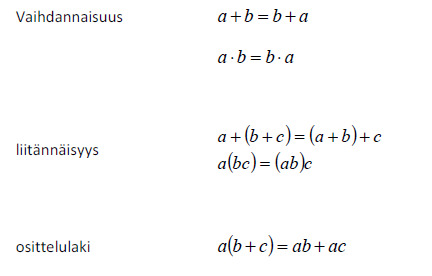
Esimerkki 11.

Luvun ja sen vastaluvun summa on nolla.



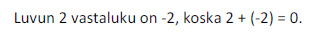
Itseisarvo ilmaisee luvun etäisyyden lukusuoralla luvusta nolla. Luku ja sen vastaluku ovat lukusuoralla yhtä kaukana luvusta nolla.

Esimerkki 17

Harjoituksia 1, 4, 6, 8, 10, 12 + 18, 20


2 - Reaaliluvut

Luvun ja sen käänteisluvun tulo on yksi

Murtolukujen summa lasketaan

  • Lavenna saman nimisiksi
  • Laske osoittajat yhteen

Murtolukujen tulo lasketaan

  • Supista jos mahdollista
  • Kerro osoittajat ja nimittäjät keskenään

Sekaluvut kannattaa muuttaa usein murtoluku muotoon

Esimerkki 30

Esimerkki 33

Esimerkki 41

Harjoituksia 26, 27, 29, 32, 34, 35 + 42, 43

3 - Yhtälö ja epäyhtälö

Kun kaksi lauseketta merkitään yhtä suuriksi, saadaan yhtälö. Tämä voi olla tosi tai epätosi. Muuttujan arvoja, joilla yhtälö on tosi sanotaan yhtälön ratkaisuiksi, eli juuriksi.

Esimerkki 45

Esimerkki 48

Esimerkki 52

Epäyhtälössä ratkaisu keinot ovat samat kunhan muistaa kääntää epäyhtälön suunnan kerrottaessa tai jaettaessa negatiivisella luvulla.

Esimerkki 55

Harjoituksia 46, 51, 54, 58, 60, 61, 62

4 - Potenssi


Esimerkki 67

Esimerkki 74

Esimerkki 77

Esimerkki 78

Esimerkki 85

Harjoituksia 68, 69, 70, 73, 75, 86, 88

6 - Eksponentin ratkaiseminen

Yhtälö jossa muuttuja esiintyy eksponentissa, voidaan ratkaista

  • Muuttamalla lausekkeiden kantaluvut yhtä suuriksi
  • Käyttämällä apuna logaritmia

Esimerkki 116

Esimerkki 119

Luvun b a-kantainen logaritmi tarkoittaa yhtälön ax = b ratkaisua.

Esimerkki 125

Esimerkki 128

Harjoituksia 115, 120, 123, 124, 126, 133

7 - Prosenttilaskentaa

Prosentti tarkoittaa sadasosaa, eli

1% = 1/100 = 0,01

Huom! Promille 1‰ = 1/1000



Esimerkki 139

Esimerkki 164

Esimerkki 167

Harjoituksia 142, 145, 148, 149, 152, 168, 170

8 - Prosentuaalinen muutos

Muutos voidaan ilmaista myös prosenttiyksikköinä.

Esimerkiksi jos lainan korko nousee yhden prosenttiyksikön 2 prosentista 3 prosenttiin on muutos yhden prosenttiyksikön mutta muutoksen suuruus prosentteina on (3-2)/2 * 100% = 50%.

Esimerkki 154


Prosenttiyhtälöt voidaan ratkaista lausekkeen

prosenttikerroin x alkuarvo = loppuarvo

Esimerkki 171

Esimerkki 175

Harjoituksia 153, 157, 172, 173, 176

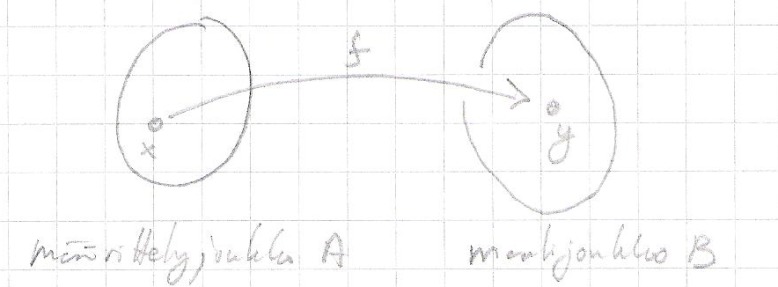
9 - Funktio

Funktio joukosta A joukkoon B on sääntö, joka liittää jokaiseen joukon A alkioon yhden alkion joukosta B.



Merkitään f: A->B

Esim.

Ympyrän pinta-ala riippuu sen säteestä, joten ympyrän pinta-ala on säteen funktio ja sääntö voidaan esittää vaikkapa muodossa A(r) = πr2.


Esimerkki 186

Esimerkki 190

Esimerkki 193

Esimerkki 201

Harjoituksia 185, 192, 195, 200, 202

10 - Funktion kuvaaja

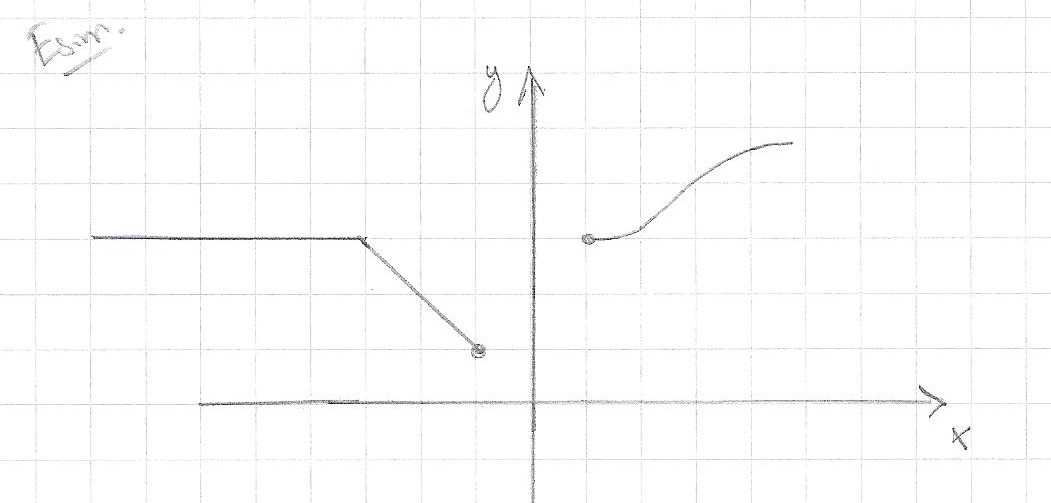
Olkoon y x:n funktion, eli y = f(x). Funktion arvoa eri muuttujan arvoilla voidaan havainnollistaa kuvaajan avulla.

Esim.

Nyt

  • f(-5) = 3
  • f(-4) = 3
  • f(-2) = 2
  • f(3) = 4

Huom! Funktiota ei ole määritelty kun -1 < x < 1.

Esimerkki 208

Esimerkki 211

Esimerkki 218 Kuvaajan piirtäminen käsin

Esimerkki 217 Kuvaajan piirtäminen laskimella

Harjoituksia 206, 210, 214, 220, 224, 225

11 - Lukujono

Määritteleminen yleisen jäsenen avulla:

lukujonon jäsenet a1, a2, a3, … , an, … missä on positiivinen kokonaisluku, ilmaistaan yleisen jäsenen an avulla.

Esim.
an = 2n – 1 määrittelee jonon 1, 3, 5, 7, …

an = 1/n määrittelee jonon 1, ½, 1/3, …


Lukujono (an) on

kasvava, kun

aidosti kasvava, kun

vähenevä, kun

aidosti vähenevä, kun

monotoninen = kasvava tai vähenevä

 

Esim.

Olkoon an = n + (n-1)(n-2)(n-3)(n-4)*(π-5)/24

nyt

a1 = 1

a2 = 2

a3 = 3

a4 = 4

a5 = 5+π

Esimerkki 231

Esimerkki 234

Esimerkki 237

Harjoituksia 230, 233, 235, 236, 241, 243

11 - Rekursiivinen lukujono

Rekursiivisesti määritelty jono:

Seuraava jäsen ilmoitetaan edellisten avulla.

Esim. Fibonaccin jono

Jono on 1, 1, 2, 3, 5, 8, 13, …

Esimerkki 250

Esimerkki 258

Esimerkki 259

Harjoituksia 249, 252, 256, 260, 261, 264

12 - Aritmeettinen lukujono

Lukujonoa sanotaan aritmeettiseksi jos sen peräkkäisten jäsenten erotus (differenssi) on vakio.

Esim.

Jono 1,2,3,4,5,… d=1

tai jono 4, 2, 0, -2, -4, … d=-2


Esim. Selvitä aritmeettisen lukujonon 6, 10, 14, … n. jäsen.

Differenssi d saadaan peräkkäisten jäsenten erotuksena 10 – 6 = 4.

a1 = 6

a2 = 6 + 4

a3 = (6 + 4) + 4 = 6 + 2x4

a4 = (6 + 2x4) + 4 = 6 + 3x4

…

an = 6 + (n -1)x4

Huom! Aritmeettisen lukujonon yleinen jäsen an = a1 + (n-1) x d

Esimerkki 269

Esimerkki 272

Esimerkki 273

Esimerkki 277

Esimerkki 284

Harjoituksia 268, 271, 276, 278, 283, 287

13 - Aritmeettinen summa

Lasketaan aritmeettisen lukujonon n ensimmäistä jäsentä yhteen ja kirjoitetaan saatu summalauseke kahdella tavalla.

Josta saadaan

ja edelleen laskemalla lausekkeet puolittain yhteen

Jaetaan lopuksi saatu yhtälö puolittain kahdella jolloin saamme aritmeettisen summan lausekkeeksi:

Esimerkki

Laske 1+2+3+...+99+100.

Summa saadaan

Esimerkki 293

Esimerkki 297

Esimerkki 300, 301 (Summamerkintä)

Esimerkki 302

Harjoituksia 291, 296, 300, 301, 303, 310

14 - Geometrinen lukujono

Lukujonoa sanotaan geometriseksi jos sen peräkkäisten jäsenten suhde on vakio.

Esimerkki

Jono 1, 2, 4, 8, 16, … suhdeluku q=2

jono -1, 1, -1, 1, -1, … q=-1

 

Esimerkki: Selvitä geometrisen lukujonon 1, 2, 4, 8, … n. jäsen.

Suhdeluku saadaan peräkkäisten jäsenten suhteena

Jolloin

a1 = 1

a2 = 1 x 2

a3 = (1 x 2) x 2 = 1 x22

a4 = (1 x22) x 2 = 1 x23

a5 = (1 x23) x 2 = 1 x24

…

an = 1 x2n-1


Huom! Geometrisen jonon yleinen jäsen an = a1 x qn-1


Esimerkki 315

Esimerkki 318

Esimerkki 320

Harjoituksia 317, 321, 322, 325, 326 + 330

15 - Geometrinen summa

Kirjoitetaan ensin summa lausekkeet joista ensimmäisessä on laskettu yhteen n kappaletta geometrisen lukujonon jäseniä ja jälkimmäisessä sama summa on kerrottu luvulla q.

Vähennetään ylemmästä lausekkeesta puolittain alempi, jolloin saadaan

Tästä ottamalla yhteinen tekijä, yhtälö saa muodon

Josta edelleen jakamalla puolittain termillä 1 – q, saadaan geometrisen summan lauseke

Esimerkki

Laske summa 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512.

Esimerkki 340

Esimerkki 343

Esimerkki 345

Harjoituksia 339, 341, 342, 344, 348, 354