Sinin ja kosinin määritelmä

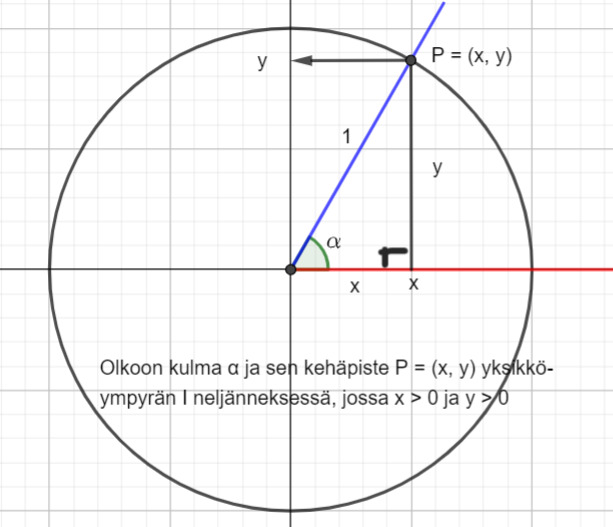
Kulman α sini ja kosini voidaan määritellä kuvan suorakulmaisen kolmion avulla, jossa kateetit ovat x ja y sekä hypotenuusa 1 (ympyrän säde).

$\sin\alpha=\frac{y}{1}=y$

eli kulman sini on kulmaa vastaavan kehäpisteen y-koordinaatti
$\cos\alpha=\frac{x}{1}=x$

eli kulman kosini on kehäpisteen x-koordinaatti

Tämä on voimassa kaikille kulmille α

$Nyt\ voidaan\ merkitä:\ kulman\ \alpha\ kehäpiste\ P\ =\ \left(x{,}\ y\right)=\left(\cos\alpha{,}\ \sin\alpha\right)$

Nyt nähdään yksikköympyrältä helposti, että kulman π kehäpiste (-1, 0).

Tämän perusteella sinπ =0 ja cosπ = -1 (nähdään myös laskimella tai taulukkokirjasta)

$Mikä\ on\ kulman\ 250°\ ja\ \frac{7\pi}{4}\ kehäpiste?$

Sinin ja kosinin etumerkit eri neljänneksissä:

$\sin\alpha\gt 0\ I:ssä\ ja\ II:ssa\ sekä\ \cos\alpha\gt 0\ I:ssä\ ja\ IV:ssa$

$\sin\alpha\lt 0\ III:ssa\ ja\ IV:ssa\ ja\ \cos\alpha\lt 0\ II:ssa\ ja\ III:ssa$

Kotitehtävät: 123, 125 ja 127

Sinin ja kosinin perusominaisuuksia

1. Arvojoukko

$-1\le\sin\alpha\le1\ \ ja\ -1\le\cos\alpha\le1\ eli\$

eli sinin ja kosinin arvojoukko on [-1, 1]

koska yksikköympyrällä kehäpisteen x ja y-koordinaatti on suurimmillaan 1 ja pienimmillään -1

2. Jaksollisuus

Jos kulmaan α lisätään tai vähennetään täysiä kierroksia niin päädytään samaan kehäpisteeseen.

$\sin\left(\alpha\right)=\sin\left(\alpha+n\cdot2\pi\right)=y$

$\cos\left(\alpha\right)=\cos\left(\alpha+n\cdot2\pi\right)=x\ {,}\ n\in\mathbb{Z}\ \left(n\ voi\ olla\ mikä\ tahansa\ kokonaisluku\right)$

Sanotaan, että sinin ja kosinin jaksona on 2π (ovat 2π jaksollisia)

3. Trigonometrian perusyhtälö

Kuvan suorakulmaiselle kolmiolle on voimassa Pythagoraan lause

$x^2+y^2=1{,}\ jossa\ x=\cos\alpha\ ja\ y=\sin\alpha{,}\ joten$

$\left(\cos\alpha\right)^2+\left(\sin\alpha\right)^2=1{,}\ nyt\ merkitään\ \left(\sin\alpha\right)^2=\sin^2\alpha\ ja\ \left(\cos\alpha\right)^2=\cos^2\alpha$
$eli\ Trigonometrian\ perusyhtälö\ on\ \sin^2\alpha+\cos^2\alpha=1\$

Tämä on Pythagoraan lause yksikköympyrällä (ympyrän jokainen kehäpiste toteuttaa yhtälön)

Määritä kulman α kehäpiste, kun

$\alpha=-\frac{2\pi}{3}$

Kulman kehäpiste saadaan, kun määritetään cosα ja sinα. Nyt kehäpiste on III-neljänneksessä, jossa sinα ja cosα ovat negatiivisia.

Nyt saadaan kehäpisteelle tarkka arvo, jolloin käytetään taulukkoa apuna.

Taulukoikossa on tarkat arvot kulmille väliltä 0 - 2π. Jos kulma ei ole tällä välillä niin silloin voidaan käyttää sinin ja kosinin jaksollisuutta eli lisätään tai vähennetään tähän kulmaan 2π tai sen monikertoja.

$-\frac{2\pi}{3}+2\pi=\frac{4\pi}{3}\ eli\ \sin\left(-\frac{\pi}{3}\right)=\sin\left(\frac{4\pi}{3}\right)=-\frac{\sqrt{3}}{2}$

$\cos\left(-\frac{\pi}{3}\right)=\cos\left(\frac{4\pi}{3}\right)=-\frac{1}{2}\ eli\ P=\left(-\frac{1}{2}{,}-\frac{\sqrt{3}}{2}\right)$

Jos kulma on yli 2π niin silloin voidaan vähentää 2π tai sen monikertoja

Huom!

Voidaan ajatella myös seuraavasti:

$\alpha=\frac{21\pi}{4}=5\pi+\frac{1}{4}\pi=\frac{5\pi}{4}+2\cdot2\pi$
$nyt\ kulmalla\ \alpha\ on\ sama\ kehäpiste\ kuin\ kulmalla\ \frac{5\pi}{4}$

Kotitehtävät: 137, 140 ja 142