Tilastokuvio tarkoittaa jonkin tilastollisen jakauman esittämistä kuvallisesti, jonkin kuvion eli diagrammin avulla.

Jakauma voi olla

• absoluuttinen, eli on laskettu lukumäärät
• suhteellinen, eli lasketaan osuudet

Esimerkki

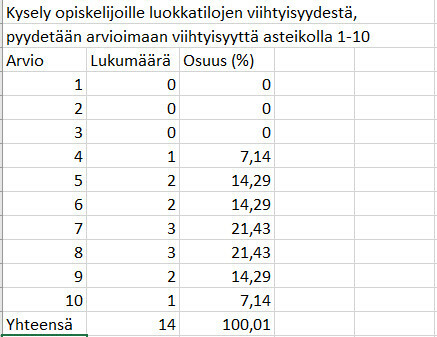
Kyselyssä vastasi 14 opiskelijaa, huomaa, että suhteellisten osuuksien summa on yli 100 %, mikä johtuu pyöristyksestä.

Tässä kyselyssä perusjoukko olisi kaikki opiskelijat ja otanta, (eli otos) on ne opiskelijat, jotka valittiin vastaamaan kyselyyn. Toinen mahdollisuus olisi ollut kysyä kaikilta opiskelijoilta.

Suurissa perusjoukoissa otantatutkimus on ainoa järkevä tapa tehdä nopeita tutkimuksia. Esim. vaaleissa tutkimuksia eli gallupeja tehdään tyypillisesti 1000 – 2000 henkilölle koko Suomessa. (Itse vaalit järjestetään luonnollisesti kaikille.)

Tutkimuksen tuloksiin voi vaikuttaa vahingossa tai tahallisesti se, jos otanta tehdään valikoivasti.

• kello 10 torilla tehtävään kyselyyn valikoituu vähän työssäkäyviä ja koululaisia
• netissä tehtävään kyselyyn valikoituu paljon nuoria
• Helsingissä tehtävään kyselyyn valikoituu paljon kaupunkilaisia

Jakaumia käsitellään joko erityisesti siihen tarkoitetuilla tilastointiohjelmilla tai taulukkolaskentaohjelmilla. Abitissa oleva taulukkolaskentaohjelma on nimeltään Libre Office Calc

Tilastokuvioita on eri tyyppisiä, yleisimmät ovat:

• pylväs
• ympyrä
• viiva
• palkki

Alla olevassa kuvassa on esimerkin kyselyn jakaumat esitetty pylväs ja ympyrädiagrammin avulla

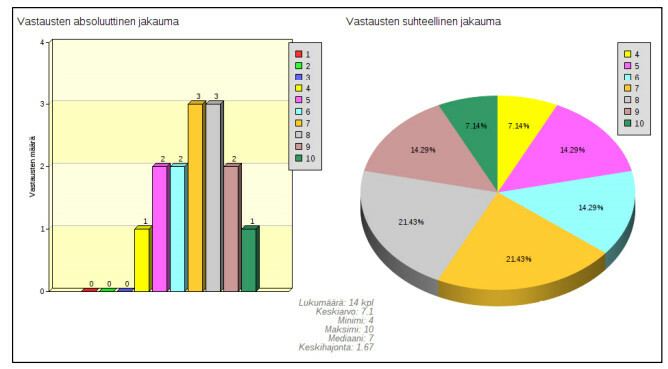
Vasemmalla absoluuttinen jakauma, oikealla suhteellinen jakauma.

Myös diagrammien esittämisellä voidaan tarkoituksella vääristää jakauman tuloksia

• asteikon valinta
• asteikon alkukohta
• värit

Tämän vuoksi diagrammeja lukiessa on olennaista päätellä myös luvut, eikä pelkkää pinta-alan / korkeuden havainnollistusta.

Tunnusluvut

Jakaumien tai otoksien kuviollisen esittämisen lisäksi niille ilmoitetaan usein myös erilaisia tunnuslukuja. Keskiarvo on näistä yleisin, lisäksi:

• keskiarvo
• moodi, eli tyyppiarvo, (siis arvo, joita aineistossa on eniten)
• mediaani, eli keskimmäinen arvo

Itse jakaumaa kuvataan myös useilla tunnusluvuilla, joita ovat:

• määrä
• pienin ja suurin havaintoarvo
• vaihteluvälin pituus
• keskihajonta
• otoskeskihajonta

Nämä selvitetään nykyään lähes poikkeuksetta ohjelmalla, mutta kaikki voidaan laskea myös käsin.

Keskihajonnan voi laskea kaavalla

Otoskeskihajonnan ainoa ero keskihajontaan on, se että laskukaavan nimittäjässä on 𝑛 − 1 eikä 𝑛. Tämä korjaa vääristymää, joka syntyy, kun ei tiedetä koko perusjoukon keskiarvoa.

(tunnuslukuja on kysytty harvoin pitkän matematiikan yo-kokeessa, lyhyessä sen sijaan useammin. Tähän saattaa olla nyt tulossa muutos)

Kotitehtäviksi: 1.2, 1.4, 1.5,1.12, 1.15, 2.3, 2.8, 2.13, 2.20