9. opetuskerta
Todennäköisyysjakaumat

Todennäköisyysjakauma on käsite, joka kuvaa miten todennäköisyys keskimäärin jakautuu mahdollisten vaihtoehtojen välille.
Jakauma ei kerro siitä, mitä tapahtuu, jos todennäköisyyskoe toteutetaan. Esimerkiksi heitetään noppaa. Jakauma kertoo siitä, kuinka usein kukin vaihtoehto toteutuu, kun koetta toistetaan äärettömän monta kertaa.
Diskreetti todennäköisyysjakauma koskee sellaisen muuttujan jakaumaa, joka voi saada vain tiettyjä erillisiä arvoja. Toisin sanoen erilaisia vaihtoehtoja on aina äärellinen määrä. (esimerkiksi satunnaisesti valittu kokonaisluku ei ole sellainen)
Tällaisen satunnaismuuttujan aikaansaa satunnaisilmiöksi kutsuttu tapahtuma
- kolikko
- arpanoppa
- sekoitettu korttipakka
- rulettipöytä
Satunnaismuuttujan jakaumaa havainnollistetaan usein pistekuviolla

Tämä pistekuvio havainnollistaa todennäköisyyksiä sille, kuinka monta pataa saadaan, kun korttipakasta nostetaan satunnaisesti 3 korttia. Pistetodennäköisyyksien avulla voidaan myös määrittää pistetodennäköisyysfunktio, joka on diskreetti funktio ja sen arvo on kunkin mahdollisen arvon todennäköisyys. (ja mahdottomille arvoille 0)
Satunnaiselle jakaumalle lasketaan vastaavia tunnuslukuja, kuin tilastollisille muuttujille. Keskiarvoa vastaava muuttuja on odotusarvo.

Odotusarvo voi olla myös sellainen, jota ei todellisuudessa voi koskaan saada. Esimerkiksi tavallisen arpanopan odotusarvo on 3,5
Keskihajonta kuvaa sama kuin tilastollisilla muuttujilla, eli sitä kuinka paljon muuttujan arvo keskimäärin poikkeaa keskiarvosta, eli odotusarvosta.
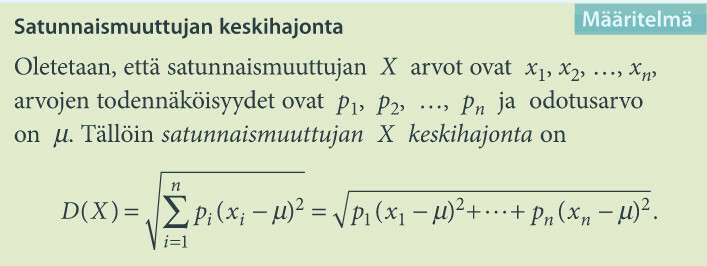
Binomijakauma
Toistokokeen tuottamaa satunnaisuutta kutsuttiin binomitodennäköisyydeksi ja sen tuottamaa jakaumaa kutsutaan binomijakaumaksi.
Binomijakauma on esimerkki diskreetistä jakaumasta, koska se voi saada vain erillisiä arvoja.
Lisäksi binomitodennäköisyydessä vaaditaan, että tapahtuman todennäköisyys on joka kerran sama. (esimerkiksi saadaan nopalla 6, tai saadaan kolikolla klaava.)
Tällöin binomijakaumaan vaikuttaa kaksi parametriä
- tapahtuman todennäköisyys
- toistojen määrä
Usein binomijakauman parametreiksi valitaan n ja p, missä n on toistojen määrä ja p yhden tapahtuman todennäköisyys. Tällöin binomijakaumaa noudattavaa satunnaismuuttujaa X merkitään X ~ Bin (n, p)
Binomijakauman tunnusluvut saadaan seuraavilla kaavoilla.

Binomijakaumalle (kuten useille muille jakaumille) on tyypillistä, että keskimmäisiä arvoja on eniten.
Binomijakaumaa havainnollistetaan usein pylväskaaviolla

Huomaa, että pylväiden summan tulee olla 1.
Laskinohjelmalla saa myös binomijakauman kertymäfunktion, eli sen kuinka suuri todennäköisyys on tietyn valitun rajan ala- tai yläpuolella. Esimerkiksi edellisen kuvan kertymäfunktio P(X>3) = 0,55 mikä saadaan laskemalla kolme ensimmäistä pylvästä yhteen.
Kotitehtäviksi: 229, 230, 238, 245, 249, 255, 257, 260, 266, 271.
KERTAUS
Seuraavat tehtävät ovat sopivia kokeeseen kertaamista varten
Tilastot
K30, K31, K33,
Kertymä korrelaatio
K39, K40, 6.6 toinen kirja
Todennäköisyys
K2, K5, K6
Laskusääntöjä
K21, K24, K26
Kombinatoriikka
K8, K14, K18
Jakaumat
K43, K44