Klassiseksi todennäköisyydeksi kutsutaan satunnaisilmiön todennäköisyyttä, jossa eri vaihtoehdot voidaan luetella ja ne kaikki ovat yhtä todennäköisiä.

• eri vaihtoehtoja kutsutaan alkeistapauksiksi
• hyväksyttyjä vaihtoehtoja kutsutaan suotuisiksi tapauksiksi

• alkeistapauksia 52 kpl

Esimerkki 1.

Mikä on todennäköisyys, että saadaan ässä

• ässiä 4kpl
• kortteja 52 kpl
• todennäköisyys on 4 / 52 = 1 / 13 eli noin 7,7%

Toisinaan todennäköisyys on helpompi laskea vastatapahtuman avulla

Vastatapahtuma on siis tapahtuma, jossa suotuisa alkeistapaus ei toteudu.

• mahdoton tapahtuma on tapahtuma, jonka todennäköisyys on 0
  • millä todennäköisyydellä arpakuution pisteluku on 7
• varma tapahtuma on tapahtuma, jonka todennäköisyys on 1
  • millä todennäköisyydellä satunnaisesti valittu kokonaisluku on parillinen tai pariton

Esimerkki 2.

Mäkihyppääjä pysyy pystyssä 5 kertaa peräkkäin todennäköisyydellä 35 %. Millä todennäköisyydellä hän kaatuu ainakin kerran?

• Nyt alkeistapausten avulla laskien pitäisi laskea, millä todennäköisyydellä hän kaatuu
  • 1 kerran
  • 2 kertaa
  • 3 kertaa
  • 4 kertaa
  • 5 kertaa
• tätä ei tehtävässä kerrota, joten lasketaan todennäköisyys vastatapauksen avulla
• P(kaatuu ainakin kerran) = 1 - 0,35 = 0,65 (eli 65 %)
• Tehtävän tiedoilla ei pysty laskemaan esimerkiksi sitä, millä todennäköisyydellä hän kaatuu vaikkapa 2 kertaa.

Tilastollinen todennäköisyys

Tilastollinen todennäköisyys on hyvin samankaltainen klassisen todennäköisyyden kanssa.

• Tilastollisessa todennäköisyydessä alkeistapaukset muodostuvat tilaston jo tehdyistä havainnoista.
• Usein tilastollista todennäköisyyttä käytetään ennustamiseen, mutta tämä on jonkin verran ongelmallista
  • jos en eilen jäänyt auton alle, en jää tänäänkään auton alle

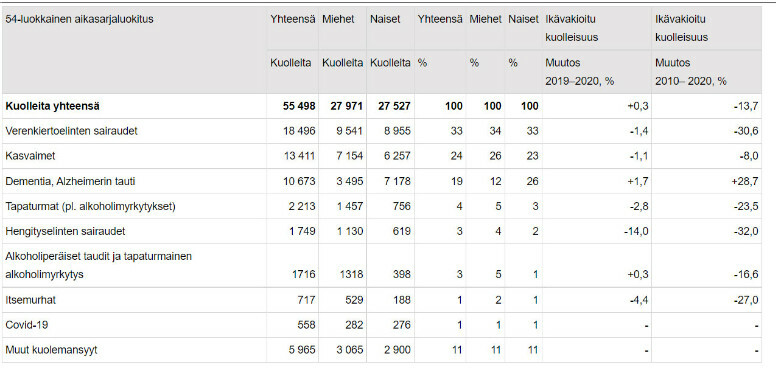
Esimerkki 3.

Millä todennäköisyydellä ihminen kuolee Koronaan (Covid-19 tautiin)

P(henkilö kuolee koronaan) = 558 / 55498 = 0,01005 (eli hyvin tarkasti 1%)

Millä todennäköisyydellä henkilö kuolee joko sydän- ja verisuonitautiin, kasvaimeen (syöpään) tai dementiaan?

P(henkilö kuolee johonkin em. tautiin) = (18496 + 13411 + 10673) / 55498 = 42580 / 55498 = 0,7672… (eli noin 77 % todennäköisyydellä)

Geometrinen todennäköisyys

Geometrisessä todennäköisyydessä lasketaan suotuisan alueen mitat ja verrataan tätä koko alueen mittoihin

• Huomaa, että geometrinen todennäköisyys voi olla yksi, kaksi tai kolmiulotteinen. Tällöin lasketaan joko pituutta, alaa tai tilavuutta.
• Geometrinen todennäköisyys vaatii usein keinotekoisen rajauksen, koska usein geometrinen mitta voi periaatteessa olla ääretön, jolloin todennäköisyys olisi aina 0.

Kotitehtäviksi: 2, 9, 11, 23, 27, 33, 38, 42, 45, 50