6. opetuskerta
Osajoukkojen lukumäärä

Mitä eroa on osajonolla ja osajoukolla
- osajonossa alkioiden järjestys vaikuttaa, eli samat alkiot eri järjestyksessä käsitetään eri jonona.
- osajoukossa merkitystä on vain sillä, mitkä alkiot osajoukosta tulevat valituiksi
Tyypillinen esimerkki osajoukkotehtävästä on lotto
lottorivit:
- 2, 7, 23, 29, 34, 35, 39 ja
- 35, 23, 7, 2, 39, 34, 29 ovat samat
Tästä seuraa siis se, että osajoukkoja on vähemmän kuin osajonoja

Merkintä luetaan ”n yli r:n”
(osajonojen tapauksessa merkintä on (n)r ja luetaan ”joukon n r permutaatio”)
Laskinohjelmassa
- osajoukkojen lukumäärä toiminnolla kombinaatioiden lukumäärä, nCr()
- osajonojen lukumäärä toiminnolla permutaatioiden lukumäärä, nPr()
Esimerkki 1, lottorivien määrä
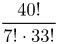
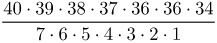
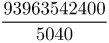

Esimerkki 6 toisella tavalla.
Esimerkki
Mikä on todennäköisyys, että lotossa ei voita mitään

Voitottomien rivien todennäköisyys yhteensä: 22,9 % + 41,6 % + 26,7 % + 7,7 % = 98,9 %
Kotitehtäviksi: 11.1, 11.3, 11.5, 11.9, 11.11, 11.13, 11.15, 11.17