7. opetuskerta
Kertolaskusääntö ja yhteenlaskusääntö
Ehdollinen ja riippumaton todennäköisyys
Jos tapahtuman todennäköisyyteen vaikuttaa joku sitä edeltävä tapahtuma todennäköisyyttä kutsutaan ehdolliseksi.
- esimerkiksi, jos korttipakasta on katsottu jo kortteja eikä pakkaa ole sekoitettu uudelleen, seuraavan kortin todennäköisyys on ehdollinen (koska jäljellä olevien korttien määrä ei ole enää 52)
- tilastolliset todennäköisyydet ovat usein ehdollisia, esimerkiksi jos tiedetään henkilön omistama automerkki, se vaikuttaa hänen kuukausitulojensa todennäköisyyteen.
Jos edeltävät tapahtumat eivät vaikuta todennäköisyyteen tapahtumat ovat riippumattomat.
- esimerkiksi jos on heitetty kolikkoa 10 kertaa ja saatu jokaisella kerralla kruuna, mikä on todennäköisyys saada seuraavalla kerralla kruuna. (0,5 mutta toisaalta edelliset tulokset voivat aiheuttaa epäilyn siitä, että kolikkoa on manipuloitu, esim. molemmat puolet ovat kruunia, jolloin todennäköisyys ei olisikaan riippumaton)
Ehdollista todennäköisyyttä merkitään

Riippumatonta todennäköisyyttä puolestaan merkitään

Laske esimerkkinä ehdollinen 50 numerosta
todennäköisyys, että saadaan 7 oikein numeroista 1-50

todennäköisyys, että saadaan pelkästään lukuja väliltä 1-40

ehdollinen todennäköisyys, että saadaan 7 oikein numeroista 1-40, kun tiedetään, että yksikään numero ei ole yli 40. Joka on siis sama kuin normaalin loton todennäköisyys.
Kaavaa, jolla ehdollinen todennäköisyys saadaan laskettua, nimitetään kertolaskusäännöksi.
Kaavalla voidaan laskea mikä tahansa kaavan todennäköisyyksistä, jos kaksi muuta pystytään selvittämään
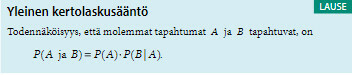
Edellinen esimerkki laskettaisiin tällä kaavalla seuraavasti:
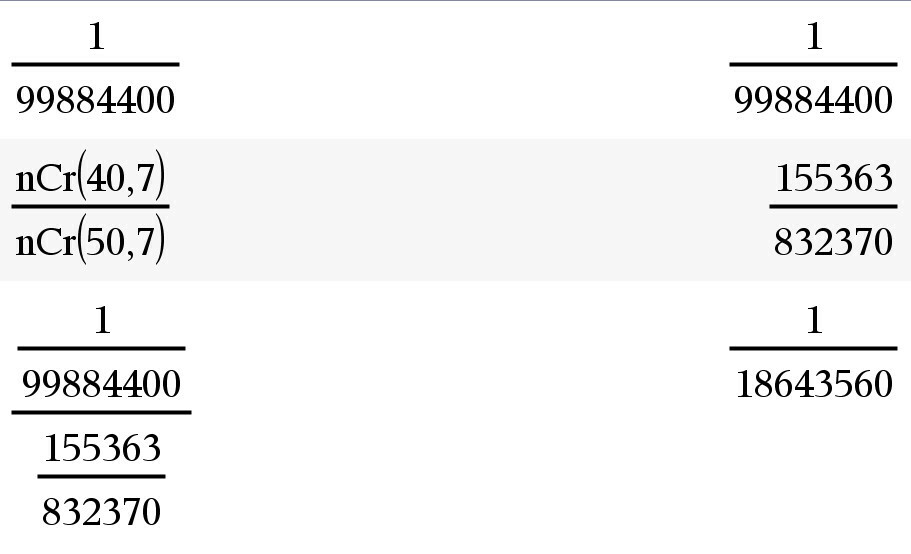
Jos tapahtumat ovat riippumattomat, kertolaskusääntö saa yksinkertaisemman muodon.

Tämä sääntö pätee esimerkiksi kaikkiin nopanheitto, kolikonheitto yms. tyyppisiin satunnaisuuksiin.
Esimerkki 2.
Todennäköisyys saada kaksi kertaa peräkkäin 6 nopalla
36 eri mahdollisuutta joten 1/36
Todennäköisyys, että saadaan kaksi kertaa peräkkäin 6, kun on saatu ensimmäisellä heitolla 6
(1/36) / (1/6) = 1/6
Yhteenlaskusääntö
Kertolaskusäännöllä lasketaan sen tyyppisiä todennäköisyyksiä, jossa A ja B molemmat tapahtuvat.
Seuraava kaava mahdollistaa laskemaan todennäköisyyksiä, jossa vähintään A tai B tapahtuu. Tämä sisältää ajatuksen, että myös silloin, jos molemmat tapahtuvat, niin ainakin toinen on tapahtunut.

Tässä kaavassa lopussa oleva - P(A ja B) johtuu siitä, että kun P(A) ja P(B) lasketaan yhteen, tulee P(A ja B) laskettua kahteen kertaan.
Silloin jos molemmat tapahtumat eivät voi tapahtua yhtä aikaa, kutsutaan tapahtumia erillisiksi tai toisensa poissulkeviksi
Tällöin yhteenlaskusääntö saa yksinkertaisemman muodon.

Tämä on hyvin helposti ymmärrettävä tilanne.
Esimerkki: laatikossa on 5 punaista pipoa, 4 sinistä pipoa, 3 keltaista pipoa ja 2 vihreää pipoa.
Millä todennäköisyydellä satunnaisesti valittu pipo on sininen tai vihreä.
Tapaukset ovat toisensa poissulkevia, joten kyseinen todennäköisyys:
P(sininen tai vihreä) = 4 / 14 + 2 / 14 = 6 / 14 » 0,429
Kotitehtäviksi: 12.1, 12.4, 12.6, 12.14, 12.17, 13.1, 13.3, 13.5, 13.19, 13.21