Teoria T2 suorankulmaisen kolmion sivun pituuden laskeminen trigonometristen funktioden avulla
Pythagoraan lauseen avulla pystyimme selvittämään suorakulmaisen kolmion tuntemattoman sivun pituuden, kun tunnettiin kaksi suorakulmaisen kolmion sivua.
Trigonometristen funktioiden avulla suorakulmaisen kolmion sivun pituus voidaan selvittää, kun tunnetaan yhden sivun pituus ja toisen terävän kulman suuruus.
Ohje:
1. Piirrä tehtävän tilanteesta kuva ellei sitä ole valmiina.
2. Merkitse tuntematonta sivun pituutta muuttujalla (usein x:llä).
3. Tunnista mikä on terävän kulman suuruus.
4. Tunnista mitkä sivun pituudet on merkitty kuvaan (terävän kulman viereinen/vastainen kateetti tai hypotenuusa).
5. Tunnista mitä funktiota pitää tehtävässä käyttää (sini, kosini, tangentti).
6. Muodosta funktion mukainen yhtälö ja ratkaise sivun pituus eli tuntematon x aikaisemmilta kursseilta tutulla tavalla..
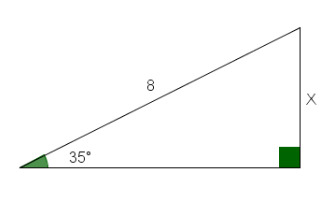
Esimerkki 1. Ratkaise sivun x pituus.
Ratkaisu:
1. Kuva on jo valmiina.
2. Tuntematon sivu on merkittu jo valmiiksi.
3. Funktio pitää määrittää aina terävästä kulmasta katsottuna, nyt kulmasta 35°.
4. Kuvasta nähdään, että kulman 35° vastainen kateetti on tuntematon x ja pisin sivu eli hypotenuusa on 8.
5. Trigonometrinen funtio, jossa mainitaan kulman vastainen kateetti ja hypotenuusa on sini.
6. Muodostetaan sinifunktio kulmasta 35°, jolloin voidaan kirjoittaa
sin 35° [[$ = \frac{x}{8}. $]]
Ratkaistaan yhtälöstä x kuten olemme jo aikaisemmilta kursseilta oppineet eli aloitetaan kertomalla molemmat puolet luvulla 8.
sin 35° [[$ = \frac{x}{8} \quad $]] || [[$ \cdot 8 $]]
[[$ 8 \cdot $]]sin 35° [[$ = x $]]
[[$ 4,588611... = x $]]
[[$ x \approx 4,6 $]]
Esimerkki 2. Suorakulmaisen kolmion 20° kulman viereinen kateetti on 5cm. Ratkaise kolmiosta hypotenuusan pituus.
Ratkaisu:
1. Piirretään mallikuva.
2. Merkataan tuntematonta hypotenuusaa kirjaimella x.
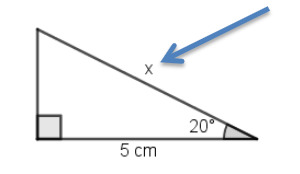
3. Funktio pitää määrittää aina terävästä kulmasta katsottuna, nyt kulmasta 20°.
4. Kuvasta nähdään, että kulman 20° viereinen kateetti on tuntematon 5 cm ja pisin sivu eli hypotenuusa on x.
5. Trigonometrinen funtio, jossa mainitaan kulman viereinen kateetti ja hypotenuusa on kosini.
6. Muodostetaan kosinifunktio kulmasta 20°, jolloin voidaan kirjoittaa
cos 20° [[$ = \frac{5}{x}. $]]
Ratkaistaan yhtälöstä x kuten olemme jo aikaisemmilta kursseilta oppineet eli aloitetaan kertomalla molemmat puolet luvulla x.
cos 20° [[$ = \frac{5}{x} \quad $]] || [[$ \cdot x $]]
[[$ x \cdot $]]cos 20° [[$ = 5 $]] || : cos 20°
[[$ x = \frac{5}{cos 20°} $]]
[[$ x \approx 5,3 $]]
Vastaus: Hypotenuusan pituus on 5,3 cm.
Trigonometristen funktioiden avulla suorakulmaisen kolmion sivun pituus voidaan selvittää, kun tunnetaan yhden sivun pituus ja toisen terävän kulman suuruus.
Ohje:
1. Piirrä tehtävän tilanteesta kuva ellei sitä ole valmiina.
2. Merkitse tuntematonta sivun pituutta muuttujalla (usein x:llä).
3. Tunnista mikä on terävän kulman suuruus.
4. Tunnista mitkä sivun pituudet on merkitty kuvaan (terävän kulman viereinen/vastainen kateetti tai hypotenuusa).
5. Tunnista mitä funktiota pitää tehtävässä käyttää (sini, kosini, tangentti).
6. Muodosta funktion mukainen yhtälö ja ratkaise sivun pituus eli tuntematon x aikaisemmilta kursseilta tutulla tavalla..
Esimerkki 1. Ratkaise sivun x pituus.

Ratkaisu:
1. Kuva on jo valmiina.
2. Tuntematon sivu on merkittu jo valmiiksi.
3. Funktio pitää määrittää aina terävästä kulmasta katsottuna, nyt kulmasta 35°.
4. Kuvasta nähdään, että kulman 35° vastainen kateetti on tuntematon x ja pisin sivu eli hypotenuusa on 8.
5. Trigonometrinen funtio, jossa mainitaan kulman vastainen kateetti ja hypotenuusa on sini.
6. Muodostetaan sinifunktio kulmasta 35°, jolloin voidaan kirjoittaa
sin 35° [[$ = \frac{x}{8}. $]]
Ratkaistaan yhtälöstä x kuten olemme jo aikaisemmilta kursseilta oppineet eli aloitetaan kertomalla molemmat puolet luvulla 8.
sin 35° [[$ = \frac{x}{8} \quad $]] || [[$ \cdot 8 $]]
[[$ 8 \cdot $]]sin 35° [[$ = x $]]
[[$ 4,588611... = x $]]
[[$ x \approx 4,6 $]]
Esimerkki 2. Suorakulmaisen kolmion 20° kulman viereinen kateetti on 5cm. Ratkaise kolmiosta hypotenuusan pituus.
Ratkaisu:
1. Piirretään mallikuva.
2. Merkataan tuntematonta hypotenuusaa kirjaimella x.

3. Funktio pitää määrittää aina terävästä kulmasta katsottuna, nyt kulmasta 20°.
4. Kuvasta nähdään, että kulman 20° viereinen kateetti on tuntematon 5 cm ja pisin sivu eli hypotenuusa on x.
5. Trigonometrinen funtio, jossa mainitaan kulman viereinen kateetti ja hypotenuusa on kosini.
6. Muodostetaan kosinifunktio kulmasta 20°, jolloin voidaan kirjoittaa
cos 20° [[$ = \frac{5}{x}. $]]
Ratkaistaan yhtälöstä x kuten olemme jo aikaisemmilta kursseilta oppineet eli aloitetaan kertomalla molemmat puolet luvulla x.
cos 20° [[$ = \frac{5}{x} \quad $]] || [[$ \cdot x $]]
[[$ x \cdot $]]cos 20° [[$ = 5 $]] || : cos 20°
[[$ x = \frac{5}{cos 20°} $]]
[[$ x \approx 5,3 $]]
Vastaus: Hypotenuusan pituus on 5,3 cm.