3. Määrätty integraali
Määrätty integraali
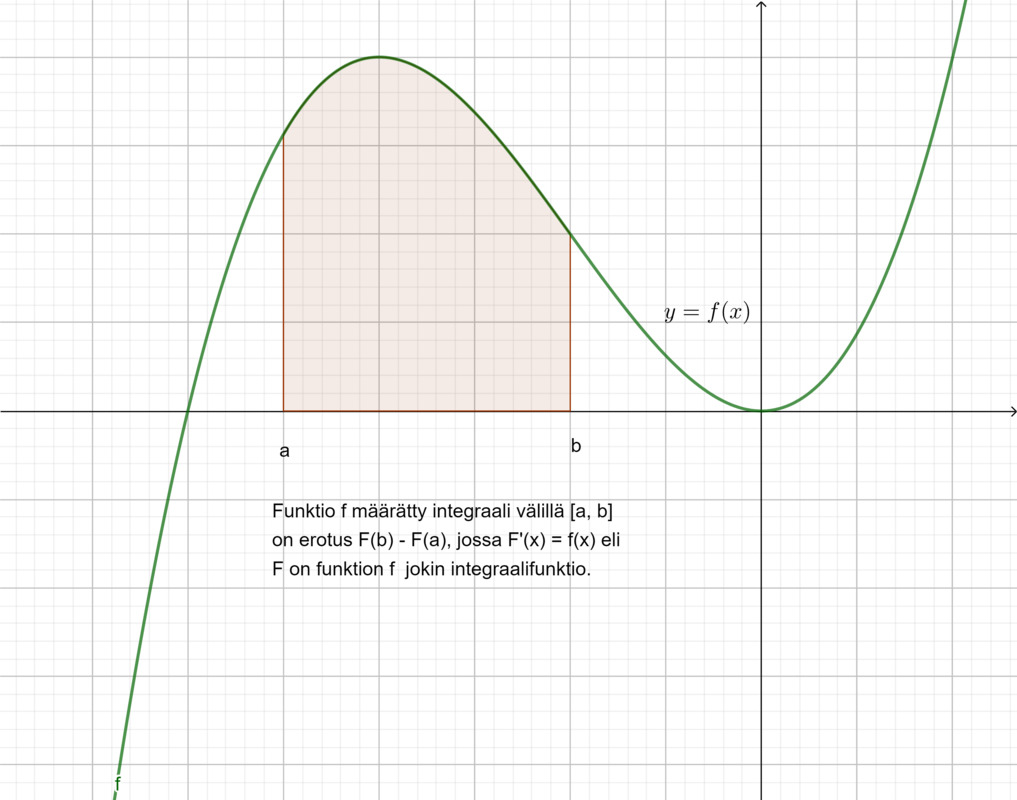
Määrätyn integraalin merkitseminen
Funktion f määrätty integraali välillä [a, b] on erotus F(b) - F(a), jossa F'(x) = f(x).
Tätä määrättyä integraalia merkitään
Esim
Määritä
a)
b)
Määritä
Määrätyn integraalin ominaisuuksia
1. Integroimisvälin jakaminen osiin
2.
Jos on samat integroimisrajat niin summan integrointia käytetään usein oikelta vasemmalle
3. Tyhjä integroimisväli eli ylä- ja alaraja ovat samat
4. Integroimismuuttujan vaihto
5. Integroimisrajojen vaihtaminen