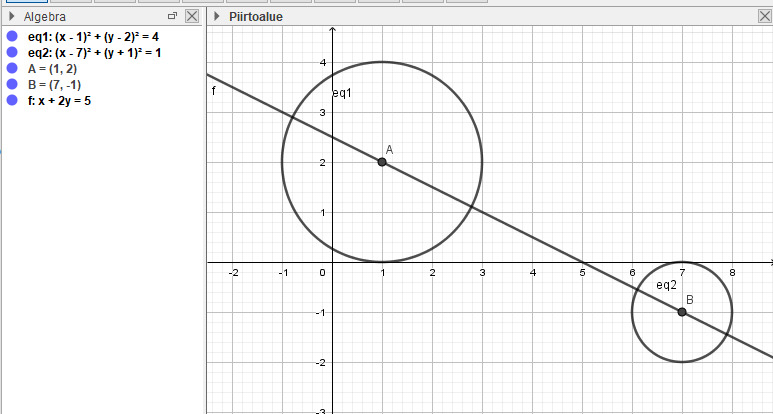
4.2 Ympyrän yhtälö yhteisessä muodossa
431
muutetaan ympyröiden yhtälöt keskipistemuotoisiksi, jotta nähdään niiden keskipiste ja säde

%5E2%2B%5Cleft(y-3%5Cright)%5E2%3D18)
%7B%2C%7D%5C%20r%3D3%5Csqrt%7B2%7D)

%5E2%2B%5Cleft(y-3%5Cright)%5E2%3D23)
%7B%2C%7D%5C%20r%3D%5Csqrt%7B23%7D)
ympyrät sijaitsevat sisäkkäin, niiden keskipisteiden etäisyyksien erotus on pienempi kuin säteiden erotus
ympyrät sijaitsevat sisäkkäin, niiden keskipisteiden etäisyyksien erotus on pienempi kuin säteiden erotus
430
muutetaan ympyröiden yhtälöt keskipistemuotoisiksi, jotta voidaan laskea keskipisteiden välisen etäisyyden ja säteiden erotus

%5E2%2B%5Cleft(y-3%5Cright)%5E2%3D5)
%7B%2C%7D%5C%20r%3D%5Csqrt%7B5%7D)

%5E2%2B%5Cleft(y-2%5Cright)%5E2%3D20)
%7B%2C%7D%5C%20r%3D2%5Csqrt%7B5%7D)
%5E2%2B%5Cleft(y_1-y_2%5Cright)%5E2%7D)


)
pisteiden välinen etäisyys
ympyröiden välinen etäisyys on pisteiden välisen etäisyyden ja ympyröiden säteiden erotus