suora leikkaa xy-tason pisteessä (-6,9,0)
suora leikkaa z-akselin pisteessä (0,0,6)

421

$x^2=\left(-4\right)^2+3^2$
$x=5$

$x^2=12^2+5^2$
$x=13$

422

$1\ asteikon\ ruutu\ kuvaa\ 1km^2$
$100km-50km=50km$
$\frac{50}{5}=10$
$meteoriitti\ kulkee\ 10\ koordinaatiston\ väliä$
$10\left(\overline{\text{i}}+3\overline{\text{j}}\right)=10\overline{\text{i}}+30\overline{\text{j}}$
$\left|10\overline{\text{i}}+30\overline{\text{j}}\right|=10\sqrt{10}\approx31{,}622...km$

420

a) kohtisuorassa xy-tasoa vastaan
$\begin{cases} x=1&\\ y=2&\\ z=3t& \end{cases}$

b) yhdensuuntainen y-akselin kanssa

$\begin{cases} x=1&\\ y=2t&\\ z=3& \end{cases}$

c) yhdensuuntainen pisteiden (1,0,1) ja (2,1,3) kautta kulkevan suoran kanssa

$\begin{cases} x=1+t&\\ y=2+t&\\ z=3+2t& \end{cases}$

419

kaikki yhtälöt A-D esittävät suoraa a, koska ne alkavat samasta pisteestä ja niiden muodostamien suorien suuntavektorit ovat yhdensuuntaiset

414

a)
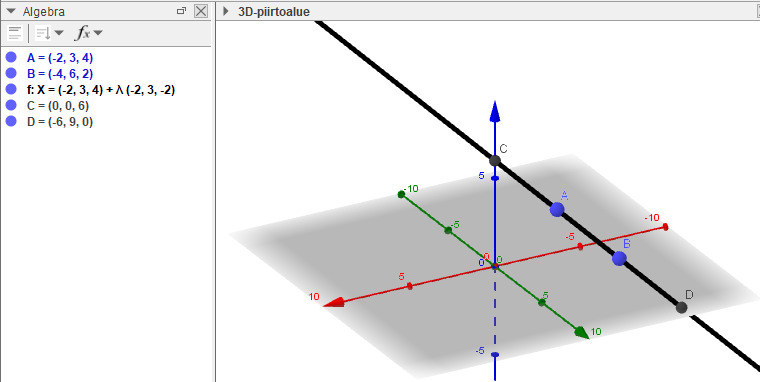
suorat voivat myös olla yhdensuuntaiset tai ristikkäiset, jolloin ne eivät leikkaa
esimerkiksi nämä avaruuden suorat ovat yhdensuuntaiset, eivätkä leikkaa
$\begin{cases} x=0&\\ y=0&\\ z=t& \end{cases}$
$\begin{cases} x=1&\\ y=0&\\ z=t& \end{cases}$
b)
suora voi myös kulkea xy-tason suuntaisesti koskematta tasoon, esimerkiksi

$\begin{cases} x=1&\\ y=t&\\ z=1& \end{cases}$
c)
suoran ei ole pakko leikata mitään akselia, vaan se voi olla niiden kanssa ristikkäinen, esimerkiksi

$\begin{cases} x=2t+1&\\ y=t&\\ z=t+1& \end{cases}$

411

b)
$\overline{s}=3\overline{\text{i}}-2\overline{\text{j}}$

$\begin{cases} x=-5+3t&\\ y=4-2t&t\in\mathbb{R} \end{cases}$

$b=2\overline{\text{i}}+\overline{\text{j}}$
$\begin{cases} x=6+2r&\\ y=3+r&r\in\mathbb{R} \end{cases}$
$\begin{cases} -5+3t=6+2r&\\ 4-2t=3+r&\parallel\cdot\left(-2\right) \end{cases}$
$\begin{cases} -5+3t=6+2r&\\ -8+4t=-6-2r& \end{cases}$
$7t=13{,}\ t=\frac{13}{7}$
$ratkaistaan\ r\ sijoittamalla\ t\ yhtälöpariin$
$\begin{cases} -5+3\cdot\frac{13}{7}=6+2r&\\ 4-2\cdot\frac{13}{7}=3+r& \end{cases}$
$\begin{cases} -\frac{38}{7}=2r&\\ -\frac{19}{7}=r& \end{cases}$
$3r=-\frac{57}{7}{,}\ r=-\frac{19}{7}$
$sijoitetaan\ t\ suoran\ a\ yhtälöön$
$\begin{cases} x=-5+\frac{39}{7}&\\ y=4-\frac{26}{7}& \end{cases}$
$\begin{cases} x=\frac{4}{7}&\\ y=\frac{2}{7}& \end{cases}$
$suorat\ a\ ja\ b\ leikkaavat\ pisteessä\ \left(\frac{4}{7}{,}\ \frac{2}{7}\right)$

410

a)
$A=\left(-53{,}\ 18{,}\ 71\right)$
$OA=OP+t\overline{v}$
$P=\left(10{,}-27{,}7\right)$
$\overline{v}=7\overline{\text{i}}-5\overline{\text{j}}-8\overline{\text{k}}$
$-53\overline{\text{i}}+18\overline{\text{j}}+71\overline{\text{k}}=10\overline{\text{i}}-27\overline{\text{j}}+7\overline{\text{k}}+7t\overline{\text{i}}-5t\overline{\text{j}}-8t\overline{\text{k}}$

$\begin{cases} -53=7t+10&t=-9\\ 18=-5t-27&t=-9\\ 71=-8t+7&t=-8 \end{cases}$

piste A ei ole suoralla

b)

$B=\left(2{,}\ -4{,}\ 5\right)$
$C=\left(-8{,}\ 0{,}\ 17\right)$
$suoran\ suuntavektori=\overline{BC}$
$\overline{BC}=-10\overline{\text{i}}-4\overline{\text{j}}+12\overline{\text{k}}$
$\overline{OA}=\overline{OB}+t\overline{v}$
$-53\overline{\text{i}}+18\overline{\text{j}}+71\overline{\text{k}}=2\overline{\text{i}}-4\overline{\text{j}}+5\overline{\text{k}}-10t\overline{\text{i}}-4t\overline{\text{j}}+12t\overline{\text{k}}$

$\begin{cases} -53=2-10t&t=5{,}5\\ 18=-4-4t&t=5{,}5\\ 71=5+12t&t=5{,}5 \end{cases}$

Piste A on suoralla

409

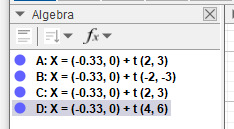
Mitkä vaihtoehdoista A-D esittävät suoraa $\begin{cases} x=-1+3t&\\ y=2-t&t\in\mathbb{R} \end{cases}$
ABC

408

a)
$\overline{OP}=\overline{OA}+t\overline{v}$
$\overline{OP}=2i-k+t\left(-\overline{\text{i}}+3\overline{\text{j}}-4\overline{\text{k}}\right)$
$suuntavektori\ on\ -\overline{\text{i}}+3\overline{\text{j}}-4\overline{\text{k}}$
$jokin\ suoran\ piste\ on\ \left(2{,}0{,}-1\right)$
b)
$\begin{cases} x=2-t&\\ y=3&\\ z=5t&t\in\mathbb{R} \end{cases}$
$suuntavektori\ on\ \left(2-t\right)\overline{\text{i}}+3\overline{\text{j}}+5t\overline{\text{k}}$
$jokin\ suoran\ piste$
$suoran\ piste\ kun\ t=0$
$\left(2{,}\ 3{,}\ 0\right)$

417

$\begin{cases} x=3-2t&\\ y=-1+2t&\\ z=3-t&t\in\mathbb{R} \end{cases}$
$suora\ kulkee\ pisteen\ B\left(3{,}\ -1{,}\ 3\right)\ kautta$

$ja\ suoran\ suuntavektori\ on\ -2\overline{\text{i}}+2\overline{\text{j}}-\overline{\text{k}}$

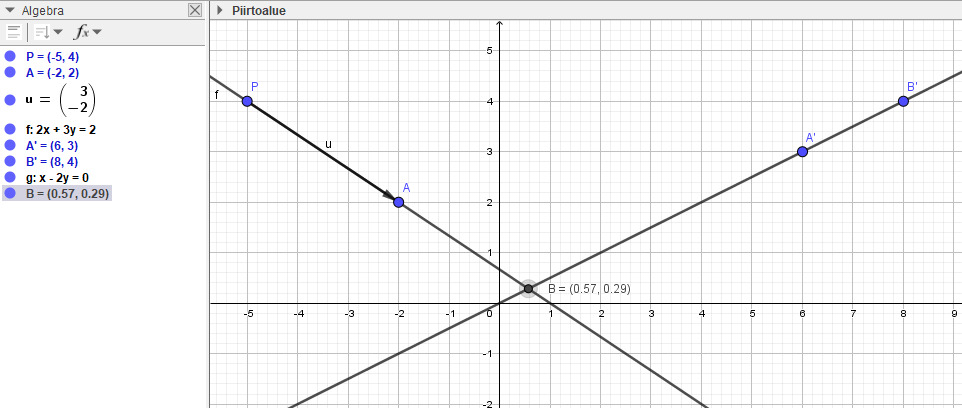
Pisteen A etäisyys suorasta on kohtisuorasti mitattu etäisyys

toisaalta etäisyys on vektorin $\overline{AA'}$ pituus

Piste A' on suoralla, joten sen koordinaatit ovat muotoa $\left(3-2t{,}\ -1+2t{,}\ 3-t\right){,}\ t\in\mathbb{R}$

$\overline{AA'}=-2t\overline{\text{i}}-12+2t\overline{\text{j}}-6-t\overline{\text{k}}$

Nyt

$\overline{AA'}\perp\overline{s}$

joten

$\overline{AA'}\cdot\overline{s}=0$
$\overline{AA'}\cdot\overline{s}=-2t\cdot-2+\left(-12+2t\right)\cdot2+\left(-6-t\right)\cdot\left(-1\right)=0$
$9t-18=0$
$t=2$
$\overline{AA'}=-4\overline{\text{i}}-8\overline{\text{j}}-8\overline{\text{k}}$
$\left|\overline{AA'}\right|=\sqrt{4^2+8^2+8^2}=12\ \left(tai\ -12\right)$
$pisteen\ A\ \left(3{,}\ 11{,}\ 3\right)\ etäisyys\ suorasta\ on\ 12\$

Oskari Lahtinen

4.1 Suora tasossa ja avaruudessa

412

413

421

422

420

419

414

411

410

409

408

417