Esimerkit
Kpl.4.3
446
%3D%5Ccos2x%2B2%5Csin%20x)
%3D-2%5Csin2x%2B2%5Ccos%20x)
%3D0)


%3D0)









%3D%5Ccos%5Cleft(2%5Ccdot0%5Cright)%2B2%5Csin0%3D1%2B2%5Ccdot0%3D1)
%3D%5Ccos%5Cleft(2%5Ccdot2%5Cpi%5Cright)%2B2%5Csin%5Cleft(2%5Cpi%5Cright)%3D1%2B2%5Ccdot0%3D1)
%3D1)
%3D-3)
%3D%5Cfrac%7B3%7D%7B2%7D)
%3D%5Cfrac%7B3%7D%7B2%7D)
Sinifunktion sinx perujakso on 2π ja cos2x perusjakso on 2π/2=π. Funktion cos2 arvot toistuvat samoina π:n välein
ja myös 2π:n välein. Siis funktioniden sinix ja cos2x arvot toistuvat samoina 2π:n välein eli funktion f(x) jakso on 2π.
Riittää etsiä funktion f(x) suurin ja pienin arvo välillä [0,2π].
Suljetulla välillä jatkuva funktio saa suurimman ja pienimmän arvonsa välin pätepisteisä tai välillä olevissa derivaatan nollakohdissa.
tai
Välillä [0,2π] ovat nollatkohdat
Lasketaan funktion arvot välin päätepisteissä ja välillä olevissa derivaatan nollakohdissa
Arvojoukko om [-3,3/2]
Kpl.4.2
Esim. Derivoi
a)
b)
c)
Kpl.4.1
Määritelmä
) on ulkofunktio ja
on ulkofunktio ja ) on sisäfunktio
on sisäfunktio
%5Cleft(x%5Cright)%3Du%5Cleft(s%5Cleft(x%5Cright)%5Cright)%3Du%5Cleft(3x%2B1%5Cright)%5E2)
%5Cleft(x%5Cright)%3Ds%5Cleft(u%5Cleft(x%5Cright)%5Cright)%3Ds%5Cleft(x%5Cright)%5E2%3D3x%5E2%2B1)
%3D%5Ccos%20x) ja
ja%3Dx%5E2%2B1)
%3Du%5Cleft(s%5Cleft(x%5Cright)%5Cright)%3Du%5Cleft(x%5E2%2B1%5Cright)%3D%5Ccos%5Cleft(x%5E2%2B1%5Cright))
%3Ds%5Cleft(u%5Cleft(x%5Cright)%5Cright)%3Ds%5Cleft(%5Ccos%20x%5Cright)%3D%5Cleft(%5Ccos%20x%5Cright)%5E2%2B1%3D%5Ccos2x%2B1%5Cright))
%5Cleft(x%5Cright)%5Cne%5Cleft(s%5Ccirc%20u%5Cright)%5Cleft(x%5Cright))
%3D%5Cleft(3x%5E2%2B2x%5Cright)%5E2)
%3D3x%5E2%2B2x) ,
,%3Dx%5E2)
%5Cright)%3Du%5Cleft(3x%5E2%2B2x%5Cright)%3D%5Cleft(3x%5E2%2B2x%5Cright)%5E2)
%3D%5Cfrac%7B3%7D%7B1%2B%5Csin%20x%7D)
%3D1%2B%5Csin%20x) ,
,%3D%5Cfrac%7B3%7D%7Bx%7D)
%5Cright)%3Du%5Cleft(%5Cfrac%7B3%7D%7B1%2B%5Csin%20x%7D%5Cright))
%3D%5Csin%20x) ,
,%3D%5Cfrac%7B3%7D%7B1%2Bx%7D)
%5Cright)%3Du%5Cleft(%5Cfrac%7B3%7D%7B1%2B%5Csin%20x%7D%5Cright))
Lauseke%5Cright)) on funktioiden
on funktioiden ) ja
ja) yhdistetty funktio
yhdistetty funktio
Määtitään%5Cleft(x%5Cright)%3Du%5Cleft(s%5Cleft(x%5Cright)%5Cright))
Esim. Muodosta
a)%5E2) ja
ja%5E2%3D3x%2B1)
b)
Huom! yleensä
Esim.Tulkitse yhdistetyksi funktioksi
a)
Tällöin
b)
Tapa 1:
Tapa 2:
Kpl.3.2
Lause

Lause



 , niin
, niin  ja
ja eli yhtälö on epätosi.
eli yhtälö on epätosi.
 Todistus
Todistus
%7D%7Bg%5Cleft(x%5Cright)%7D%3D%5Cfrac%7Bf%27%5Cleft(x%5Cright)g%5Cleft(x%5Cright)-f%5Cleft(x%5Cright)g%27%5Cleft(x%5Cright)%7D%7B%5Cleft(g%5Cleft(x%5Cright)%5Cright)%5E%7B%5E2%7D%7D)


%5E2%7D%3D%5Cfrac%7B%5Ccos%5E2x%2B%5Csin%5E2x%7D%7B%5Ccos%5E2x%7D%3D%5Cfrac%7B1%7D%7B%5Ccos%5E2x%7D)
%5E2%7D%7B%5Cleft(%5Ccos%20x%5Cright)%5E%7B%5E2%7D%7D%3D1%2B%5Cleft(%5Ctan%20x%5Cright)%5E2%3D1%2B%5Ctan%5E2x)
Tangenttifunktiolle %3D%5Ctan%20x) pätee:
pätee:
- Funktio on määritelty, kun 
- Arvojoukko on ]-∞,∞[ eli ℝ
- Jatkuva määrittelyjoukossaan
- Funktio on jaksollinen, perusjakso on π
- Funktio on kasvava kaikilla määtittelyjoukkonsa osaväleillä
Esim. Ratkaise yhtälö geogebralla arvioiden ja ilman apuvälineitä
a) ![\tan x=2+\sqrt[]{3}](https://math-demo.abitti.fi/math.svg?latex=%5Ctan%20x%3D2%2B%5Csqrt%5B%5D%7B3%7D)
Geogebra: 
MAOL: Eräs ratkaisu on  . Kaikki ratkaisut ovat
. Kaikki ratkaisut ovat
b)
Geogebralla: 



Lause
Jos on yhtälön
on yhtälön  eräs ratkaisu, niin kaikki ratkaisut ovat
eräs ratkaisu, niin kaikki ratkaisut ovat 
Esim. Ratkaise yhtälö
Jos
Lause
tai
Kpl.3.1
Kpl.2.2
2.2 sinin ja kosinin derivaatat
Lause
Esim. Määritä
a) f'(x), kun f(x)=2sinx+cosx
b) f'(π/2), kun f(x)=sinx-3cosx
Esim. Derivoi
a) h(x)=x³cosx
b) %3D%5Cfrac%7B%5Csin%20x%7D%7B%5Ccos%20x%7D)
Kpl.2.1
Molemmille funktiolle Esim. Määritä funktion arvojoukko, kun
- Funktio on määritelty x∈ℝ
- Funktion arvojoukko on [-1,1]
- Funktio on jatkuva
- Funktion kuvaaja toistuu samanlaisena 2π:n välein
Esim Määritä funktion joukko, kun
%3D3%5Csin%20x-2)



eli arvojoukko on [-5,1]
Lause
Funktioiden
214
Arvo kohdassa x=0
sinin arvot ovat välillä [-1,1], joten yhtälöllä ei ole ratkaisua, eikä funktiolla ole nollakohtia.
Arvojoukko on [2,8]
Kpl.1.4
Esim. Ratkaise kaikki kulmat x, jolle ![\sin x=\frac{1}{\sqrt[]{2}}](https://math-demo.abitti.fi/math.svg?latex=%5Csin%20x%3D%5Cfrac%7B1%7D%7B%5Csqrt%5B%5D%7B2%7D%7D)
MAOL: Kulmat  on yhtälön eräs ratkaisu
on yhtälön eräs ratkaisu
koska ) , niin myös
, niin myös  on yhtälön ratkaisu
on yhtälön ratkaisu
kaikki ratkaisut ovat
Lause: Jos yhtälöllä on yksi ratkaisu x=α, niin kaikki ratkaisut ovat
on yksi ratkaisu x=α, niin kaikki ratkaisut ovat  tai
tai 
Esim. Ratkaise yhtälö ![\sqrt[]{2}\cos x+1=0](https://math-demo.abitti.fi/math.svg?latex=%5Csqrt%5B%5D%7B2%7D%5Ccos%20x%2B1%3D0)
MAOL: yksi ratkaisu on 
koska
Kaikki ratkaisut ovat  tai
tai
Lause: Jos yhtälöllä
t.173
MAOL: Kulman sini on
sini on ![-\frac{1}{\sqrt[]{2}}](https://math-demo.abitti.fi/math.svg?latex=-%5Cfrac%7B1%7D%7B%5Csqrt%5B%5D%7B2%7D%7D)
Selvitetään, mitkä ratkaisut ovat välillä ]-12π,12π[ eli ]-48π,48π[
Ratkaisutista halutulle välille kuuluvat
Esim. Ratkaise
Kpl.1.3
Esim. Laske ilmna laskinta
a)
c) Osoita, että 
Lause: Kaksinkertaisen kulman sini ja kosini
Esim. Tidetään, että . Määritä cos2α ja sin2α
. Määritä cos2α ja sin2α
tai
Kpl.1.2
Määritä taulukkokirjan avulla

)

![\cos\left(-\frac{\pi}{6}\right)=\cos\left(-\frac{\pi}{6}+2\pi\right)=\cos\frac{11\pi}{6}=\frac{\sqrt[]{3}}{2}](https://math-demo.abitti.fi/math.svg?latex=%5Ccos%5Cleft(-%5Cfrac%7B%5Cpi%7D%7B6%7D%5Cright)%3D%5Ccos%5Cleft(-%5Cfrac%7B%5Cpi%7D%7B6%7D%2B2%5Cpi%5Cright)%3D%5Ccos%5Cfrac%7B11%5Cpi%7D%7B6%7D%3D%5Cfrac%7B%5Csqrt%5B%5D%7B3%7D%7D%7B2%7D)
![\cos\frac{17\pi}{6}=\cos\frac{17}{6}\pi=\cos2\frac{5}{6}\pi=\cos\left(2\pi+\frac{5}{6}\pi\right)=\cos\frac{5\pi}{6}=-\frac{\sqrt[]{3}}{2}](https://math-demo.abitti.fi/math.svg?latex=%5Ccos%5Cfrac%7B17%5Cpi%7D%7B6%7D%3D%5Ccos%5Cfrac%7B17%7D%7B6%7D%5Cpi%3D%5Ccos2%5Cfrac%7B5%7D%7B6%7D%5Cpi%3D%5Ccos%5Cleft(2%5Cpi%2B%5Cfrac%7B5%7D%7B6%7D%5Cpi%5Cright)%3D%5Ccos%5Cfrac%7B5%5Cpi%7D%7B6%7D%3D-%5Cfrac%7B%5Csqrt%5B%5D%7B3%7D%7D%7B2%7D)
a)
b)
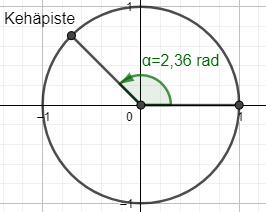
Etsitään välin [0,2π] kulma, jolla on sama kehäpiste kuin kulmalla . Lisätään kulmaan
. Lisätään kulmaan täysiä kulmia, kunnes saadaan postiivinen kulma.
täysiä kulmia, kunnes saadaan postiivinen kulma.
c)
Kpl.1.1
Määritelmä:
Kulman suurus radiaaneina on kulmaa vastaavan ympyrän kaaren pituus kun ympyrän säde on 1 ja ympyrän keskipiste on kulma kärki.










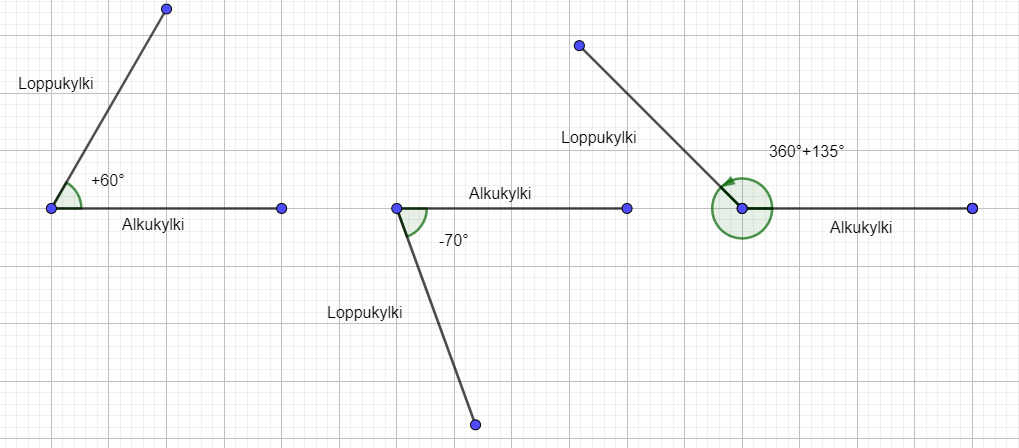
- Suunnatulla kulmalla on alku- ja loppukylki


b)
)
Kulman suurus radiaaneina on kulmaa vastaavan ympyrän kaaren pituus kun ympyrän säde on 1 ja ympyrän keskipiste on kulma kärki.
Esim. Munna
a)
 asteiksi
asteiksi
b)
 asteiksi
asteiksi
c)
) asteiksi
asteiksi
d)
 radiaaneiksi
radiaaneiksi
- Suunnatulla kulmalla on alku- ja loppukylki
- Positiivisen kulman kiertosuunta on vastapäivään
- Negatiivisen kulma kiertosuunta on myötäpäivään
- Kulman kärki on origossa
- Alkukylki on posit. x-akseli
- Loppukyljen- ja ympyrän lp. on kehäpiste

Esim. Piirrä yksikköympyrälle sueraavat kulmat ja merkitse vastaavat kehäpisteet
a)

b)