MA3P
S.178 T.470
S.178 T.466
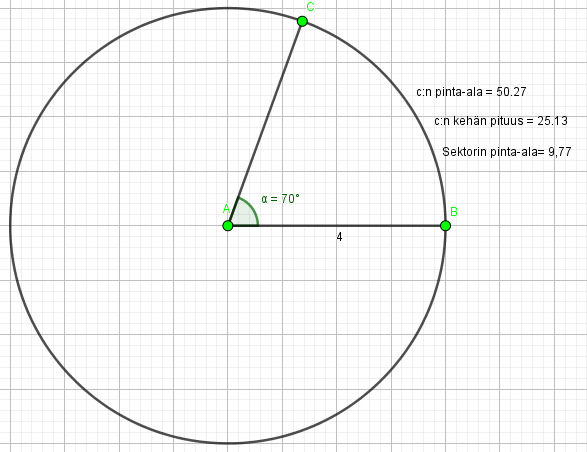
a)%5E3%7D%7B2%7D%3D2094%7B%2C%7D395...%5Capprox2100%5Cleft(cm%5E3%5Cright))
b)
%5E2%7D%7B2%7D%3D200%5Cpi%3D628%7B%2C%7D318...%5Capprox628%5Cleft(cm%5E2%5Cright))
c)
)
b)
c)
S.177 T.465
S.177 T.464
S.168 T.447
a)
![h=\sqrt[]{7{,}8^2-\left(\frac{6}{2}\right)^2}](https://math-demo.abitti.fi/math.svg?latex=h%3D%5Csqrt%5B%5D%7B7%7B%2C%7D8%5E2-%5Cleft(%5Cfrac%7B6%7D%7B2%7D%5Cright)%5E2%7D)

%5E2%5Ccdot7%7B%2C%7D2%3D67%7B%2C%7D858...%5Capprox68%5C%20%5Cleft(cm%5E2%5Cright))
%5E2%5Cpi%3D9%5Cpi28%7B%2C%7D274...%5Capprox28%5Cleft(cm%5E2%5Cright))
)
b)
![x=\sqrt[]{2{,}9^2-2^2}](https://math-demo.abitti.fi/math.svg?latex=x%3D%5Csqrt%5B%5D%7B2%7B%2C%7D9%5E2-2%5E2%7D)

![h=\sqrt[]{2{,}1^2-2^2}](https://math-demo.abitti.fi/math.svg?latex=h%3D%5Csqrt%5B%5D%7B2%7B%2C%7D1%5E2-2%5E2%7D)
)
)
)
)
b)
S.168 T.444
S.158 T.427
S.157 T.425
S.149 T.408
S.148 T.405
S.136 T.354
S.134 T.346
S.124 T.334
S.122 T.333
S.122 T.330
S. 122 T. 327
S.114 T.314
S.114 T.313
S.112 T.302
S.102 T.275
S.102 T.267
S.93 T.258
S.93 T.253
S.93 T.252
S.83 T.225
a)






b)
c)
S.83 T.223
a)
b)
S.72 T.207
a)
b)
S.72 T.205
S.56 T.174
a) Tosi, koska neliöllä on aina samanpituiset sivut ja samankokoiset kulmat.
b) Epätosi, koska eri suorakulmioiden leveys ja korkeus voi olla erilaisessa mittakaavassa.
c) Epätosi, yhdenmuotoisuuteen tarvitaan kaksi samankokoista kulmaa.
d) Tosi, jos korkeus on sama, niiden pinta-alatkin ovat oltava samat.
b) Epätosi, koska eri suorakulmioiden leveys ja korkeus voi olla erilaisessa mittakaavassa.
c) Epätosi, yhdenmuotoisuuteen tarvitaan kaksi samankokoista kulmaa.
d) Tosi, jos korkeus on sama, niiden pinta-alatkin ovat oltava samat.
S.56 T.172
a) Ovat, koska iillä on aina samanpituiset sivut ja samankokoiset kulmat, jolloin ne ovat aina yhtenevät.
b) AB:n välissä, koska silloin EF jakaa sunnikan kahden eri sunnikaan, ja lävistäjän avulla sunnikas taas puolintuu, loppuksi jäljellä jäävät kolmiot ovat yhtenevät.
b) AB:n välissä, koska silloin EF jakaa sunnikan kahden eri sunnikaan, ja lävistäjän avulla sunnikas taas puolintuu, loppuksi jäljellä jäävät kolmiot ovat yhtenevät.
S.56 T.176
S.56 T.175
S.56 T.171
a)


%5E2)




b)
S.42 T.152
S.42 T.148
S.29 T.133
S.28 T.124
a)
)
b)




![x^2=64\ \ \ \ \ \left|\right|\sqrt[]{}](https://math-demo.abitti.fi/math.svg?latex=x%5E2%3D64%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft%7C%5Cright%7C%5Csqrt%5B%5D%7B%7D)
)
)
c)
)
d)
)
)

b)
c)
d)
S.19 T.110
S.18 T.106
a)
Suorat a ja b ovat yhdensuuntaiset. Määritä kulmien α ja β suuruudet.

Kun suorat a ja b ovat yhdensuuntaiset, kuvasta voidaan päätellä, että kulma α ja β muodostavat ristikulma toistensa kanssa.
Jolloin α=β
Kulma β' on kulma β:n toinen ristikulma, joka on samana 159° asteen kulman vieruskulma.
b)

Ei, koska niiden kahden kulman summa ei ole 180.
c)


Suorat a ja b ovat yhdensuuntaiset. Määritä kulmien α ja β suuruudet.
Kun suorat a ja b ovat yhdensuuntaiset, kuvasta voidaan päätellä, että kulma α ja β muodostavat ristikulma toistensa kanssa.
Jolloin α=β
Kulma β' on kulma β:n toinen ristikulma, joka on samana 159° asteen kulman vieruskulma.
b)
Ei, koska niiden kahden kulman summa ei ole 180.
c)