1.2 Valosähköilmiö
Valosähköilmiö
Sähkömagneettisen säteilyn absorboituessa aineeseen säteily luovuttaa siihen energiaa. Koemme tämän ilmiön, kun auringonvalo lämmittää meitä. Sähkömagneettisen säteilyn absorptiossa kuitenkin havaitaan piirteitä, jotka poikkeavat mekaaniselle aaltoliikkeelle tyypillisestä käyttäytymisestä. Varhaisimpia tunnettuja esimerkkejä poikkeavuudesta on valosähköilmiö. Valosähköilmiössä säteilyn energia irrottaa elektroneja – "valosähköä" – metallin pinnasta. Ilmiötä demonstroidaan alla olevalla videolla.
Videolla eboniittisauvaan kerääntyy hankauksessa ylimääräisiä elektroneja. Kosketettaessa sinkkilevyä elektronit siirtyvät sauvasta levyyn. Levyyn kiinnitetty elektroskooppi ilmaisee sen varautumisen. Elektronit sitoutuvat metallihilaan tietyn suuruisella energialla, jota kutsutaan irrotustyöksi. On luontevaa olettaa, että valon siirtämä energia voi aiheuttaa elektronien irtoamisen metallista.
Valon aaltomallin kannalta tilannetta voi tarkastella seuraavasti:
- Valon intensiteetti ilmaisee säteilyn tehon pinta-alayksikköä kohden. Teho taas ilmaisee siirtyvän energian aikayksikköä kohden. Metallin vastaanottaman energian voidaan siis odottaa noudattavan kaavaa [[$ E= Pt =IAt $]].
- Tämän mukaan elektroneja irtoaa, kun ne ovat vastaanottaneet tarpeeksi paljon energiaa.
- Tarpeeksi suuri energia saavutetaan riittävän ajan kuluessa, oli valonlähde millainen tahansa.
Elektronit eivät kuitenkaan irtoa näkyvän valon vaikutuksesta pitkänkään ajan kuluessa. Myöskään näkyvän valon kirkkauden eli intensiteetin lisääminen ei muuta tilannetta. Sen sijaan UV-valo irroittaa elektronit ja purkaa varauksen. Tämä yksinkertainen havainto paljastaa valon absorptiosta piirteitä, joita on vaikea selittää aaltomallin perusteella.
Ilmiö on selitettävissä seuraavilla seikoilla:
- Sähkömagneettinen säteily koostuu energiapaketeista, kvanteista, joiden energia on sitä suurempi, mitä suurempi on säteilyn taajuus.
- Säteily absorboituu ja emittoituu kokonaisina kvantteina.
- Säteilyn kvantin absorboituessa metalliin sen energia siirtyy kokonaisuudessaan yhdelle elektronille.
Näiden seikkojen myötä valosähköilmiö tulee ymmärrettäväksi. Näkyvän valon taajuus on niin pieni, että sen kvantin energia ei riitä irrottamaan elektroneja. Intensiteetin lisääminen kasvattaa kvanttien lukumäärää, mutta yksittäisen kvantin energia ei kasva. Sen sijaan UV-valon kvanttien energia riittää elektronien irrottamiseen.
Yllä esitetyt kvanttimallin postulaatit ovat peräisin Albert Einsteinilta (1879–1955). Hän sovelsi valosähköilmiöön Max Planckin jo aiemmin esittämää hypoteesia säteilyn kvanteista. Einstein julkaisi selityksensä ilmiölle vuonna 1905 ja hänelle myönnettiin kyseisen työn nojalla fysiikan Nobelin palkinto vuonna 1921. Valosähköilmiöllä on suuri historiallinen merkitys, sillä se edustaa klassisen fysiikan murrosta moderniksi fysiikaksi sekä kvanttifysiikan alkua.
Valosähköilmiön mallintaminen
Valosähköilmiötä voidaan tarkastella edellä esitetyn kvanttihypoteesin sekä energian säilymislain näkökulmasta. Säteily luovuttaa metallille energiaa yksittäisinä kvantteina. Jos taajuus on pieni, kvanttien energia on pieni, eikä elektroneja irtoa. Suuremmalla taajuudella kvanttien energia on suurempi, jolloin elektroneja irtoaa. Rajataajuus, jolla elektroneja alkaa irrota, on eri metalleilla eri suuruinen. Rajataajuudella kvanttien energia on yhtä suuri kuin metallille ominainen irrotustyö, W0. Mikäli säteilyn taajuus on tätä suurempi, osa kvanttien energiasta muuntuu irtoavien elektronien liike-energiaksi EK.
Valosähköilmiö eri taajuuksilla. 1: Matalataajuuksinen säteily ei synnytä valosähköilmiötä. 2: Rajataajuudella elektroneja irtoaa. 3: Suurella taajuudella irtoaa elektroneja, joilla on liike-energiaa.
Energian säilyminen valosähköilmiössä voidaan ilmaista seuraavalla yhtälöllä:
[[$ \quad E_{\text{kvantti}}=W_0 +E_{\text{k}} $]]
Kvantin energia siis muuttuu irrotustyöksi ja elektronien liike-energiaksi. Järjestellään yhtälö uudelleen, jolloin saadaan
[[$ \quad E_\text{k}=E_{\text{kvantti}}-W_0 $]].
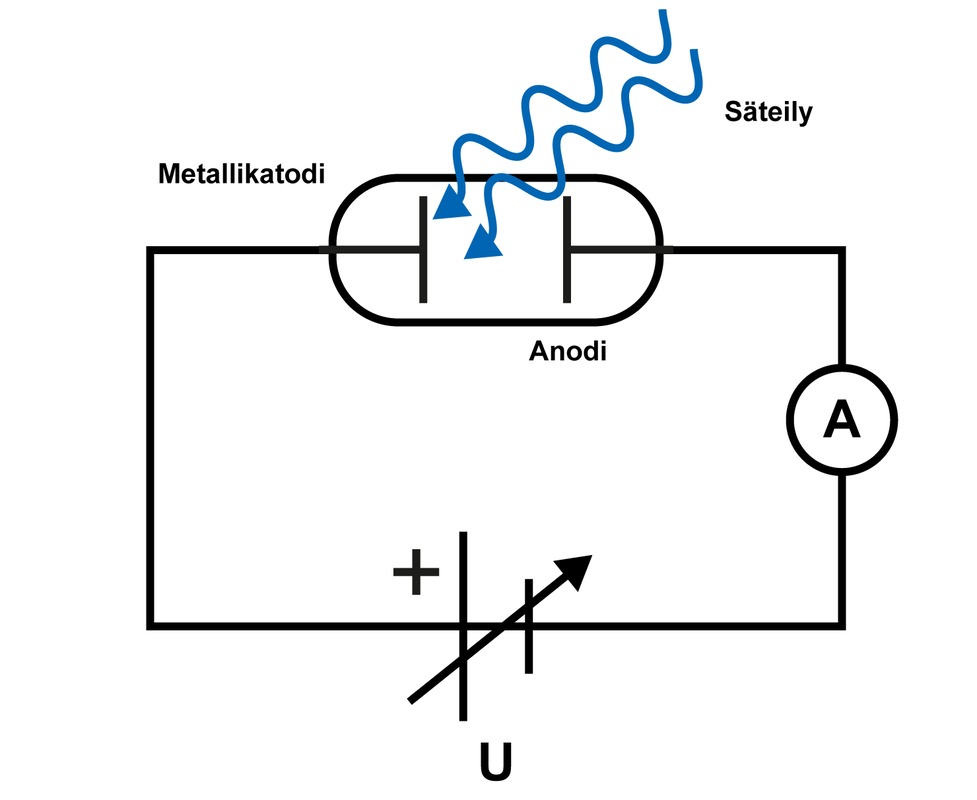Yllä esitetyn yhtälön todentaminen on mahdollista mittalaitteistolla, jossa metallilevyyn kohdistetaan valoa ja irtoavien elektronien energia voidaan mitata. Tähän soveltuva kytkentä on esitetty viereisessä kuvassa. Katodi ja anodi on sijoitettu tyhjiöputkeen ja irtoavat elektronit ilmenevät sähkövirtana piirissä. Sähkövirta saadaan lakkaamaan kytkemälle sille vastakkaissuuntainen pysäytysjännite U anodin ja katodin välille. Tällöin sähkökenttä tekee työtä elektronien liikkeen pysäyttämiseksi. Sähkökentän tekemä työ on
[[$ \quad W=Fs=QEs=QU $]]
Mittauksessa pysäytysjännite säädetään sellaiseksi, että sähkövirta piirissä lakkaa. Pysäytysjännitteen ollessa U on siis irtoavien elektronien suurin energia QU, jossa Q on elektronin varaus eli alkeisvaraus. Kun alkeisvarausta merkitään tunnuksella e, saadaan elektronien energia yksikössä eV (elektronivoltti).
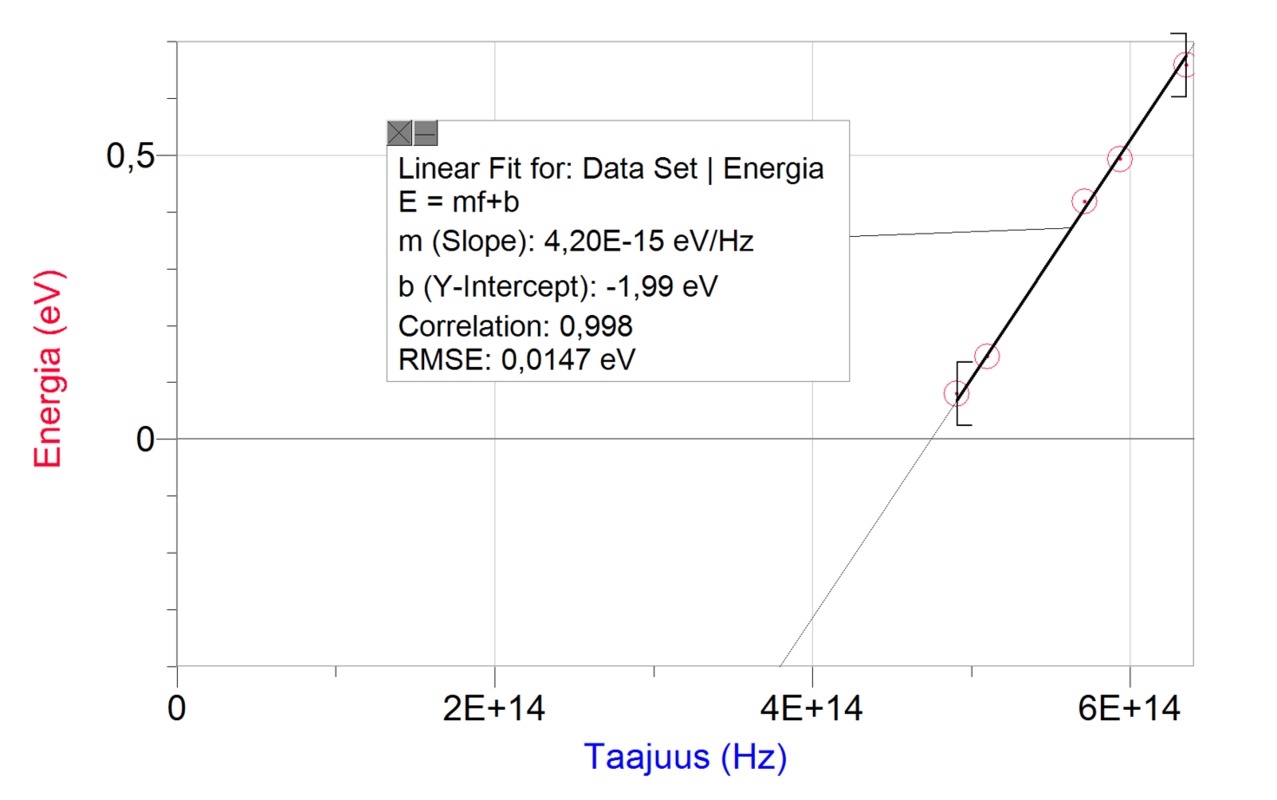
Nyt on mahdollista tutkia kvanttien energian riippuvuutta säteilyn taajuudesta. Kohdistetaan katodiin säteilyä eri taajuuksilla ja mitataan irtoavien elektronien suurin liike-energia. Kun rajataajuus on ylitetty, elektronien liike-energian havaitaan kasvavan taajuuden kasvaessa. Erästä metallia tutkittaessa havaittiin elektronien suurimman liike-energian ja valon taajuuden välillä alla olevan kuvaajan mukainen riippuvuus.
[[$ \quad E_{\text{kvantti}}= \textrm{vakio}\cdot \textrm{taajuus} $]]
Mallinnetun suoran yhtälö on kokonaisuudessaan
[[$ \quad E_\text{k}=hf-W_0 $]].
Verrannollisuuskerrointa kvantin energian ja taajuuden välillä kutsutaan Planckin vakioksi, h. Planckin vakio on suoran kulmakerroin, joka tehdyssä mittauksessa on noin [[$ 4,2 \cdot 10^{-15} \text { eVs} $]]. Metallin irrotustyö W0 = 2,0 eV saadaan suoran ja energia-akselin leikkauskohdasta, mitä ilmaisee yhtälön vakiotermi. Irrotustyö on metallille ominainen vakio.
Sähkömagneettisen säteilyn kvantit
Sähkömagneettisen säteilyn energia esiintyy paketteina, joita kutsutaan kvanteiksi. Säteily absorboituu tai emittoituu yksi kvantti kerrallaan.
Kvantin energia E on suoraan verrannnollinen säteilyn taajuuteen f:
[[$ \quad E=hf $]]
Tässä h on Planckin vakio, [[$ h=6,62606957 \cdot 10^{-34} \text{ Js}=4,13566751 \cdot 10^{-15} \text{ eVs} $]]
Energia valosähköilmiössä
Valosähköilmiössä sähkömagneettisen säteilyn kvantti luovuttaa energiansa metallin elektronille. Osa energiasta kuluu irrotustyöhön W0. Jäljelle jäävä energia muuttuu elektronin liike-energiaksi Ek:
[[$ \quad E_\text{kvantti}=E_\text{k}+W_0$]]
Yhdistämällä tähän kvantin energian kaava [[$ E=hf $]] saadaan
[[$ \quad E_\text{k}=hf-W_0 $]]
Tässä h on Planckin vakio, [[$ h=6,62606957 \cdot 10^{-34} \text{ Js}=4,13566751 \cdot 10^{-15} \text{ eVs}$]].
Huomaa, että tämä kaava tulee perustella energiaperiaatteen näkökulmasta joka kerta kaavaa käytettäessä.
Aurinkokennon toiminta perustuu valosähköilmiöön.
Energian yksiköt ja kvantit
Energian perusyksikkö joule (J) on varsin suuri yksikkö säteilykvanttien energioihin nähden. Usein on käytännöllisempää käyttää energian yksikkönä elektronivolttia (eV). Elektronivoltti on energia, jonka elektroni saa kulkiessaan yhden voltin kiihdyttävän jännitteen yli. Tämä perustuu sähkökentän tekemän työn lausekkeeseen, joka on [[$ W=QU $]]. Elektronin sähkövaraus on alkeisvaraus e, joten työn yksiköksi saadaan eV. Varaukseltaan yhtä suuri protoni saisi vastaavassa tilanteessa myös energian 1 eV.
Joulen ja elektronivoltin välinen muuntokerroin on alkeisvarauksen lukuarvo coulombeissa, eli niiden välillä pätee yhtälö
[[$ \quad 1 \text{ eV} = 1,602176462 \cdot 10^{-19} \text{ J} $]]
Kvantin energia voidaan laskea elektronivoltteina tai jouleina. Planckin vakion yksikkö valitaan halutun energian yksikön mukaisesti. Voidaan siis laskea esimerkiksi taajuudeltaan 1,4 PHz:n säteilyn kvantin energia seuraavasti:
[[$ \quad E=hf=6,62606957 \cdot 10^{-34} \text{ Js}\cdot 1,4 \cdot 10^{15}\text{ Hz} \approx 9,3 \cdot 10^{-19}\text{ J} $]]
tai
[[$ \quad E=hf=4,13566751 \cdot 10^{-15} \text{ eVs}\cdot 1,4 \cdot 10^{15}\text{ Hz} \approx 5,8\text{ eV} $]]
Metallien irrotustyöt ilmaistaan tavallisesti elektronivoltteina, ja se on käytännöllinen yksikkö valosähköisen ilmiön tarkasteluun. Näin on myös myöhempien lukujen atomitason ilmiöitä mallinnettaessa. Joule-yksikön käyttö on kuitenkin tarpeen, jos esimerkiksi halutaan ratkaista elektronin nopeus v kun tiedetään sen liike-energia EK seuraavasti:
[[$ \quad E_k=\dfrac{1}{2}mv^2 \Rightarrow v=\sqrt{\dfrac {2E_k}{m}} $]]
Jotta nopeus saataisiin SI-järjestelmän perusyksikössä m/s, tulee kaavaan sijoittaa energia jouleina ja massa kilogrammoina.
Esimerkkejä
Esimerkki 1
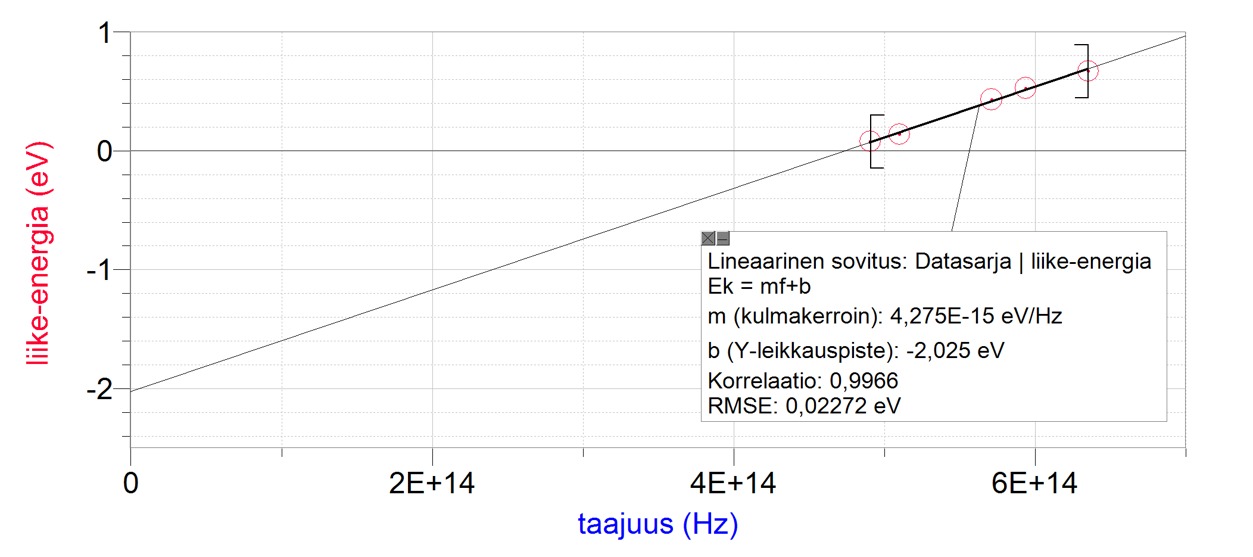
Metalliin kohdistettiin valoa, jonka taajuutta muuteltiin. Valon irrottamien elektronien suurimmat liike-energiat mitattiin. Liike-energian riippuvuutta säteilyn taajuudesta mallinnettiin ohessa esitetyllä suoralla.
a) Perustele lineaarisen mallin yhtälö.
b) Määritä mallin perusteella Planckin vakio ja metallin irrotustyö. Päättele, mikä metalli voisi olla kyseessä.
Esimerkki 2
Valosähköilmiötä tutkittiin kohdistamalla sinkkilevyyn ultraviolettivaloa. Irronneiden elektronien synnyttämä sähkövirta saatiin lakkaamaan 0,98 V:n pysäytysjännitteellä. Kuinka suuri oli valon aallonpituus?
Esimerkki 3
Valo, jonka aallonpituus on 614 nm, osuu valokennoon. Tällöin tarvitaan 0,29 V:n pysäytysjännite estämään katodilta irronneiden elektronien pääsy anodille. Kuinka suuri pysäytysjännite tarvitaan, jos valon aallonpituus on 468 nm?