Kurssiin liittyviä asioita
Kurssin suorittaminen
1. Palautettavat tehtävät 35p.
Palautettavia tehtäviä annetaan 1-2/oppitunti ja ne arvioidaan asteikolla 0-4p. Lasketaan pistekertymä ja suhteutetaan tuohon 35 pisteeseen.
2. Kokeelliset mittaukset raportteineen 35p.
Raportit ovat kukin 6-10 pisteen arvoisia. valitse itse, miten keräät pisteet kasaan. Palautus Moodleen.
3. Kurssikoe 85p.
4. Itsearvio 5p.
Yhteensä 160p. Kurssin läpaisyyn vaaditaan kokeesta vähintään 25p ja kaksi kokeellista mittausta palautettuna.
Aikataulu ja palautettavat tehtävät
| Päivämäärä | Aihe | Tehtävät | Palautettavat tehtävät |
|---|---|---|---|
| ke 10.8 | Luku 1.1 SM säteily ja spektri Simulaatio spektreistä |
101,102, 104 | 102(2), 151(2) |
| pe 12.8 | Luku 1.2 Valosähköilmiö. Esim teht. 154 | 108, 109, 111 | 108(2) tai 109(2) ja 111(2) |
| ma 15.8 | Työt 1 ja 2 Spektrien mittaus ja tulkinta (6+10p) | Mittausohje ja data Moodlessa | Mittausraporttien palautus Moodleen ma 22.8 mennessä |
| ke 17.8 | Luku 2.1 Aaltohiukkasdualismi: de Broglie. Video1 Video2 (Juha) | 202, 204 | 202(2), 204 (3) |
| pe 19.8 | Luku 3.1 Historiallisia atomimalleja. Bohrin vetyatomimalli. Viivaspektrien synty. | 304 ja 307 | 304 (2), 307 (3) |
| ma 22.8 | Luku 3.1 ja 3.2 atomin energiatasot. kertaus viivaspektrien synnystä. Purkausputkisimulaatio Vetyatomin simulaatio Kokeellinen mittaus ja sen raportointi. Ohessa raporttiohje ja mittausdatat: Kaasujen viivaspektrien analyysi.pdf Vedyn spektri.cmbl Heliumin spektri.cmbl vedyn ja heliumin spektrit.jpg |
Työ 3. emissiospektrejä (10p) | Työraportin palautus Moodleen ma 29.8 mennessä |
| ke 24.8 | Luku 3.3 Teknisiä sovelluksia ja luonnonilmiöitä Laserin toimintaperiaate Laserlabra Laser ja eriväriset ilmapallot |
308, 310 (palautus oppitunnilla), 355, 357, 358 | Kaksi tehtävistä 355 (3), 357 (3), 358 (3) |
| pe 26.8 | Luku 5.3 Röntgensäteily ja sen spektri Samulin tiedekanava |
512 (palautus tunnilla, 2p), 516 Katso video röntgendiffraktio |
516 (3) |
| ma 29.8 | Luku 4.1Atomiydin. Tunti luokassa 3057 | 401(palautus tunnilla, 2p), 402, 404 | 402 (3), 404 (3) |
| ke 31.8 | Luvut 4.2 ja 4.3: Radioaktiiviset hajoamisreaktiot. Energia alfahajoamisessa. | 405, 409 | 405 (2), 409 (3) |
| pe 2.9 | Luvut 4.2 ja 4.3: Beta-hajoaminen, elektronisieppaus | 407 (tunnilla palautus,3p), 410, 411 | 410 (3), 411 (3) |
| ma 5.9 | Luku 4.4 Hajoamislaki. HUOM! Tunti itsenäistä työskentelyä. | 412, 413, 414 | Kaksi tehtävää joukosta 412, 413, 414 (3p/teht.) |
| ke 7.9 | Luku 4.4, soveltavat tehtävät, gammasäteily. FY7 käsitekartta.pdf Säteilyturvallisuudesta.pdf |
458 (tunnilla, 2p), 456, 457 | 456 (4), 457(4) |
| pe 9.9 | Kokeelliset työt 4 ja 5 (8+8p) | Työ 4. Säteilylähteiden tunnistaminen Työ 5. Barium-isotooppi |
Työraporttien palautus Moodleen pe 16.9 mennessä |
| ma 12.9 | Kokeellinen työ 6 (6p) | Työ 6 Gammasäteilyn vaimeneminen | Työraportin 6 palautus Moodleen ma 19.9 mennessä. 553 (2), 555 (2) |
| ke 14.9 | Luku 5.1 Ydinvoima Simulaatio fissiosta Luku 5.3 Radiohoiiliajoitus |
501, 560 (3) tunnilla | 503 (3), 505 (2p) |
| pe 16.9 | Työraporttien kirjoitusta | ||
| ma 19.9 | Luku 6.1 Fysiikan standardimalli Cern standardimalli LHC toimintaperiaate Luku 6.2 Kosmologiaa |
601, 650 | |
| ti 20.9 | Kurssikoe 9-12 (-13) |
Esim. beetahajoaminen
Esim. gammasäteily
Teht. 501
355 ratkaisu
Atomien energiatasot ilmoitetaan joissain lähteissä niin, että viritystilan ero perustilaan ilmaistaan pituusyksikön avulla. Esimerkiksi vedyn ensimmäinen viritystila voidaan ilmaista 82258 cm-1. Päättele mihin tämä perustuu ja ilmaise samalla tavalla vedyn toisen viritystilan energia.
Ratkaisu
Viritystilan ero perustilaan liittyy siirtymässä vapautuvan fotonin aallonpituuteen kaavan [[$E=\dfrac{hc}{\lambda}$]] mukaisesti. Jos [[$hc$]] sisällytetään energian yksikköön, arvoksi jää [[$\dfrac{1}{\lambda}$]]. Tällä on oikea yksikkö. Tarkastetaan, onko lukuarvo oikea. Ensimmäisen viritystilan purkautuessa vapautuu fotoni, jonka energia on
[[$E=13{,}6\text{ eV}-13{,}6\text{ eV}\cdot\dfrac{1}{4}=10{,}2\text{ eV}$]]
Tämä vastaa aallonpituutta
[[$\lambda=\dfrac{hc}{E}=\dfrac{1\,240\text{ eV nm}}{10{,}2\text{ eV}}=121{,}5686\dots\text{ nm}\approx 1{,}21569\cdot 10^{-5}\text{ cm}$]]
Tällöin energiaksi halutuissa yksiköissä saadaan
[[$E\text{ 1/hc}=\dfrac{1}{1{,}21569\cdot 10^{-5}\text{ cm}}=82\,258{,}0\dots\text{1/cm}\approx 82\,258\text{ 1/cm}$]]
Tulos on oikea, eli logiikka on selvinnyt. Kun valitaan [[$hc=1$]], voidaan käyttää yksikönmuunnosta
[[$10{,}2\text{ eV}=82\,258\text{ 1/cm}$]]
Näin toisen viritystilan energiaksi saadaan
[[$E=\dfrac{13{,}6\text{ eV}-13{,}6\text{ eV}\cdot\dfrac{1}{9}}{10{,}2\text{ eV}}\cdot 82\,258\text{ 1/cm}=97\,490{,}9\dots\text{1/cm}\approx 97\,491\text{ 1/cm}$]]
357 ratkaisu
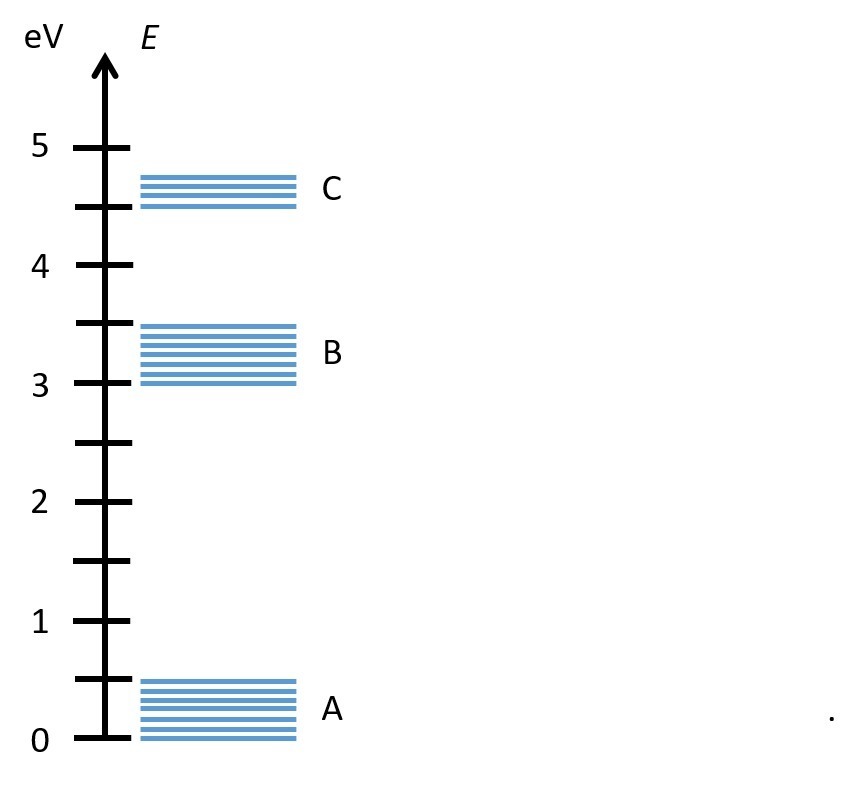Kvartsikiteen rakennepoikkeamien energiatiloja voidaan mallintaa kuvassa esitetyllä tavalla lähekkäisten tilojen ryhminä. Ryhmiä kutsutaan tässä energiavyöhykkeiksi. Vyöhykettä A kutsutaan perustilojen vyöhykkeeksi. Kun kvartsikide ottaa vastaan energiaa, se voi virittyä kaikille kuvassa näkyville energiavyöhykkeille, mutta kun se luovuttaa energiaa, se palautuu aina vyöhykkeelle A.
a) Millä aallonpituuksilla kvartsikide absorboi ja emittoi säteilyä?
b) Miten energiatilojen ryhmittyminen energiavyöhykkeiksi näkyy kvartsikiteen emittoiman säteilyn spektrissä?
Ratkaisu
a) Säteilykvantin energian ja aallopituuden välinen yhteys
[[$ E=\dfrac{hc}{\lambda}\\
\lambda = \dfrac{hc}{E} $]]
Emittoituneen fotonin aallonpituus vastaa energiatilojen välistä energiaeroa.
[[$ \lambda = \dfrac{hc}{\Delta E} $]]
Lasketaan energiaerot energiatasokaaviosta, kun siirtymä tapahtuu vyöhykkeeltä B ja C vyöhykkeelle A. Energiaeron laskemiseksi on huomioita vyöhykkeiden suurin ja pienin energiaero.
Siirtymä vyöhykkeeltä B vyökkyylle A
[[$ \Delta E_{B->A,max}=3,5 \ \mathrm{eV}-0 \ \mathrm{eV}=3,5 \ \mathrm{eV}\\
\Delta E_{B->A,min}=3,0 \ \mathrm{eV}-0,5 \ \mathrm{eV}=2,5 \ \mathrm{eV}$]]
Aallonpituudet, joilla fotoneja emittoituu
[[$ h= 4,135667662 \cdot 10^{-15} \ \mathrm{eVs}\\
c=2,99792458 \cdot 10^8 \ \mathrm{\frac{m}{s}} $]]
Emittoituneiden fotonien aallonpituudet ovat
[[$ \lambda_{B->A,max}=3,5424056\cdot 10^{-7} \ \mathrm{m}\approx 354 \ \mathrm{nm}\\
\lambda_{B->A,min}=4,9593679\cdot 10^{-7} \ \mathrm{m}\approx 496 \ \mathrm{nm} $]]
Aallonpituusalue on 350 nm - 500 nm.
Siirtymä vyöhykkeeltä C vyökkyylle A
[[$ \Delta E_{C->A,max}=4,75 \ \mathrm{eV}-0 \ \mathrm{eV}=4,75 \ \mathrm{eV}\\
\Delta E_{C->A,min}=4,5 \ \mathrm{eV}-0,5 \ \mathrm{eV}=4,0 \ \mathrm{eV}$]]
Aallonpituudet, joilla fotoneja emittoituu
[[$ h= 4,135667662 \cdot 10^{-15} \ \mathrm{eVs}\\
c=2,99792458 \cdot 10^8 \ \mathrm{\frac{m}{s}} $]]
Emittoituneiden fotonien aallonpituudet ovat
[[$ \lambda_{C->A,max}=2,6101936\cdot 10^{-7} \ \mathrm{m}\approx 261 \ \mathrm{nm}\\
\lambda_{C->A,min}=3,0996049\cdot 10^{-7} \ \mathrm{m}\approx 310 \ \mathrm{nm} $]]
Aallonpituusalue on 260 nm - 310 nm.
Absorptio taphatuu samoilla aallonpituusväleillä kuin emissio. Tämä lisäksi absorptio voi tapahtua vyöhykkeeltä B vyökkeelle C.
Siirtymä vyöhykkeeltä B vyökkyylle C
[[$ \Delta E_{B->C,max}=4,75 \ \mathrm{eV}-3,0 \ \mathrm{eV}=1,75 \ \mathrm{eV}\\
\Delta E_{B->C,min}=4,5 \ \mathrm{eV}-3,5 \ \mathrm{eV}=1,0 \ \mathrm{eV}$]]
Aallonpituudet, joilla fotoneja absorboituu
[[$ h= 4,135667662 \cdot 10^{-15} \ \mathrm{eVs}\\
c=2,99792458 \cdot 10^8 \ \mathrm{\frac{m}{s}} $]]
Absorboituneiden fotonien aallonpituudet ovat
[[$ \lambda_{B->A,max}=7,0848113\cdot 10^{-7} \ \mathrm{m}\approx 708 \ \mathrm{nm}\\
\lambda_{B->A,min}=1,239842\cdot 10^{-6} \ \mathrm{m}\approx 1240 \ \mathrm{nm}$]]
Aallonpituusalue on 710 nm - 1240 nm.
b) Kvartsikiteen emissiospektrissä ei havaita yksittäisiä siirtymiä vastaavia spektriviivoja, vaan paksumpi emissiovyöhyke. Vyöhykkeitä on kaksi kappaletta, edellä lasketut 350 nm - 500 nm (vyöhykkeeltä B vyöhykkeelle A) ja 260 nm - 310 nm (vyöhykkeeltä C vyöhykkeelle A).
358 ratkaisu
a) Laserin toimintaperiaate ja laserin valon tärkeimmät ominaisuudet.
b) Oheisessa kuvassa on esitetty argonlaserin yksinkertaisettu energiatasokaavio. Kuvaan on merkitty lasersiirtymät a ja b. Laske siirtymiä vastaavat aallonpituudet. Minkä väristä on näissä siirtymissä syntyvä valo?
Ratkaisu
a) Laservalon tuotto perustuu kaasun viritystilojen purkaantumiseen. Laserputkessa on kaasua, jota viritetään sähkövirralla. Viritystilat eivät purkaannu välittömästi (viritystilan kesto luokkaa millisekunti). Kun jokin atomin viritystila purkaantuu, emittoituu fotoni. Fotonin energia on yhtä suuri kuin energiatilojen välinen energiaero. Fotoni etenee putkessa, jossa on edelleen virittyneitä atomeja. Fotoni voi ohittaessaan virittyneen atomin purkaa sen. Myös uuden fotonin energia on sama kuin virittyneessä tilassa olevan atomin energiatilojen välinen energiaero. Tällä tavoin syntyy fotoneja, jotka voivat edelleen purkaa viritystilassa olevia atomeja. Tapahtumaa kutsutaan stimuloiduksi emissioksi.
Laserputken päissä on peilit. Toinen peileistä on osittain heijastava ja laskee läpi noin 1-2 prosenttia fotoneista. Nämä peilin läpäisseet fotonit muodostavat valon, joka havaitaan lasersäteenä. Koska peili laskee läpi vain tietystä suunnasta tulevia fotoneja, syntyy kapea fotonien keila eli lasersäde. Peilistä heijastuneet fotonit risteilevät putkessa ja voivat edelleen purkaa virittyneitä atomeja.
Stimuloidussa emissiossa syntyvien fotonien energia on yhtä suuri kuin kaasun energiatilojen välinen energiaero. Täten kaikilla fotoneilla sama energia ja sama aallonpituus säteilykvantin energian ja aallonpituuden välisen yhteyden perusteella.
[[$ \Delta E=\dfrac{hc}{\lambda} $]]
Stimuloitu emissio tuottaa laservaloa, jonka fotoneilla on sama vaihe.
b) Säteilykvantin energian ja aallopituuden välinen yhteys
[[$ E=\dfrac{hc}{\lambda}\\
\lambda = \dfrac{hc}{E} $]]
Emittoituneen fotonin aallonpituus vastaa energiatilojen välistä energiaeroa.
[[$ \lambda = \dfrac{hc}{\Delta E} $]]
Lasketaan energiaerot energiatasokaaviosta.
[[$ \Delta E_a=35,9 \ \mathrm{eV}-33,5 \ \mathrm{eV}=2,4 \ \mathrm{eV}\\
\Delta E_b=36,05 \ \mathrm{eV}-33,5 \ \mathrm{eV}=2,55 \ \mathrm{eV} $]]
[[$ h= 4,135667662 \cdot 10^{-15} \ \mathrm{eVs}\\
c=2,99792458 \cdot 10^8 \ \mathrm{\frac{m}{s}} $]]
Emittoituneiden fotonien aallonpituudet ovat
[[$ \lambda_a=5,1660082\cdot 10^{-7} \ \mathrm{m}\approx 517 \ \mathrm{nm}\\
\lambda_b=4,8621254\cdot 10^{-7} \ \mathrm{m}\approx 486 \ \mathrm{nm}$]]
Aallonpituus 517 nm on syaanin ja vihreän värin rajalla. Aallonpituus 486 on sinisen värin alueella. Syntyvä valo on sinivihreää.