Valosähköilmiötä voidaan tarkastella edellä esitetyn kvanttihypoteesin sekä energian säilymislain näkökulmasta. Säteily luovuttaa metallille energiaa yksittäisinä kvantteina. Jos taajuus on pieni, kvanttien energia on pieni, eikä elektroneja irtoa. Suuremmalla taajuudella kvanttien energia on suurempi, jolloin elektroneja irtoaa. Rajataajuus, jolla elektroneja alkaa irrota, on eri metalleilla eri suuruinen. Rajataajuudella kvanttien energia on yhtä suuri kuin metallille ominainen irrotustyö, W₀. Mikäli säteilyn taajuus on tätä suurempi, osa kvanttien energiasta muuntuu irtoavien elektronien liike-energiaksi E_K.

Energian säilyminen valosähköilmiössä voidaan ilmaista seuraavalla yhtälöllä:

[[$ \quad E_{\text{kvantti}}=W_0 +E_{\text{k}} $]]

Kvantin energia siis muuttuu irrotustyöksi ja elektronien liike-energiaksi. Järjestellään yhtälö uudelleen, jolloin saadaan

[[$ \quad E_\text{k}=E_{\text{kvantti}}-W_0 $]].

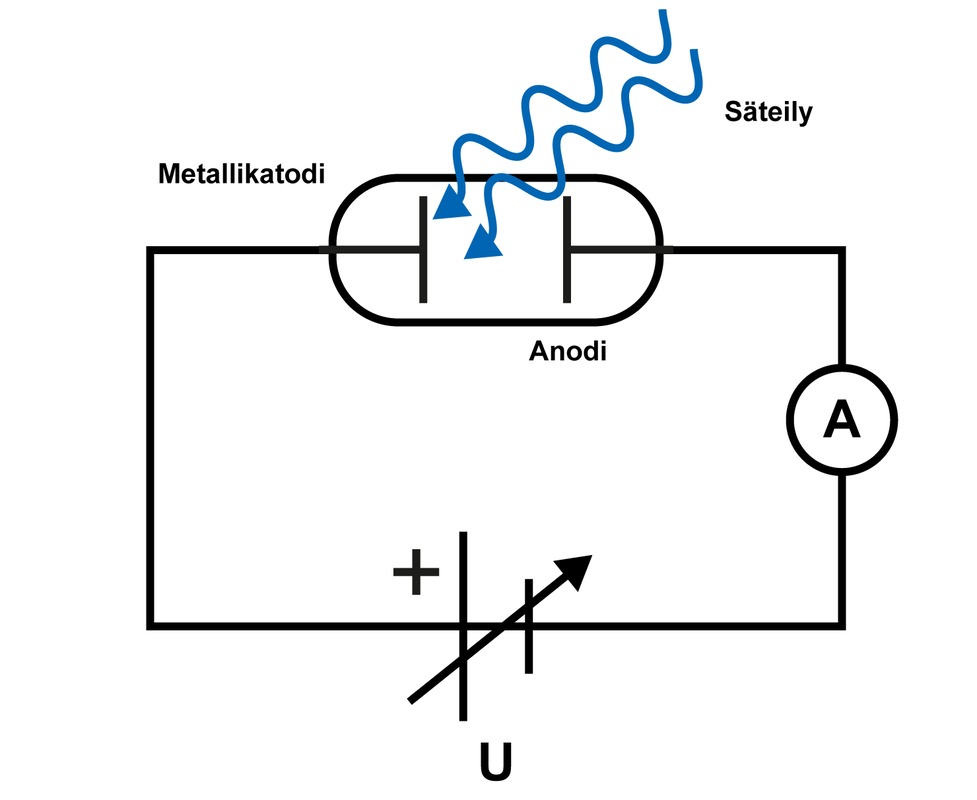Yllä esitetyn yhtälön todentaminen on mahdollista mittalaitteistolla, jossa metallilevyyn kohdistetaan valoa ja irtoavien elektronien energia voidaan mitata. Tähän soveltuva kytkentä on esitetty viereisessä kuvassa. Katodi ja anodi on sijoitettu tyhjiöputkeen ja irtoavat elektronit ilmenevät sähkövirtana piirissä. Sähkövirta saadaan lakkaamaan kytkemälle sille vastakkaissuuntainen pysäytysjännite U anodin ja katodin välille. Tällöin sähkökenttä tekee työtä elektronien liikkeen pysäyttämiseksi. Sähkökentän tekemä työ on

[[$ \quad W=Fs=QEs=QU $]]

Mittauksessa pysäytysjännite säädetään sellaiseksi, että sähkövirta piirissä lakkaa. Pysäytysjännitteen ollessa U on siis irtoavien elektronien suurin energia QU, jossa Q on elektronin varaus eli alkeisvaraus. Kun alkeisvarausta merkitään tunnuksella e, saadaan elektronien energia yksikössä eV (elektronivoltti).

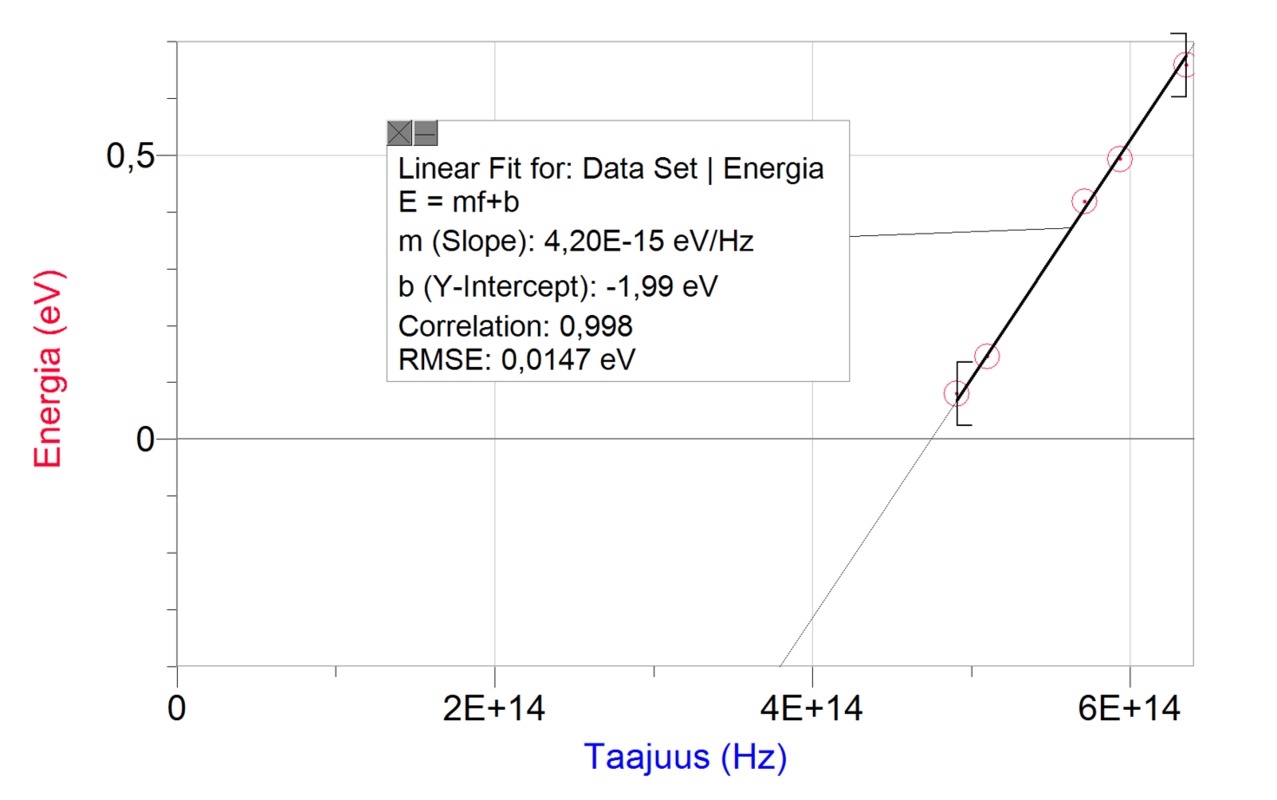
Nyt on mahdollista tutkia kvanttien energian riippuvuutta säteilyn taajuudesta. Kohdistetaan katodiin säteilyä eri taajuuksilla ja mitataan irtoavien elektronien suurin liike-energia. Kun rajataajuus on ylitetty, elektronien liike-energian havaitaan kasvavan taajuuden kasvaessa. Erästä metallia tutkittaessa havaittiin elektronien suurimman liike-energian ja valon taajuuden välillä alla olevan kuvaajan mukainen riippuvuus.

[[$ \quad E_{\text{kvantti}}= \textrm{vakio}\cdot \textrm{taajuus} $]]

Mallinnetun suoran yhtälö on kokonaisuudessaan

[[$ \quad E_\text{k}=hf-W_0 $]].

Verrannollisuuskerrointa kvantin energian ja taajuuden välillä kutsutaan Planckin vakioksi, h. Planckin vakio on suoran kulmakerroin, joka tehdyssä mittauksessa on noin [[$ 4,2 \cdot 10^{-15} \text { eVs} $]]​. Metallin irrotustyö W₀ = 2,0 eV saadaan suoran ja energia-akselin leikkauskohdasta, mitä ilmaisee yhtälön vakiotermi. Irrotustyö on metallille ominainen vakio.

Sähkömagneettisen säteilyn kvantit

Sähkömagneettisen säteilyn energia esiintyy paketteina, joita kutsutaan kvanteiksi. Säteily absorboituu tai emittoituu yksi kvantti kerrallaan.

Kvantin energia E on suoraan verrannnollinen säteilyn taajuuteen f:

[[$ \quad E=hf $]]

Tässä h on Planckin vakio, [[$ h=6,62606957 \cdot 10^{-34} \text{ Js}=4,13566751 \cdot 10^{-15} \text{ eVs} $]]

 

Energia valosähköilmiössä

Valosähköilmiössä sähkömagneettisen säteilyn kvantti luovuttaa energiansa metallin elektronille. Osa energiasta kuluu irrotustyöhön W₀. Jäljelle jäävä energia muuttuu elektronin liike-energiaksi E_k:

[[$ \quad E_\text{kvantti}=E_\text{k}+W_0$]]

Yhdistämällä tähän kvantin energian kaava [[$ E=hf $]]​ saadaan

[[$ \quad E_\text{k}=hf-W_0 $]]

Tässä h on Planckin vakio, [[$ h=6,62606957 \cdot 10^{-34} \text{ Js}=4,13566751 \cdot 10^{-15} \text{ eVs}$]].

Huomaa, että tämä kaava tulee perustella energiaperiaatteen näkökulmasta joka kerta kaavaa käytettäessä.

Simulaatio: valosähköilmiö

Aurinkokennon toiminta perustuu valosähköilmiöön.