4.1 Ympyrän keskipistemuotoinen yhtälö
403
a)

%5Cright)%5E2%2B%5Cleft(2-1%5Cright)%5E2%7D%3D%5Csqrt%7B4%2B1%7D%3D%5Csqrt%7B5%7D)
b)
%5E2%2B%5Cleft(y-y_0%5Cright)%5E2%3Dr%5E2)
%5Cright)%5E2%2B%5Cleft(y-2%5Cright)%5E2%3D5)
c)
%5Cright)%5E2%2B%5Cleft(y-2%5Cright)%5E2%3D5)
%5Cright)%5E2%2B%5Cleft(3-2%5Cright)%5E2%3D5)

%5Cright)%5E2%2B%5Cleft(2-2%5Cright)%5E2%3D5)

b)
c)
sijoitetaan pisteet ympyrän yhtälöön
jos piste toteuttaa yhtälön, se on ympyrällä, piste B on siis ympyrä
402
401
a)
b)
c)
söös
Tehtävä 4
lasketaan pisteen (2, 1) etäisyys ympyrän keskipisteestä
%5E2%2B%5Cleft(1-%5Cleft(-1%5Cright)%5Cright)%5E2%7D%3D%5Csqrt%7B1%2B4%7D%3D%5Csqrt%7B5%7D)


etäisyys on suurempi kuin ympyrän säde, joten piste on kehän ulkopuolella
409

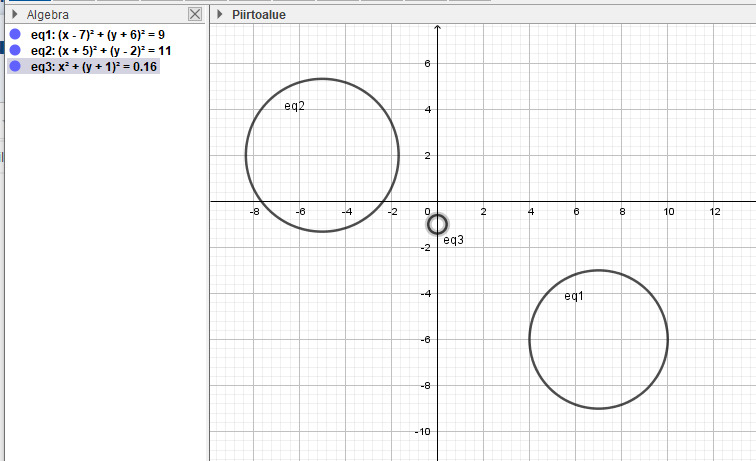
a)
ympyröiden välinen etäisyys on yhden desimaalin tarkkuudella 5,9
b)
ympyröiden välinen etäisyys on keskipisteiden välinen etäisuus josta on vähennetty ympyröiden säteet

%5Cright)%5E2%2B%5Cleft(-5-0%5Cright)%5E2%7D)


Ympyrän keskipiste on (3, -1) ja säde 2.
a) Määritä ympyrän yhtälö.
%5E2%2B%5Cleft(y-y_0%5Cright)%5E2%3Dr%5E2)

%3D%5Cleft(3%7B%2C%7D-1%5Cright))
%5E2%2B%5Cleft(y-%5Cleft(-1%5Cright)%5Cright)%5E2%3D2%5E2)
b) Onko piste (1, -1) ympyrällä?
sijoitetaan pisteen koordinaatit keskipistemuotoiseen yhtälöön
%5E2%2B%5Cleft(%5Cleft(-1%5Cright)-%5Cleft(-1%5Cright)%5Cright)%5E2%3D2%5E2)


piste on ympyrällä
sijoitetaan pisteen koordinaatit keskipistemuotoiseen yhtälöön
piste on ympyrällä
c) Selvitä miten piste (2, 1) sijaitsee ympyrään nähden. (Onko piste ympyrän kehällä, sisällä vai ulkopuolella.)
lasketaan pisteen (2, 1) etäisyys ympyrän keskipisteestä
etäisyys on suurempi kuin ympyrän säde, joten piste on kehän ulkopuolella
409

a)
ympyröiden välinen etäisyys on yhden desimaalin tarkkuudella 5,9
b)
ympyröiden välinen etäisyys on keskipisteiden välinen etäisuus josta on vähennetty ympyröiden säteet