3.3 Ratkaisukaava
Toisen asteen yhtälön ratkaisukaava
[[$$ \begin{align} ax^2+bx+c &=0 && || -c \\ ax^2+bx &=-c && || \cdot 4a \\ 4a^2x^2+4abx&=-4ac && \\ (2ax)^2+2 \cdot 2a \cdot b \cdot x&=-4ac &&||+b^2 \\ (2ax)^2 +2 \cdot 2a \cdot b \cdot x +b^2 &=b^2-4ac && || \textrm{binomin neliö} (a+b)^2=a^2+2ab+b^2\\ (2ax+b)^2&=b^2-4ac && || \textrm{otetaan neliöjuuri, ehto } b^2-4ac \geq 0 \\ 2ax+b &= \pm \sqrt{b^2-4ac} &&|| -b \\ 2ax &= -b \pm \sqrt{b^2-4ac} &&|| :2a (a \neq 0) \\ x&=\frac{-b \pm \sqrt{b^2-4ac} }{2a} \end{align}$$]]
Toisen asteen yhtälön [[$ax^2+bx+c=0$]] ratkaisut saadaan kaavasta [[$$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}, \quad \textrm{kun } a \neq 0 \textrm{ ja } b^2-4ac \geq 0$$]]
Yhtälön ratkaisuja kutsutaan yhtälön juuriksi [[$$x_1=\frac{-b - \sqrt{b^2-4ac}}{2a} \quad \textrm{ ja } x_2=\frac{-b + \sqrt{b^2-4ac}}{2a} $$]]
Nämä ratkaisut ovat polynomin [[$P(x)=ax^2+bx+c$]] nollakohtia.
Aiempien kuvaajatarkastelujen mukaan yhtälöllä voi olla kaksi, yksi tai ei yhtään erisuurta reaalista ratkaisua (vrt. luku 3.2). Kun toisen asteen yhtälö ratkaistaan ratkaisukaavan avulla, yhtälö on ensin saatettava perusmuotoon, jossa kaikki termit on siirretty vasemmalle.
Esimerkki 1
Ratkaise yhtälöt
a) [[$ x^2-4x-12=0 $]]
b) [[$x(2-x)=5$]]
Ratkaisu:
a) [[$$\begin{align} & x^2-4x-12=0 & ||\textrm{ratkaisukaava } x&=\frac{-b \pm \sqrt{b^2-4ac}}{2c}\\ \\ &\textrm{erotetaan kertoimet } a=1, b=-4, c=-12 &\\ \\ x&= \frac{-(-4) \pm\sqrt{(-4)^2 -4 \cdot1 \cdot(-12)}}{2\cdot 1} =\frac{4 \pm \sqrt{16-(-48)}}{2} & \\ & =\frac{4 \pm \sqrt{64}}{2} =\frac{4 \pm 8}{2} & \\ x&=\frac{4-8}{2}=\frac{-4}{2}=-2 \textrm{ tai } x=\frac{4+8}{2}=\frac{12}{2}=6 &\end{align} $$]]
b)[[$$\begin{align}x(2-x)&=5 & \textrm{Poistetaan sulkeet ja muutetaan perusmuotoon.} \\ 2x-x^2&=5& \textrm{Kaikki termit vasemmalle} \\ -x^2+2x-5&=0 &\textrm{ratkaisukaava}\\ x&=\frac{2 \pm \sqrt{2^2 -4 \cdot (-1) \cdot (-5)}}{2 \cdot (-1)} \\ &=\frac{2 \pm \sqrt{4-20}}{-2} \\ &=\frac{2 \pm \sqrt{-16}}{-2} & \textrm{Negatiivisesta luvusta ei voi ottaa neliöjuurta.} \\ &\textrm{Yhtälöllä ei ole ratkaisua.}& \end{align} $$]]
Vastaus:
a) [[$ x= -2 \textrm{ tai } x=6$]]
b) Yhtälöllä ei ole ratkaisua.
Jos ratkaisukaavassa neliöjuuren arvoksi ei tule kokonais- tai murtolukua, juuri on sievennettävä ja vastaus annettava tarkkana arvona sekä tarvittaessa likiarvona.
Esimerkki 2
Ratkaise yhtälöt
a) [[$\frac{1}{3}x^2-\frac{1}{9}x -\frac{1}{9}=0$]]
b) [[$4a^2-4a-11=0$]]
Ratkaisu:
a) [[$$\begin{align}&\frac{1}{3}x^2-\frac{1}{9}x-\frac{1}{9}=0 \quad | \cdot 9 \quad \textrm{yksinkertaistetaan kertoimia ennen sijoitusta}\\ &3x^2-x-1=0 &\\ x&=\frac{-(-1) \pm \sqrt{(-1)^2-4 \cdot 3 \cdot (-1)}}{2 \cdot 3} = \frac{1 \pm \sqrt{1+12}}{6} \\&=\frac{1 \pm \sqrt{13}}{6} \quad \textrm{(tarkka arvo)} \\ x &\approx -0,43 \textrm{ tai } x \approx 0,77 \end{align}$$]]
b) [[$$ \begin{align}&4a^2+4a-11=0&||\textrm{ratkaisukaavasta}\\a=&\frac{4\pm \sqrt{4^2 -4 \cdot 4 \cdot (-11)}}{2\cdot 4} \\ &=\frac{4\pm \sqrt{ 16+11 \cdot 16 }}{8}=\frac{4 \pm \sqrt{16 \cdot 12}}{8} =\frac{4 \pm 4\sqrt{4 \cdot 3}}{8}\\&=\frac{4 \pm 8\sqrt{3}}{8}=\frac{8(\frac{1}{2} \pm \sqrt{3})}{8}=\frac{1}{2} \pm \sqrt{3}\quad (a \approx -1,23 \textrm{ tai } a \approx 2,23)\end{align}$$]]
Vastaus:
a) [[$ x =\frac{1 \pm \sqrt{13}}{6} \approx -0,43 \textrm{ tai } x \approx 0,77 $]]
b) [[$ a = \frac{1}{2} \pm \sqrt{3} \approx -1,23 \textrm{ tai } a \approx 2,23 $]]
Esimerkki 3
Ratkaise luku [[$x$]] yhtälöstä [[$x^2-2ax+x-3a^2-3a=0$]].
Ratkaisu:
Luku [[$a$]] on yhtälössä vakio ja [[$x$]] muuttuja, joka ratkaistaan ratkaisukaavalla. Yhtälössä on kaksi ensimmäisen asteen termiä, joille pitää löytää yhteinen kerroin ottamalla [[$x$]] yhteiseksi tekijäksi.
[[$x^2-2ax+x-3a^2-3a = 0 \Leftrightarrow x^2+\underbrace{(-2a+1)}_{=b}x\underbrace{-3a^2-3a}_{=c}=0$]]
Sijoitetaan ratkaisukaavaan:
[[$$x=\frac{-(-2a+1)\pm \sqrt{(-2a+1)^2-4\cdot1\cdot(-3a^2-3a)}}{2 \cdot 1}=\frac{2a-1\pm \sqrt{16a^2+8a+1}}{2}$$]]
Nyt juuren alla [[$16a^2=(4a)^2$]] ja [[$8a=2\cdot 4a\cdot 1$]], joten lauseke on binomin neliö ja kaavan [[$(a+b)^2=a^2+2ab+b^2$]] avulla saadaan
[[$$x=\frac{2a-1 \pm \sqrt{(4a+1)^2}}{2} = \frac{2a-1 \pm (4a+1)}{2} \quad \text{Huomaa} \sqrt{a^2}=|a|, \text{mutta itseisarvot voi jättää pois } \pm\text{-merkin vuoksi} $$]]
[[$$ x=\frac{2a-1-(4a+1)}{2}=\frac{-2a-2}{2}=\frac{2(-a-1)}{2}=-a-1$$]] tai
[[$$ x= \frac{2a-1+4a+1}{2}=\frac{6a}{2}=3a$$]]
Vastaus: [[$x = -a-1 \text{ tai } x =3a$]]
Sovelluksia
Seuraavissa esimerkeissä käytännön tilanne johtaa toisen asteen yhtälöön.
Esimerkki 4
Suorakulmion muotoisen tontin pinta-ala on 1260 m2 ja ympärysmitta 144 m. Kuinka pitkiä ovat tontin sivut?
Ratkaisu:
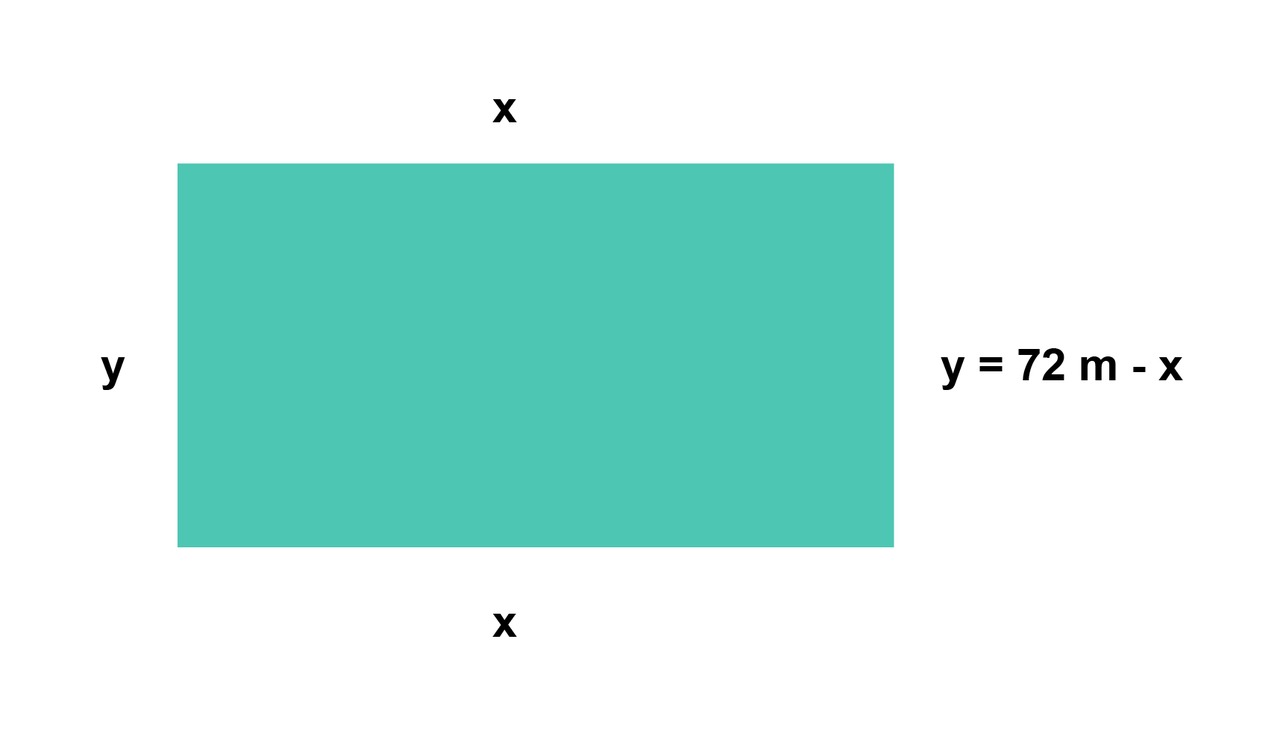
Merkitään vaakasivun pituutta muuttujalla [[$x$]]. Kahden vaakasivun pituus on [[$2x$]]. Pystysuuntaisiin sivuihin jää tällöin yhteensä [[$144-2x$]] metriä. Yksi pystysivu on näin [[$y=\frac{144-2x}{2}$]] metriä, eli sievennettynä [[$y= 72 -x$]] metriä. (Sama voidaan päätellä myös niin, että yksi vaakasivu ja pystysivu ovat yhteensä puolet ympärysmitasta, eli 72 m. Näin [[$x+y=72 \Leftrightarrow y=72-x $]].)
Pinta-ala: [[$x(72-x)=1260$]], josta normaalimuodossa [[$72x-x^2=1260 \Leftrightarrow -x^2+72x-1260=0$]]
Ratkaisukaavalla
[[$$x=\frac{-72 \pm \sqrt{72^2-4 \cdot (-1) \cdot (-1260)}}{2 \cdot (-1)} = \frac{-72 \pm \sqrt{144}}{-2} = \frac{-72 \pm 12}{-2},$$]]
josta saadaan ratkaisut
[[$$x=\frac{-60}{-2}=30 \textrm{ tai } x=\frac{-84}{-2}=42.$$]]
Jos vaakasivun pituus on [[$x=30 \textrm{ m}$]], toinen sivu on [[$72 \textrm{ m} - 30 \textrm{ m}=42 \textrm{ m}$]], joka on juuri toinen yhtälön juuri. Samoin, jos [[$x=42$]], on [[$y=30$]].
Vastaus: Sivujen pituuden ovat 42 metriä ja 30 metriä.
Esimerkki 5
Ilmaan potkaistun pallon lentorata noudatti funktiota [[$y=-0,0125x^2+0,3x$]], missä [[$x$]]-akseli kuvaa maan pintaa ja koordinaatiston yksikkönä on 1 m. Kuinka pitkälle pallo lensi vaakasuunnassa? Kuinka korkealla se kävi?
Ratkaisu:
Pallo on maan pinnalla kuvaajan nollakohdissa.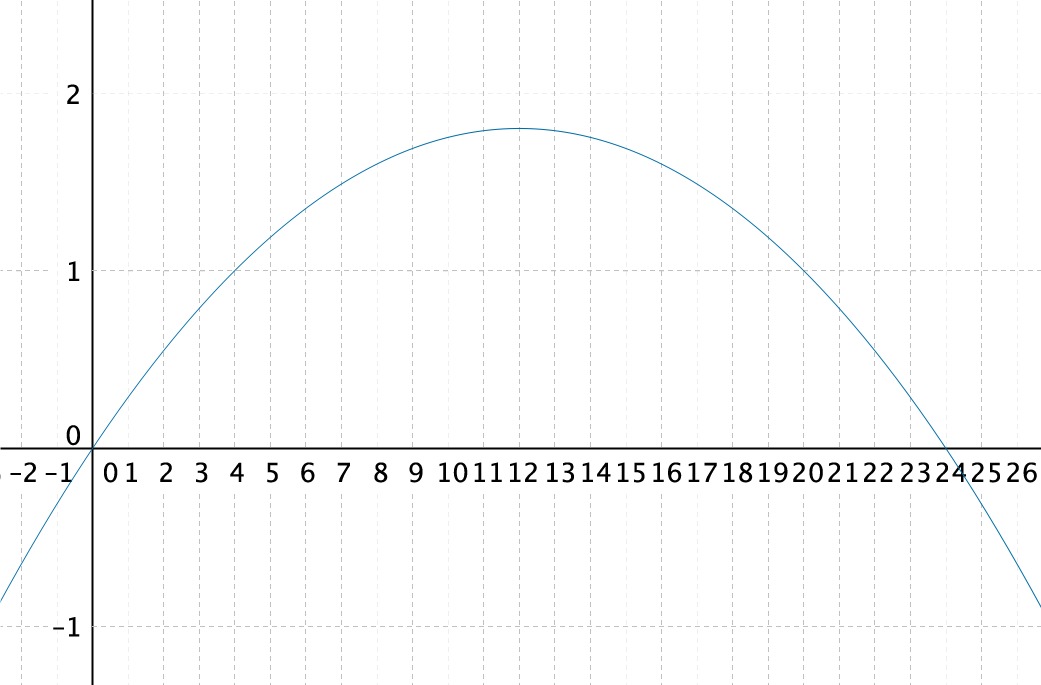
[[$y=0 \Leftrightarrow -0,0125x^2+0.3x=0 \Leftrightarrow x(-0,0125x+0,3)=0 $]]
[[$\Leftrightarrow x=0 \textrm{ tai } -0,0125x+0,3=0 $]]
[[$\Leftrightarrow x=0 \textrm{ tai } x=\frac{-0,3}{-0,125}=24$]]
Kuvaaja on alaspäin aukeava paraabeli ja sen huippu sijaitsee nollakohtien puolivälissä, eli kohdassa [[$x=12$]]. Pallon korkeus tällöin on [[$y(12)=-0,0125 \cdot 12^2 + 0,3 \cdot 12 = 1,8$]]
Vastaus: Pallo lentää vaakasuunnassa 24 metrin päähän lähtöpaikasta ja käy korkeimmillaan 1,8 m korkeudella.
Esimerkki 6
Kun 120 km matka ajettiin 10 km/h nopeammin kuin aikaisemmin, matka sujui 12 minuuttia nopeammin. Kuinka suuri oli alkuperäinen nopeus?
Ratkaisu:
Merkitään muuttujalla [[$v$]] alkuperäistä nopeutta. Lisätty nopeus on [[$v + 10$]]. Nopeuden yksikkönä on km/h, joten aika muutetaan tunneiksi: [[$ 12 \textrm{ min }=\frac{12}{60} \textrm{ h }=\frac{1}{5} \textrm{ h }$]].
Nyt [[$aika= \frac{matka}{nopeus}$]]. Jätetään yksiköt pois lausekkeista.
Aika ennen on [[$\frac{120 }{v}$]] ja nopeuden noston jälkeen [[$\frac{120}{v+10}$]]. Näiden ero on 12 min, joten saadaan yhtälö:
[[$$ \begin{eqnarray}\frac{120}{v}-\frac{1}{5}&=&\frac{120}{v+10} \quad ||\cdot 5v(v+10) \quad \textrm{kerrotaan kaikki nimittäjät pois} \\ \\ \frac{120 \cdot 5v(v+10)}{v} -\frac{5v(v+10)}{5}&=&\frac{120 \cdot5v(v+10)}{v+10} \quad \textrm{josta nimittäjät supistamalla} \\ \\ 600(v+10)-(v^2+10)&=&600v \\ 600v+6000-v^2-10v&=&600v \\ -v^2-10v+6000&=&0 \end{eqnarray} $$]]
[[$$ \begin{eqnarray} v&=&\frac{-(-10) \pm \sqrt{(-10)^2-4\cdot (-1) \cdot 6000}}{2 \cdot (-1)} \\ \\ &&\textrm{ nyt likiarvot riittävät, joten lasketaan juuren arvo laskimella}\\ \\ v&=&\frac{10 \pm 155,24...}{-2} \textrm{, josta}\\ v&=&\frac{165,25...}{-2}=-82,6... \quad \textrm { tai } v= \frac{-145,25...}{-2}=72,62... \end{eqnarray}$$]]
Näistä negatiivinen ratkaisu pitää hylätä.
Vastaus: Alkuperäinen nopeus matkalla oli 73 km/h.