Seuraavissa esimerkeissä käytännön tilanne johtaa toisen asteen yhtälöön.

Esimerkki 4

Suorakulmion muotoisen tontin pinta-ala on 1260 m² ja ympärysmitta 144 m. Kuinka pitkiä ovat tontin sivut?

Ratkaisu:

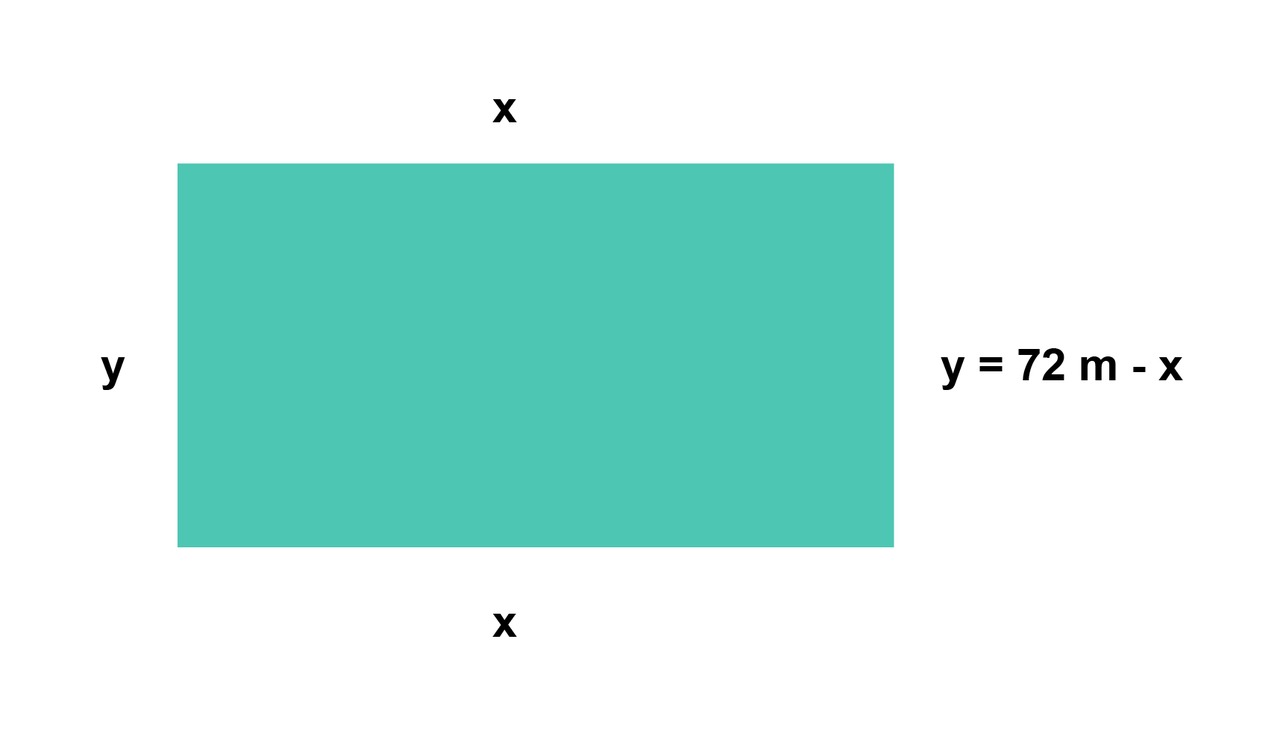
Merkitään vaakasivun pituutta muuttujalla [[$x$]]. Kahden vaakasivun pituus on [[$2x$]]. Pystysuuntaisiin sivuihin jää tällöin yhteensä [[$144-2x$]] metriä. Yksi pystysivu on näin [[$y=\frac{144-2x}{2}$]] metriä, eli sievennettynä [[$y= 72 -x$]] metriä. (Sama voidaan päätellä myös niin, että yksi vaakasivu ja pystysivu ovat yhteensä puolet ympärysmitasta, eli 72 m. Näin [[$x+y=72 \Leftrightarrow y=72-x $]].)
Pinta-ala: [[$x(72-x)=1260$]], josta normaalimuodossa [[$72x-x^2=1260 \Leftrightarrow -x^2+72x-1260=0$]]

Ratkaisukaavalla
[[$$x=\frac{-72 \pm \sqrt{72^2-4 \cdot (-1) \cdot (-1260)}}{2 \cdot (-1)} = \frac{-72 \pm \sqrt{144}}{-2} = \frac{-72 \pm 12}{-2},$$]]
josta saadaan ratkaisut
[[$$x=\frac{-60}{-2}=30 \textrm{ tai } x=\frac{-84}{-2}=42.$$]]

Jos vaakasivun pituus on [[$x=30 \textrm{ m}$]], toinen sivu on [[$72 \textrm{ m} - 30 \textrm{ m}=42 \textrm{ m}$]], joka on juuri toinen yhtälön juuri. Samoin, jos [[$x=42$]], on [[$y=30$]].

Vastaus: Sivujen pituuden ovat 42 metriä ja 30 metriä.

Esimerkki 5

Ilmaan potkaistun pallon lentorata noudatti funktiota [[$y=-0,0125x^2+0,3x$]], missä [[$x$]]-akseli kuvaa maan pintaa ja koordinaatiston yksikkönä on 1 m. Kuinka pitkälle pallo lensi vaakasuunnassa? Kuinka korkealla se kävi?

Ratkaisu:
Pallo on maan pinnalla kuvaajan nollakohdissa.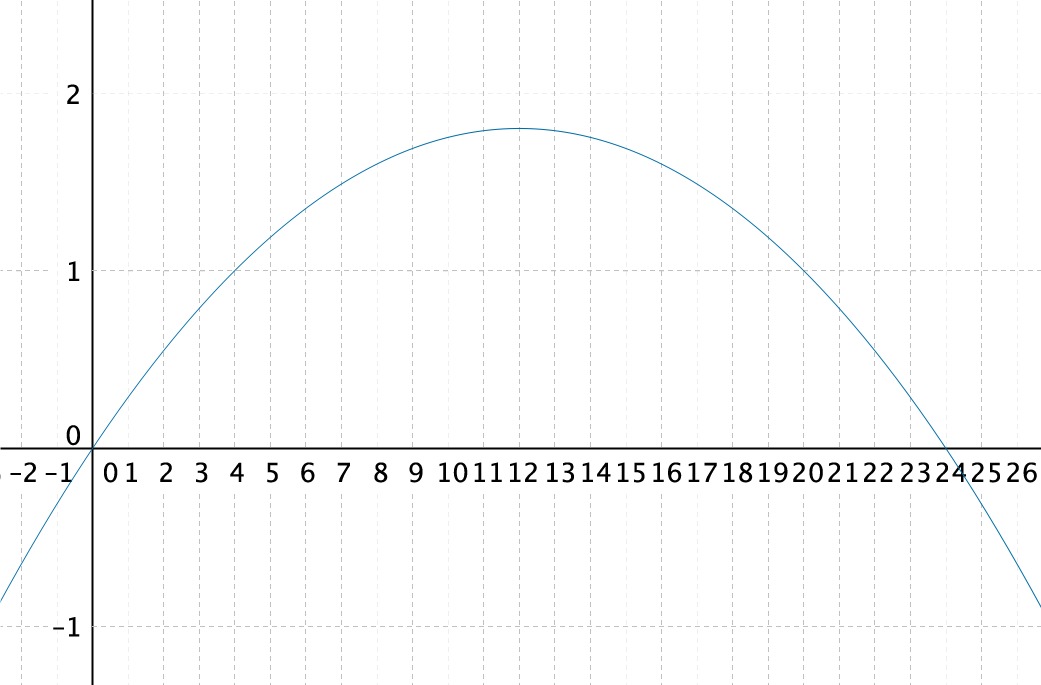

[[$y=0 \Leftrightarrow -0,0125x^2+0.3x=0 \Leftrightarrow x(-0,0125x+0,3)=0 $]]
[[$\Leftrightarrow x=0 \textrm{ tai } -0,0125x+0,3=0 $]]
[[$\Leftrightarrow x=0 \textrm{ tai } x=\frac{-0,3}{-0,125}=24$]]

Kuvaaja on alaspäin aukeava paraabeli ja sen huippu sijaitsee nollakohtien puolivälissä, eli kohdassa [[$x=12$]]. Pallon korkeus tällöin on [[$y(12)=-0,0125 \cdot 12^2 + 0,3 \cdot 12 = 1,8$]]

Vastaus: Pallo lentää vaakasuunnassa 24 metrin päähän lähtöpaikasta ja käy korkeimmillaan 1,8 m korkeudella.

Esimerkki 6

Kun 120 km matka ajettiin 10 km/h nopeammin kuin aikaisemmin, matka sujui 12 minuuttia nopeammin. Kuinka suuri oli alkuperäinen nopeus?

Ratkaisu:
Merkitään muuttujalla [[$v$]] alkuperäistä nopeutta. Lisätty nopeus on [[$v + 10$]]. Nopeuden yksikkönä on km/h, joten aika muutetaan tunneiksi: [[$ 12 \textrm{ min }=\frac{12}{60} \textrm{ h }=\frac{1}{5} \textrm{ h }$]].

Nyt [[$aika= \frac{matka}{nopeus}$]]. Jätetään yksiköt pois lausekkeista.

Aika ennen on [[$\frac{120 }{v}$]] ja nopeuden noston jälkeen [[$\frac{120}{v+10}$]]. Näiden ero on 12 min, joten saadaan yhtälö:
[[$$ \begin{eqnarray}\frac{120}{v}-\frac{1}{5}&=&\frac{120}{v+10} \quad ||\cdot 5v(v+10) \quad \textrm{kerrotaan kaikki nimittäjät pois} \\ \\ \frac{120 \cdot 5v(v+10)}{v} -\frac{5v(v+10)}{5}&=&\frac{120 \cdot5v(v+10)}{v+10} \quad \textrm{josta nimittäjät supistamalla} \\ \\ 600(v+10)-(v^2+10)&=&600v \\ 600v+6000-v^2-10v&=&600v \\ -v^2-10v+6000&=&0 \end{eqnarray} $$]]
[[$$ \begin{eqnarray} v&=&\frac{-(-10) \pm \sqrt{(-10)^2-4\cdot (-1) \cdot 6000}}{2 \cdot (-1)} \\ \\ &&\textrm{ nyt likiarvot riittävät, joten lasketaan juuren arvo laskimella}\\ \\ v&=&\frac{10 \pm 155,24...}{-2} \textrm{, josta}\\ v&=&\frac{165,25...}{-2}=-82,6... \quad \textrm { tai } v= \frac{-145,25...}{-2}=72,62... \end{eqnarray}$$]]
Näistä negatiivinen ratkaisu pitää hylätä.

Vastaus: Alkuperäinen nopeus matkalla oli 73 km/h.