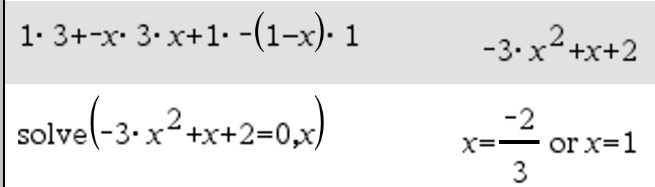3.2 Pistetulo
332
331
a)
suunnikkaan sivuvektorit


b)
suunnikkaan kulmat
%3D%5Cfrac%7B%5Coverline%7Ba%7D%5Ccdot%5Coverline%7Bb%7D%7D%7B%5Cleft%7C%5Coverline%7Ba%7D%5Cright%7C%5Cleft%7C%5Coverline%7Bb%7D%5Cright%7C%7D%3D%5Cfrac%7B8%7D%7B17%7D%3D0%7B%2C%7D4705...)



suunnikkaan sivuvektorit
b)
suunnikkaan kulmat
toinen kulma voidaan laskea
327
tämä kärki ei ole suorakulmainen
selvitetään kolmas sivuvektori ja selvitetään sen avulla, onko kolmion muut kärjet suorakulmaisia
tämä kärki on suorakulmainen
kolmio on suorakulmainen, koska sen samasta kärjestä lähtevien sivuvektorien pistetulo on 0
333
323
a)
vektorit ovat kohtisuorassa toisiaan vastaan
b)
vektorit eivät ole kohtisuorassa toisiaan vastaan
c)
vektorit eivät ole kohtisuorassa toisiaan vastaan
d)
vektorit ovat kohtisuorassa toisiaan vastaan
322
a)
b)
c)
d)
329
kulma A





%3D%5Cfrac%7B17%7D%7B3%5Csqrt%7B85%7D%7D)
%3D52%7B%2C%7D0745...%C2%B0%5Capprox52%7B%2C%7D1%C2%B0)


%2B0%5Ccdot2%3D-12)

%5E2%2B2%5E2%7D%3D2%5Csqrt%7B2%7D)
%3D%5Cfrac%7B-12%7D%7B6%5Ccdot2%5Csqrt%7B2%7D%7D)
%3D135%C2%B0)
kulma C